Graph Neural Networks: A Review of Methods and Applications（图神经网络：方法与应用综述）

Graph Neural Networks: A Review of Methods and Applications

图神经网络：方法与应用综述

Jie Zhou , Ganqu Cui , Zhengyan Zhang , Cheng Yang, Zhiyuan Liu, Lifeng Wang, Changcheng Li, Maosong Sun

Abstract—Lots of learning tasks require dealing with graph data which contains rich relation information among elements. Modeling physics system, learning molecular fingerprints, predicting protein interface, and classifying diseases require that a model learns from graph inputs. In other domains such as learning from non-structural data like texts and images, reasoning on extracted structures, like the dependency tree of sentences and the scene graph of images, is an important research topic which also needs graph reasoning models. Graph neural networks (GNNs) are connectionist models that capture the dependence of graphs via message passing between the nodes of graphs. Unlike standard neural networks, graph neural networks retain a state that can represent information from its neighborhood with arbitrary depth. Although the primitive GNNs have been found difficult to train for a fixed point, recent advances in network architectures, optimization techniques, and parallel computation have enabled successful learning with them. In recent years, systems based on graph convolutional network (GCN) and gated graph neural network (GGNN) have demonstrated ground-breaking performance on many tasks mentioned above. In this survey, we provide a detailed review over existing graph neural network models, systematically categorize the applications, and propose four open problems for future research.

Index Terms—Deep Learning, Graph Neural Network

摘要 - 许多学习任务需要处理包含元素之间丰富关系信息的图形数据。物理系统建模，学习分子指纹，预测蛋白质界面和分类疾病需要模型从图形输入中学习。在其他领域，如从文本和图像等非结构性数据中学习，对提取结构的推理，如句子的依赖树和图像的场景图，是一个重要的研究课题，也需要图形推理模型。图形神经网络（GNN）是连接模型，通过图形节点之间的消息传递捕获图形的依赖性。与标准神经网络不同，图形神经网络保留一种状态，该状态可以表示来自其邻域的任意深度的信息。尽管已发现原始GNN难以针对固定点进行训练，但网络体系结构，优化技术和并行计算的最新进展使得能够成功地学习它们。近年来，基于图卷积网络（GCN）和门控图神经网络（GGNN）的系统已经在上述许多任务中展示了突破性的性能。在本综述中，我们对现有的图形神经网络模型进行了详细的审查，系统地对应用程序进行了分类，并为未来的研究提出了四个未解决的问题。

索引术语 - 深度学习，图形神经网络

1 INTRODUCTION

Graphs are a kind of data structure which models a set of objects (nodes) and their relationships (edges). Recently, researches of analyzing graphs with machine learning have been receiving more and more attention because of the great expressive power of graphs, i.e. graphs can be used as denotation of a large number of systems across various areas including social science (social networks) [1], [2], nat-ural science (physical systems [3], [4] and protein-protein interaction networks [5]), knowledge graphs [6] and many other research areas [7]. As a unique non-Euclidean data structure for machine learning, graph analysis focuses on node classification, link prediction, and clustering. Graph neural networks (GNNs) are deep learning based methods that operate on graph domain. Due to its convincing per-formance and high interpretability, GNN has been a widely applied graph analysis method recently. In the following paragraphs, we will illustrate the fundamental motivations of graph neural networks.

The first motivation of GNNs roots in convolutional neural networks (CNNs) [8]. CNNs have the ability to extract multi-scale localized spatial features and compose them to construct highly expressive representations, which led to breakthroughs in almost all machine learning areas and started the new era of deep learning [9]. However, CNNs can only operate on regular Euclidean data like images (2D grid) and text (1D sequence) while these data structures can be regarded as instances of graphs. As we are going deeper into CNNs and graphs, we found the keys of CNNs: local connection, shared weights and the use of multi-layer [9]. These are also of great importance in solving problems of graph domain, because 1) graphs are the most typical locally connected structure. 2) shared weights reduce the computational cost compared with traditional spectral graph theory [10]. 3) multi-layer structure is the key to deal with hierarchical patterns, which captures the features of various sizes. Therefore, it is straightforward to think of finding the generalization of CNNs to graphs. However, as shown in 1, it is hard to define localized convolutional filters and pooling operators, which hinders the transformation of CNN from Euclidean domain to non-Euclidean domain.
图形是一种数据结构，它模拟一组对象（节点）及其关系（边缘）。近年来，由于图形的强大表现力，用机器学习分析图形的研究越来越受到关注，即图形可以用作包括社会科学（社会网络）在内的各个领域的大量系统的表示[1] ]，[2]，自然科学（物理系统[3]，[4]和蛋白质 - 蛋白质相互作用网络[5]），知识图[6]和许多其他研究领域[7]。作为机器学习的独特的非欧几里德数据结构，图形分析侧重于节点分类，链接预测和聚类。图神经网络（GNN）是基于深度学习的方法，在图域上运行。由于其令人信服的性能和高可解释性，GNN最近已成为一种广泛应用的图形分析方法。在以下段落中，我们将说明图神经网络的基本动机。

GNN的第一个动机源于卷积神经网络（CNN）[8]。 CNN具有提取多尺度局部空间特征的能力，并构建它们以构建高度表达的表征，这导致几乎所有机器学习领域的突破并开始了深度学习的新时代[9]。然而，CNN只能操作规则的欧几里德数据，如图像（2D网格）和文本（1D序列），而这些数据结构可以视为图形的实例。随着我们更深入地了解CNN和图表，我们找到了CNN的密钥：本地连接，共享权重和多层使用[9]。这些对于解决图域的问题也非常重要，因为1）图是最典型的局部连接结构。 2）与传统的谱图理论相比，共享权重降低了计算成本[10]。 3）多层结构是处理分层模式的关键，它捕获各种大小的特征。因此，可以直接考虑找到CNN到图的概括。然而，如图1所示，很难定义局部卷积滤波器和汇集算子，这阻碍了CNN从欧几里德域到非欧几里德域的转换。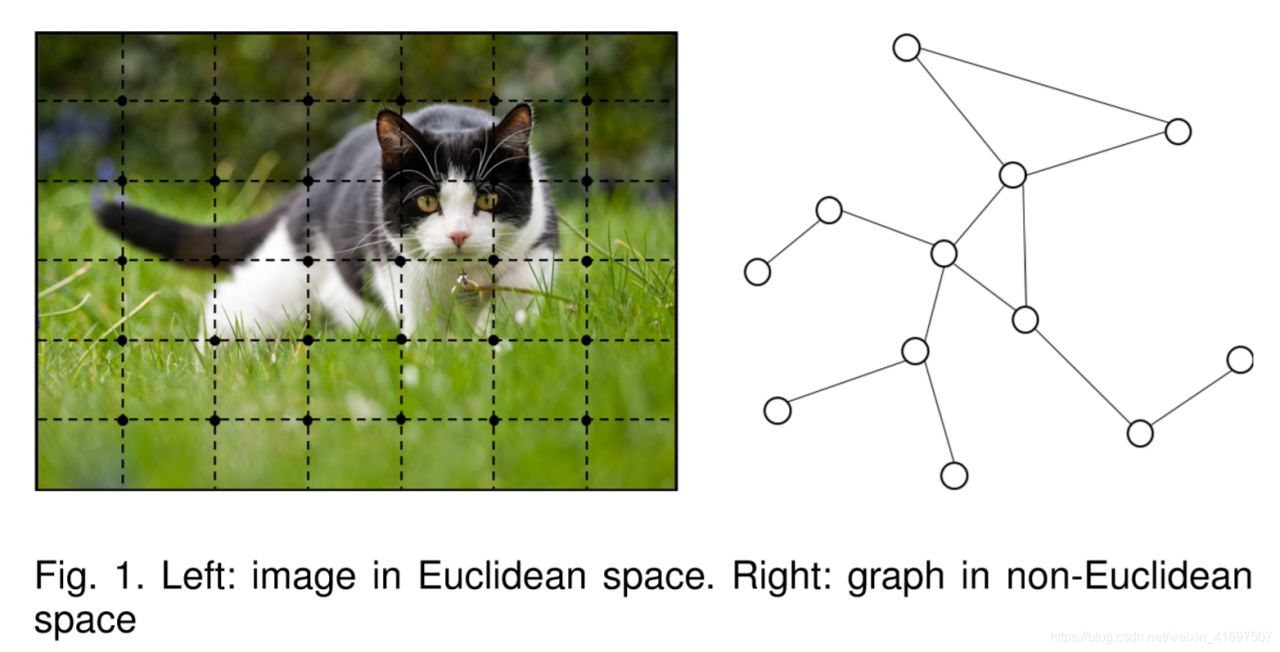

The other motivation comes from graph embedding, which learns to represent graph nodes, edges or subgraphs in low-dimensional vectors. In the field of graph analysis, tradi-tional machine learning approaches usually rely on hand engineered features and are limited by its inflexibility and high cost. Following the idea of representation learning and the success of word embedding [11], DeepWalk [12], which is regarded as the first graph embedding method based on representation learning, applies SkipGram model [11] on the generated random walks. Similar approaches such as node2vec [13], LINE [14] and TADW [15] also achieved breakthroughs. However, these methods suffer two severe drawbacks [16]. First, no parameters are shared between nodes in the encoder, which leads to computationally in-efficiency, since it means the number of parameters grows linearly with the number of nodes. Second, the direct em-bedding methods lack the ability of generalization, which means they cannot deal with dynamic graphs or generalize to new graphs.

Based on CNNs and graph embedding, graph neural networks (GNNs) are proposed to collectively aggregate in-formation from graph structure. Thus they can model input and/or output consisting of elements and their dependency. Further, graph neural network can simultaneously model the diffusion process on the graph with the RNN kernel.

In the following part, we explain the fundamental rea-sons why graph neural networks are worth investigating. Firstly, the standard neural networks like CNNs and RNNs cannot handle the graph input properly in that they stack the feature of nodes by a specific order. However, there isn’t a natural order of nodes in the graph. To present a graph completely, we should traverse all the possible orders as the input of the model like CNNs and RNNs, which is very redundant when computing. To solve this problem, GNNs propagate on each node respectively, ignoring the input order of nodes. In other words, the output of GNNs is invariant for the input order of nodes. Secondly, an edge in a graph represents the information of dependency between two nodes. In the standard neural networks, the dependency information is just regarded as the feature of nodes. However, GNNs can do propagation guided by the graph structure instead of using it as part of features. Generally, GNNs update the hidden state of nodes by a weighted sum of the states of their neighborhood. Thirdly, reasoning is a very important research topic for high-level artificial intelligence and the reasoning process in human brain is almost based on the graph which is extracted from daily experience. The standard neural networks have shown the ability to generate synthetic images and documents by learning the distribution of data while they still cannot learn the reasoning graph from large experimental data. However, GNNs explore to generate the graph from non-structural data like scene pictures and story documents, which can be a powerful neural model for further high-level AI. Recently, it has been proved that an untrained GNN with a simple architecture also perform well [17].
另一个动机来自图形嵌入，它学习表示低维向量中的图形节点，边或子图。在图形分析领域，传统的机器学习方法通​​常依赖于手工设计的特征，并且受到其不灵活性和高成本的限制。根据表示学习的思想和单词嵌入的成功[11]，DeepWalk [12]被认为是第一种基于表示学习的图嵌入方法，将SkipGram模型[11]应用于生成的随机游走。类似的方法，如node2vec [13]，LINE [14]和TADW [15]也取得了突破。然而，这些方法有两个严重的缺点[16]。首先，编码器中的节点之间不共享参数，这导致计算效率低，因为这意味着参数的数量随着节点的数量线性增长。其次，直接嵌入方法缺乏泛化能力，这意味着它们无法处理动态图形或推广到新图形。

基于CNN和图形嵌入，提出了图形神经网络（GNN）来从图形结构中共同聚合信息。因此，他们可以模拟由元素及其依赖性组成的输入和/或输出。此外，图神经网络可以使用RNN内核同时对图上的扩散过程进行建模。

在下面的部分中，我们将解释为什么图神经网络值得研究的基本原理。首先，像CNN和RNN这样的标准神经网络无法正确处理图形输入，因为它们按特定顺序堆叠节点的特征。但是，图中没有自然的节点顺序。为了完整地呈现图形，我们应该遍历所有可能的顺序作为模型的输入，如CNN和RNN，这在计算时非常冗余。为了解决这个问题，GNN分别在每个节点上传播，忽略了节点的输入顺序。换句话说，GNN的输出对于节点的输入顺序是不变的。其次，图中的边表示两个节点之间的依赖关系的信息。在标准神经网络中，依赖信息仅被视为节点的特征。但是，GNN可以通过图形结构进行传播，而不是将其用作要素的一部分。通常，GNN通过其邻域的状态的加权和来更新节点的隐藏状态。第三，推理是高级人工智能的一个非常重要的研究课题，人脑中的推理过程几乎都是基于从日常经验中提取的图形。标准神经网络已经显示出通过学习数据分布来生成合成图像和文档的能力，同时它们仍然无法从大型实验数据中学习推理图。然而，GNN探索从场景图片和故事文档等非结构性数据生成图形，这可以成为进一步高级AI的强大神经模型。最近，已经证明，具有简单架构的未经训练的GNN也表现良好[17]。
There exist several comprehensive reviews on graph neural networks. [18] gives a formal definition of early graph neural network approaches. And [19] demonstrates the approximation properties and computational capabil-ities of graph neural networks. [20] proposed a unified framework, MoNet, to generalize CNN architectures to non-Euclidean domains (graphs and manifolds) and the framework could generalize several spectral methods on graphs [2], [21] as well as some models on manifolds [22],

[23].[24] provides a thorough review of geometric deep learning, which presents its problems, difficulties, solutions, applications and future directions. [20] and [24] focus on generalizing convolutions to graphs or manifolds, how-ever in this paper we only focus on problems defined on graphs and we also investigate other mechanisms used in graph neural networks such as gate mechanism, attention mechanism and skip connection. [25] proposed the message passing neural network (MPNN) which could generalize several graph neural network and graph convolutional net-work approaches. It presents the definition of the message passing neural network and demonstrates its application on quantum chemistry. [26] proposed the non-local neural net-work (NLNN) which unifies several “self-attention”-style methods. However, the model is not explicitly defined on graphs in the original paper. Focusing on specific applica-tion domains, [25] and [26] only give examples of how to generalize other models using their framework and they do not provide a review over other graph neural network models. [27] proposed the graph network (GN) framework. The framework has a strong capability to generalize other models and its relational inductive biases promote combi-natorial generalization, which is thought to be a top priority for AI. However, [27] is part position paper, part review and part unification and it only gives a rough classification of the applications. In this paper, we provide a thorough review of different graph neural network models as well as a systematic taxonomy of the applications.

To summarize, this paper presents an extensive survey of graph neural networks with the following contributions.

We provide a detailed review over existing graph neural network models. We introduce the original model, its variants and several general frameworks. We examine various models in this area and provide a unified representation to present different propaga-tion steps in different models. One can easily make a distinction between different models using our repre-sentation by recognizing corresponding aggregators and updaters.

We systematically categorize the applications and divide the applications into structural scenarios, non-structural scenarios and other scenarios. We present several major applications and their corresponding methods in different scenarios.
关于图神经网络存在若干综合评论。 [18]给出了早期图神经网络方法的正式定义。 [19]展示了图神经网络的近似性质和计算能力。 [20]提出了一个统一的框架，MoNet，将CNN架构推广到非欧几里得域（图和流形），框架可以推广图上的几种谱方法[2]，[21]以及流形上的一些模型[22] ]

[23]。[24]提供了几何深度学习的全面回顾，提出了它的问题，困难，解决方案，应用和未来方向。 [20]和[24]侧重于将卷积推广到图形或流形，然而在本文中我们只关注图形上定义的问题，我们还研究了图形神经网络中使用的其他机制，如门机制，注意机制和跳过连接。 [25]提出了消息传递神经网络（MPNN），它可以推广几种图形神经网络和图形卷积网络方法。它介绍了通过神经网络的消息的定义，并展示了它在量子化学中的应用。 [26]提出了非局部神经网络（NLNN），它统一了几种“自我关注”式的方法。但是，该模型未在原始论文的图表中明确定义。关注特定的应用领域，[25]和[26]仅举例说明如何使用其框架推广其他模型，并且他们不提供对其他图神经网络模型的评论。 [27]提出了图形网络（GN）框架。该框架具有很强的推广其他模型的能力，其关系归纳偏差促进了组合概括，这被认为是人工智能的首要任务。然而，[27]是部分立场文件，部分审查和部分统一，它只给出了应用程序的粗略分类。在本文中，我们提供了对不同图形神经网络模型的全面回顾以及应用程序的系统分类。

总之，本文对图神经网络进行了广泛的研究，并做出了以下贡献。

我们提供了对现有图神经网络模型的详细评论。我们介绍了原始模型，其变体和几个通用框架。我们研究了该领域的各种模型，并提供了统一的表示，以在不同的模型中呈现不同的传播步骤。通过识别相应的聚合器和更新器，可以使用我们的表示轻松区分不同的模型。

我们系统地对应用程序进行分类，并将应用程序划分为结构场景，非结构场景和其他场景。我们在不同场景中介绍了几个主要应用及其相应的方法。
We propose four open problems for future research. Graph neural networks suffer from over-smoothing and scaling problems. There are still no effective methods for dealing with dynamic graphs as well as modeling non-structural sensory data. We provide a thorough analysis of each problem and propose future research directions.

The rest of this survey is organized as follows. In Sec. 2, we introduce various models in the graph neural network family. We first introduce the original framework and its limitations. And then we present its variants that try to release the limitations. And finally, we introduce several general frameworks proposed recently. In Sec. 3, we will in-troduce several major applications of graph neural networks applied to structural scenarios, non-structural scenarios and other scenarios. In Sec. 4, we propose four open problems of graph neural networks as well as several future research directions. And finally, we conclude the survey in Sec. 5.
我们为未来的研究提出四个未解决的问题 图神经网络遭受过度平滑和缩放问题。 仍然没有有效的方法来处理动态图以及建模非结构感觉数据。 我们对每个问题进行全面分析，并提出未来的研究方向。

本调查的其余部分安排如下。 在第二节 2，我们在图神经网络家族中介绍各种模型。 我们首先介绍原始框架及其局限性。 然后我们展示了试图释放限制的变体。 最后，我们介绍了最近提出的几个一般框架。 在第二节 3，我们将介绍应用于结构场景，非结构场景和其他场景的图神经网络的几个主要应用。 在第二节 4，我们提出了图神经网络的四个开放问题以及未来的几个研究方向。 最后，我们在第二节结束调查。5。

2 MODELS

Graph neural networks are useful tools on non-Euclidean structures and there are various methods proposed in the literature trying to improve the model’s capability.
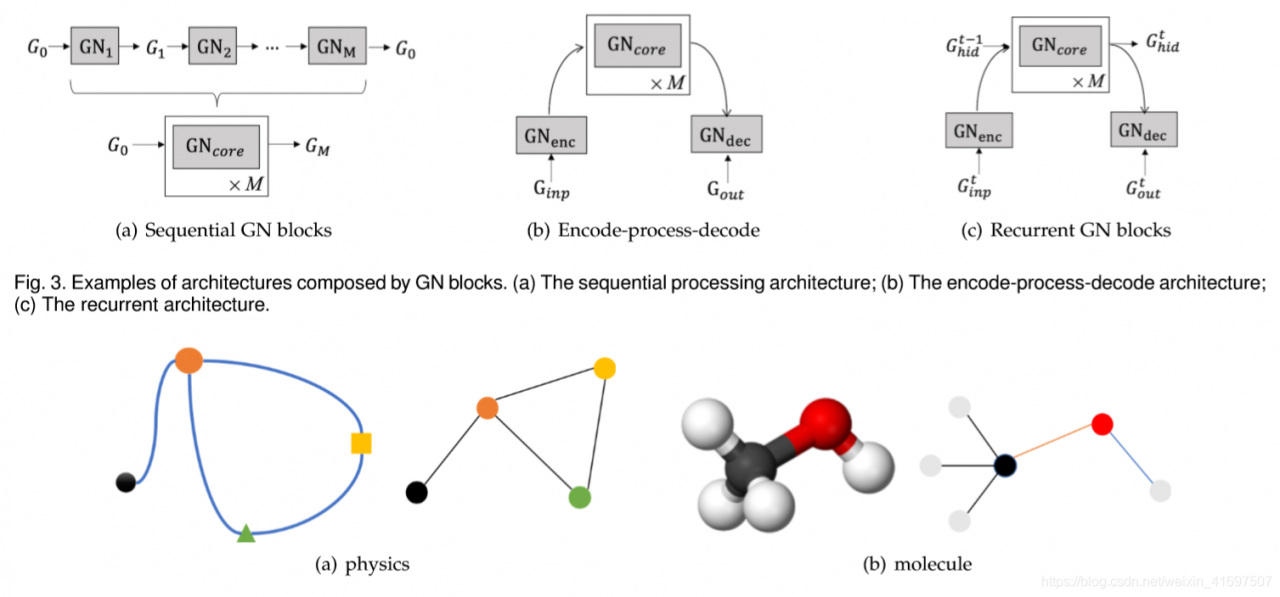
In Sec 2.1, we describe the original graph neural net-works proposed in [18]. We also list the limitations of the original GNN in representation capability and train-ing efficiency. In Sec 2.2 we introduce several variants of graph neural networks aiming to release the limitations. These variants operate on graphs with different types, uti-lize different propagation functions and advanced training methods. In Sec 2.3 we present three general frameworks which could generalize and extend several lines of work. In detail, the message passing neural network (MPNN) [25] unifies various graph neural network and graph convolu-tional network approaches; the non-local neural network (NLNN) [26] unifies several “self-attention”-style methods. And the graph network(GN) [27] could generalize almost every graph neural network variants mentioned in this paper.
Before going further into different sections, we give the notations that will be used throughout the paper. The detailed descriptions of the notations could be found in Table 1.
图形神经网络是非欧几里德结构的有用工具，文献中提出了各种方法，试图提高模型的能力。
在2.1节中，我们描述了[18]中提出的原始图神经网络。我们还列出了原始GNN在表示能力和训练效率方面的局限性。在第2.2节中，我们介绍了旨在释放限制的图神经网络的几种变体。这些变体在不同类型的图形上运行，利用不同的传播函数和高级训练方法。在第2.3节中，我们提出了三个总体框架，可以概括和扩展几个工作线。详细地说，消息传递神经网络（MPNN）[25]统一了各种图形神经网络和图形卷积网络方法;非局部神经网络（NLNN）[26]统一了几种“自我关注”式的方法。图形网络（GN）[27]可以概括本文中提到的几乎所有图形神经网络变体。
在进一步分为不同部分之前，我们给出将在整篇论文中使用的符号。表1的详细描述见表1。

2.1 Graph Neural Networks

The concept of graph neural network (GNN) was first proposed in [18], which extended existing neural networks for processing the data represented in graph domains. In a graph, each node is naturally defined by its features and the related nodes. The target of GNN is to learn a state embedding hv 2 Rs which contains the information of neighborhood for each node. The state embedding hv is an s-dimension vector of node v and can be used to produce an output ov such as the node label. Let f be a parametric function, called local transition function, that is shared among all nodes and updates the node state according to the input neighborhood. And let g be the local output function that describes how the output is produced. Then, hv and ov are defined as follows:
图神经网络（GNN）的概念最初是在[18]中提出的，它扩展了现有的神经网络，用于处理图域中表示的数据。 在图中，每个节点由其特征和相关节点自然定义。 GNN的目标是学习嵌入hv 2 Rs的状态，其包含每个节点的邻域信息。 状态嵌入hv是节点v的s维向量，并且可以用于产生输出ov，例如节点标签。 设f是一个称为局部转移函数的参数函数，它在所有节点之间共享，并根据输入邻域更新节点状态。 让g成为描述输出产生方式的本地输出函数。 然后，hv和ov定义如下：

all the node features, respectively. Then we have a compact form as:

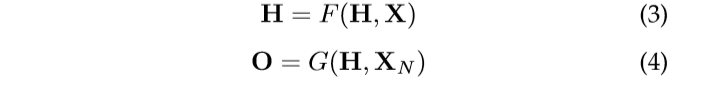
where F , the global transition function, and G, the global output function are stacked versions of f and g for all nodes in a graph, respectively. The value of H is the fixed point of Eq. 3 and is uniquely defined with the assumption that F is a contraction map.

With the suggestion of Banach’s fixed point theorem [28], GNN uses the following classic iterative scheme for computing the state:
其中F，全局转换函数和G，全局输出函数分别是图中所有节点的f和g的堆叠版本。 H的值是Eq的固定点。 在图3中，并且假设F是收缩图而唯一地定义。

根据Banach的不动点定理[28]的建议，GNN使用以下经典迭代方案来计算状态：

where p is the number of supervised nodes. The learning algorithm is based on a gradient-descent strategy and is composed of the following steps.
其中p是受监督节点的数量。 学习算法基于梯度下降策略，并由以下步骤组成。

Limitations Though experimental results showed that GNN is a powerful architecture for modeling structural data, there are still several limitations of the original GNN. Firstly, it is inefficient to update the hidden states of nodes iteratively for the fixed point. If relaxing the assumption of the fixed point, we can design a multi-layer GNN to get a stable representation of node and its neighborhood. Secondly, GNN uses the same parameters in the iteration while most popular neural networks use different parame-ters in different layers, which serve as a hierarchical feature extraction method. Moreover, the update of node hidden states is a sequential process which can benefit from the RNN kernel like GRU and LSTM. Thirdly, there are also some informative features on the edges which cannot be effectively modeled in the original GNN. For example, the edges in the knowledge graph have the type of relations and the message propagation through different edges should be different according to their types. Besides, how to learn the hidden states of edges is also an important problem. Lastly, it is unsuitable to use the fixed points if we focus on the representation of nodes instead of graphs because the distribution of representation in the fixed point will be much smooth in value and less informative for distinguishing each node.
局限性尽管实验结果表明GNN是一种用于建模结构数据的强大架构，但原始GNN仍然存在一些局限性。首先，针对固定点迭代地更新节点的隐藏状态是低效的。如果放宽固定点的假设，我们可以设计一个多层GNN来获得节点及其邻域的稳定表示。其次，GNN在迭代中使用相同的参数，而大多数流行的神经网络在不同的层中使用不同的参数，这些参数用作分层特征提取方法。此外，节点隐藏状态的更新是一个顺序过程，可以受益于RNN内核，如GRU和LSTM。第三，在边缘上也存在一些信息特征，这些特征在原始GNN中无法有效建模。例如，知识图中的边缘具有关系类型，并且通过不同边缘的消息传播应根据其类型而不同。此外，如何学习边缘的隐藏状态也是一个重要问题。最后，如果我们专注于节点的表示而不是图形，则不适合使用固定点，因为固定点中的表示分布将在值上非常平滑并且用于区分每个节点的信息量较少。

2.2 Variants of Graph Neural Networks

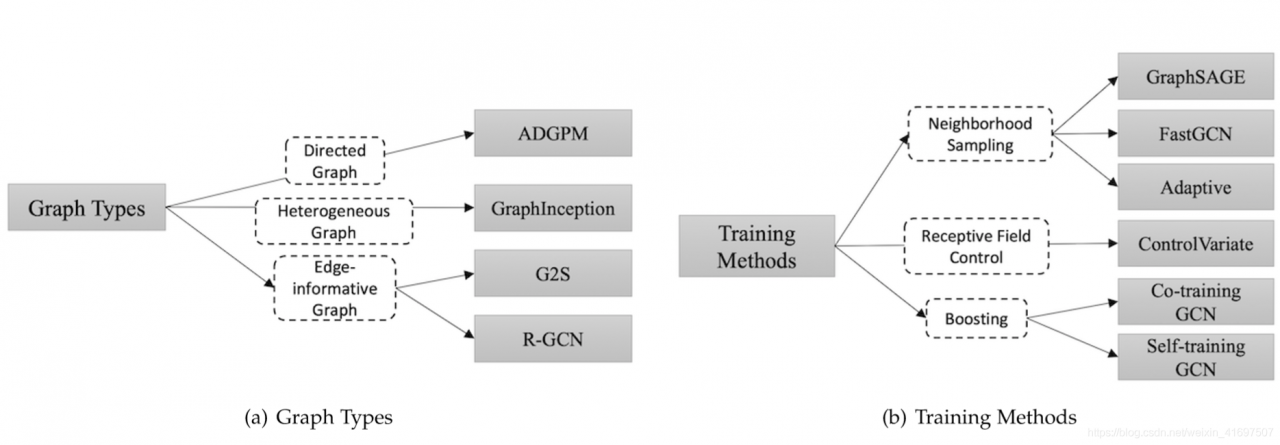
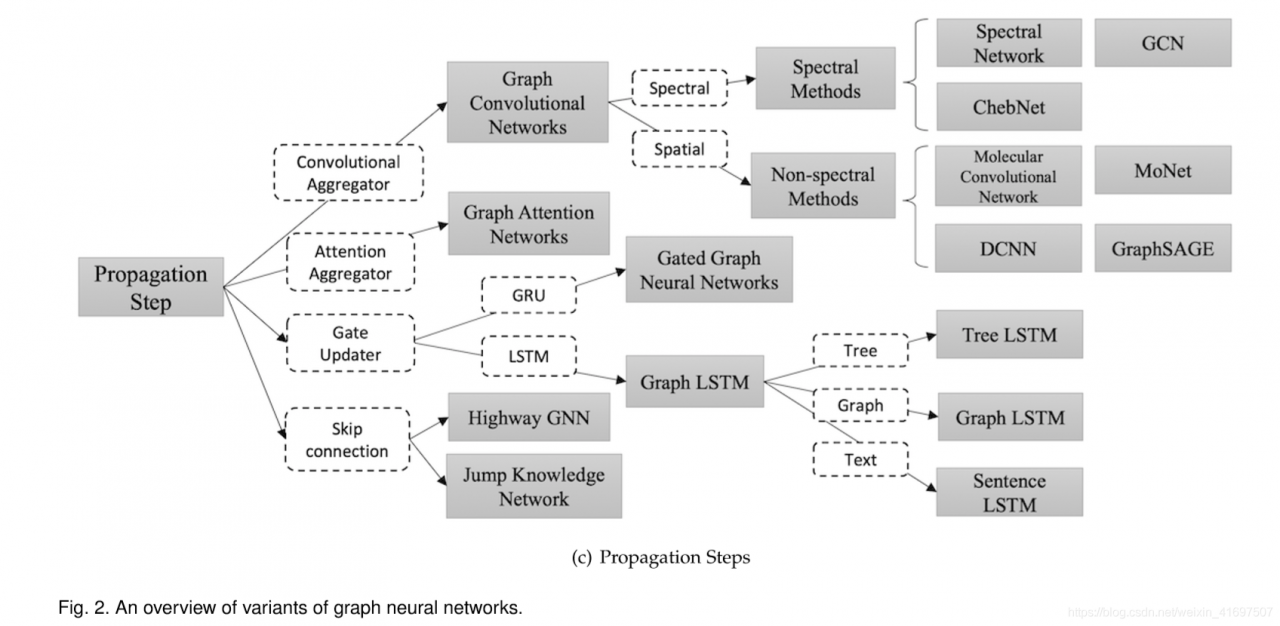
In this subsection, we present several variants of graph neural networks. Sec 2.2.1 focuses on variants operating on different graph types. These variants extend the rep-resentation capability of the original model. Sec 2.2.2 lists several modifications (convolution, gate mechanism, atten-tion mechanism and skip connection) on the propagation step and these models could learn representations with higher quality. Sec 2.2.3 describes variants using advanced training methods, which improve the training efficiency. An overview of different variants of graph neural networks could be found in Fig. 2.
在本小节中，我们提出了图神经网络的几种变体。 Sec 2.2.1侧重于在不同图表类型上运行的变体。 这些变体扩展了原始模型的代表能力。 第2.2.2节列出了传播步骤的几种修改（卷积，门机制，注意机制和跳过连接），这些模型可以学习更高质量的表示。 Sec 2.2.3描述了使用高级培训方法的变体，这些方法提高了培训效率。 可以在图2中找到图神经网络的不同变体的概述。

2.2.1 Graph Types

In the original GNN [18], the input graph consists of nodes with label information and undirected edges, which is the simplest graph format. However, there are many variants of graph in the world. In this subsection, we will introduce some methods designed to model different kinds of graphs.

Directed Graphs The first variant of graph is directed graph. Undirected edge which can be treated as two directed edges shows that there is a relation between two nodes. However, directed edges can bring more information than undirected edges. For example, in a knowledge graph where the edge starts from the head entity and ends at the tail entity, the head entity is the parent class of the tail entity, which suggests we should treat the information propagation process from parent classes and child classes differently. ADGPM [29] uses two kinds of weight matrix, Wp and Wc, to incorporate more precise structural information. The propagation rule is shown as follows:
在原始的GNN [18]中，输入图由具有标签信息和无向边的节点组成，这是最简单的图形格式。 但是，世界上有许多图形变体。 在本小节中，我们将介绍一些用于模拟不同类型图形的方法。

有向图图形的第一个变量是有向图。 可被视为两个有向边的无向边显示两个节点之间存在关系。 但是，有向边可以带来比无向边更多的信息。 例如，在知识图中，边缘从头部实体开始并在尾部实体处结束，头部实体是尾部实体的父类，这表明我们应该以不同的方式处理来自父类和子类的信息传播过程。。 ADGPM [29]使用两种权重矩阵Wp和Wc来合并更精确的结构信息。 传播规则如下所示：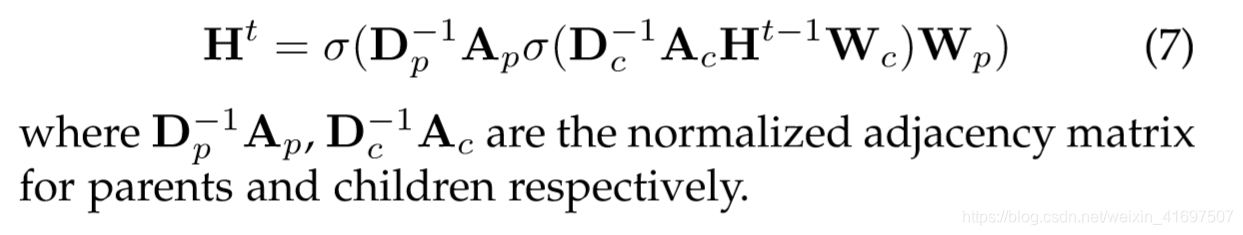

Heterogeneous Graphs The second variant of graph is heterogeneous graph, where there are several kinds of nodes. The simplest way to process heterogeneous graph is to convert the type of each node to a one-hot feature vector which is concatenated with the original feature. What’s more, GraphInception [30] introduces the concept of metapath into the propagation on the heterogeneous graph. With metapath, we can group the neighbors according to their node types and distances. For each neighbor group, GraphInception treats it as a sub-graph in a homogeneous graph to do propagation and concatenates the propagation results from different homogeneous graphs to do a collective node representation.

Graphs with Edge Information In the final variant of graph, each edge also has its information like the weight or the type of the edge. There are two ways to handle this kind of graphs: Firstly, we can convert the graph to a bipartite graph where the original edges also become nodes and one original edge is split into two new edges which means there are two new edges between the edge node and begin/end nodes. The encoder of G2S [31] uses the following aggregation function for neighbors:
异构图图形的第二种变体是异构图，其中有几种节点。处理异构图的最简单方法是将每个节点的类型转换为与原始特征连接的单热特征向量。更重要的是，GraphInception [30]将元路径的概念引入到异构图上的传播中。使用metapath，我们可以根据节点类型和距离对邻居进行分组。对于每个邻居组，GraphInception将其视为同构图中的子图，以进行传播并连接来自不同同构图的传播结果，以进行集合节点表示。

带边缘信息的图形在图形的最终变体中，每条边缘也有其重量或边缘类型等信息。有两种方法可以处理这种图形：首先，我们可以将图形转换为二分图，其中原始边缘也成为节点，一个原始边缘被分成两个新边缘，这意味着边缘节点之间有两个新边缘和开始/结束节点。 G2S [31]的编码器对邻居使用以下聚合函数：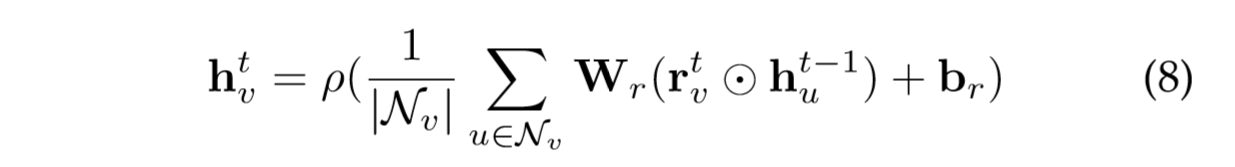

2.2.2 Propagation Types

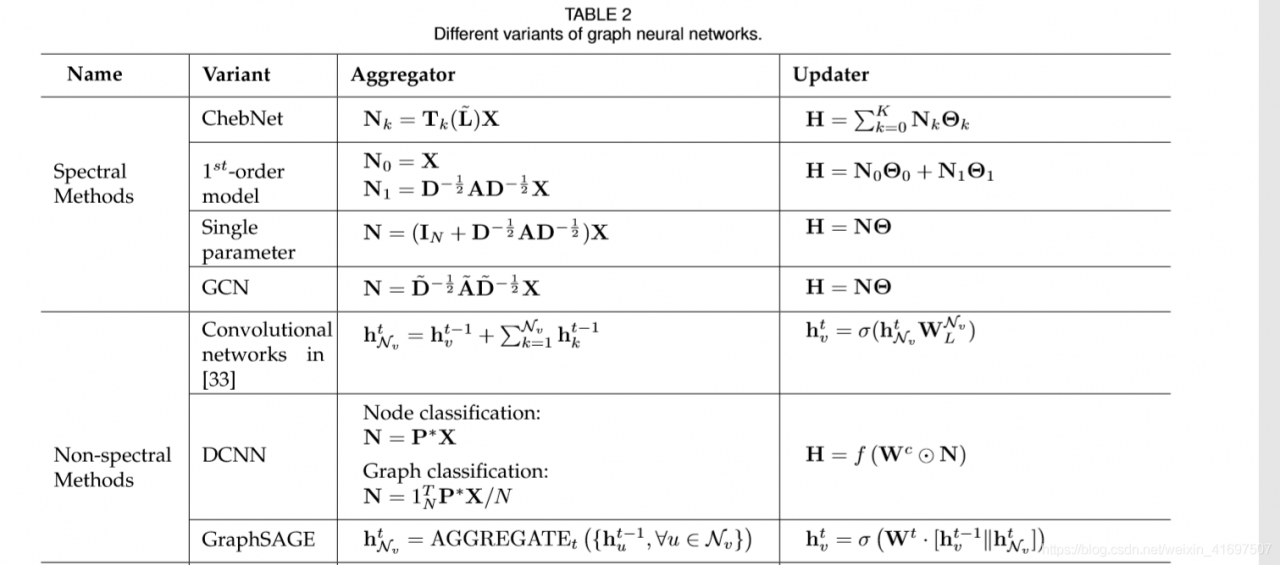
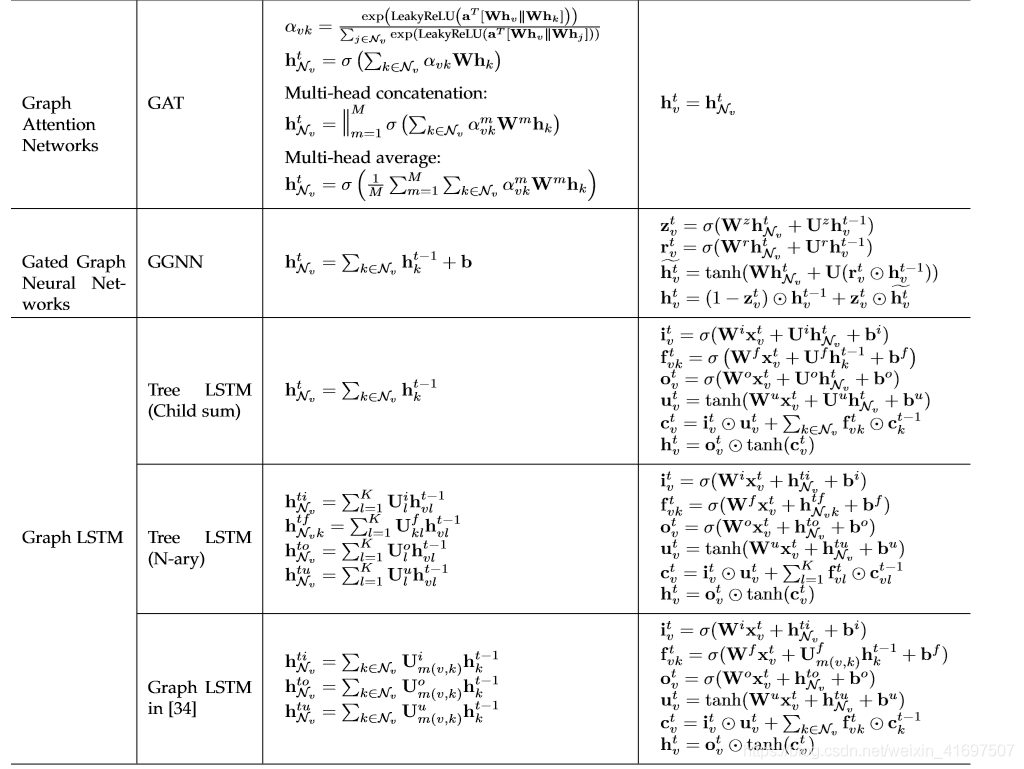
The propagation step and output step are of vital importance in the model to obtain the hidden states of nodes (or edges). As we list below, there are several major modifications in the propagation step from the original graph neural network model while researchers usually follow a simple feed-forward neural network setting in the output step. The comparison of different variants of GNN could be found in Table 2. The variants utilize different aggregators to gather information from each node’s neighbors and specific updaters to update nodes’ hidden states. Convolution. There is an increasing interest in generalizing convolutions to the graph domain. Advances in this direction are often categorized as spectral approaches and non-spectral approaches.
传播步骤和输出步骤在模型中至关重要，以获得节点（或边缘）的隐藏状态。 正如我们在下面列出的那样，在原始图神经网络模型的传播步骤中有几个主要的修改，而研究人员通常在输出步骤中遵循简单的前馈神经网络设置。 GNN的不同变体的比较可以在表2中找到。变体利用不同的聚合器来从每个节点的邻居和特定更新器收集信息以更新节点的隐藏状态。 卷积。 人们越来越关注将卷积推广到图域。 这方面的进展通常被分类为光谱方法和非光谱方法。

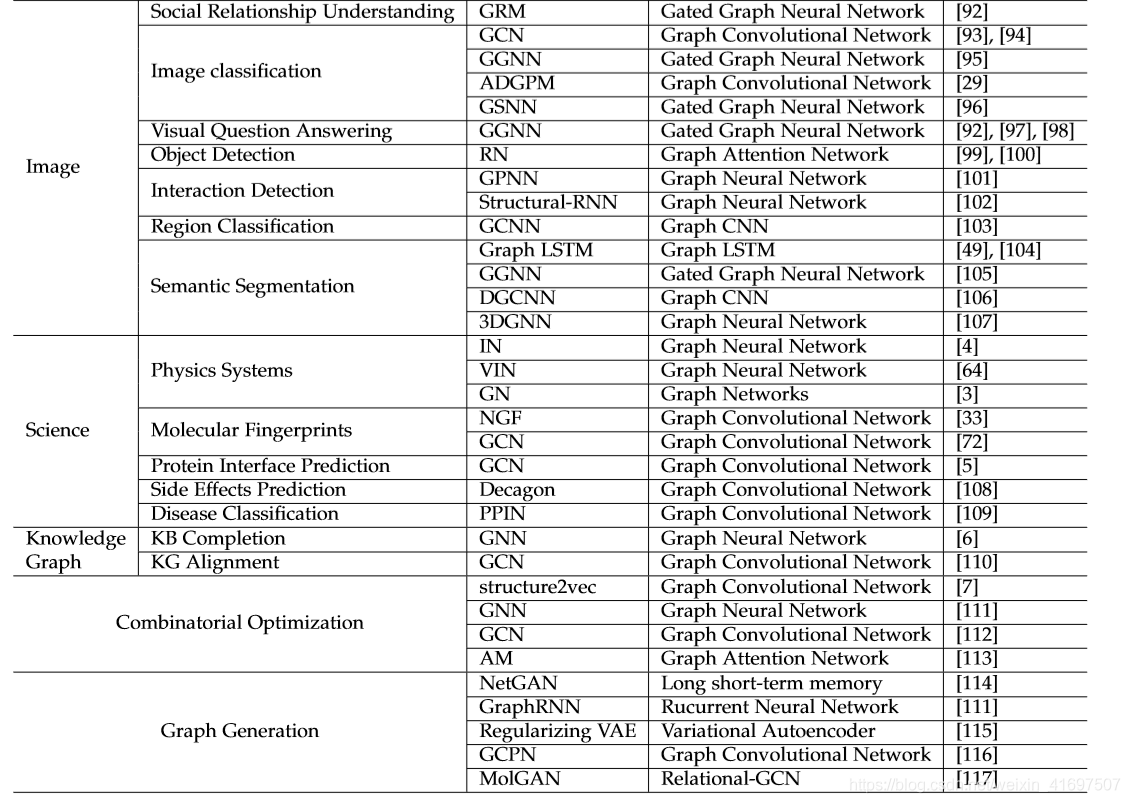
3 APPLICATIONS

Graph neural networks have been explored in a wide range of problem domains across supervised, semi-supervised, unsupervised and reinforcement learning settings. In this section, we simply divide the applications in three scenarios:

(1)Structural scenarios where the data has explicit relational structure, such as physical systems, molecular structure and knowledge graphs; (2) Non-structural scenarios where the relational structure is not explicit include image, text, etc; (3) Other application scenarios such as generative models and combinatorial optimization problems. Note that we only list several representative applications instead of providing an exhaustive list. The summary of the applications could be found in Table 3.
图形神经网络已经在监督，半监督，无监督和强化学习设置的广泛问题领域中进行了探索。 在本节中，我们简单地将应用程序划分为三种情况：

（1）数据具有明确关系结构的结构场景，如物理系统，分子结构和知识图; （2）关系结构不明确的非结构场景包括图像，文本等; （3）其他应用场景，如生成模型和组合优化问题。 请注意，我们仅列出几个有代表性的应用程序，而不是提供详尽的列表。 申请摘要见表3。

3.1 Structural Scenarios

In the following subsections, we will introduce GNN’s applications in structural scenarios, where the data are natu-rally performed in the graph structure. For example, GNNs are widely being used in social network prediction [1], [2], traffic prediction [56], [118], recommender systems [119],

[120]and graph representation [121]. Specifically, we are discussing how to model real-world physical systems with object-relationship graphs, how to predict chemical prop-erties of molecules and biological interaction properties of proteins and the methods of reasoning about the out-of-knowledge-base(OOKB) entities in knowledge graphs.
在以下小节中，我们将在结构场景中介绍GNN的应用程序，其中数据在图结构中自然执行。 例如，GNN广泛用于社交网络预测[1]，[2]，流量预测[56]，[118]，推荐系统[119]，

[120]和图表[121]。 具体来说，我们正在讨论如何使用对象关系图来模拟现实世界的物理系统，如何预测分子的化学特性和蛋白质的生物相互作用特性以及推断知识基础的推理方法（OOKB） 知识图中的实体。

3.1.1 Physics

Modeling real-world physical systems is one of the most basic aspects of understanding human intelligence. By rep-resenting objects as nodes and relations as edges, we can perform GNN-based reasoning about objects, relations, and physics in a simplified but effective way.

[4]proposed Interaction Networks to make predictions and inferences about various physical systems. The model takes objects and relations as input, reasons about their interactions, and applies the effects and physical dynamics to predict new states. They separately model relation-centric and object-centric models, making it easier to generalize across different systems.

Visual Interaction Networks [64] could make predictions from pixels. It learns a state code from two consecutive input frames for each object. Then, after adding their interaction effect by an Interaction Net block, the state decoder converts state codes to next step’s state.

[3]proposed a Graph Network based model which could either perform state prediction or inductive inference. The inference model takes partially observed information as input and constructs a hidden graph for implicit system classification.
对现实世界的物理系统进行建模是理解人类智能的最基本方面之一。通过将对象重新表示为节点和关系作为边缘，我们可以以简化但有效的方式执行关于对象，关系和物理的基于GNN的推理。

[4]提出了交互网络来预测和推断各种物理系统。该模型将对象和关系作为输入，关于它们的相互作用的原因，并应用效果和物理动力学来预测新状态。它们分别建模以关系为中心和以对象为中心的模型，使得更容易在不同系统中进行推广。

视觉交互网络[64]可以从像素进行预测。它从每个对象的两个连续输入帧中学习状态代码。然后，在通过交互网块添加其交互效果之后，状态解码器将状态代码转换为下一步的状态。

[3]提出了一种基于图形网络的模型，它可以执行状态预测或归纳推理。推理模型将部分观察到的信息作为输入，并构造隐式系统分类的隐藏图。

3.1.2 Chemistry and Biology

Molecular Fingerprints Calculating molecular fingerprints, which means feature vectors that represent moleculars, is a core step in computer-aided drug design. Conventional molecular fingerprints are hand-made and fixed. By ap-plying GNN to molecular graphs, we can obtain better fingerprints.

[33]proposed neural graph fingerprints which calculate sub-structure feature vectors via GCN and sum to get overall representation. The aggregation function is
分子指纹计算分子指纹，即代表分子的特征向量，是计算机辅助药物设计的核心步骤。 传统的分子指纹是手工制作和固定的。 通过将GNN应用于分子图，我们可以获得更好的指纹。

[33]提出了神经图指纹，它通过GCN计算子结构特征向量并求和得到整体表示。 聚合功能是

Protein Interface Prediction [5] focused on the task named protein interface prediction, which is a challenging problem with important applications in drug discovery and design. The proposed GCN based method respectively
蛋白质界面预测[5]侧重于蛋白质界面预测的任务，这是一个具有挑战性的问题，在药物发现和设计中具有重要的应用。 分别提出了基于GCN的方法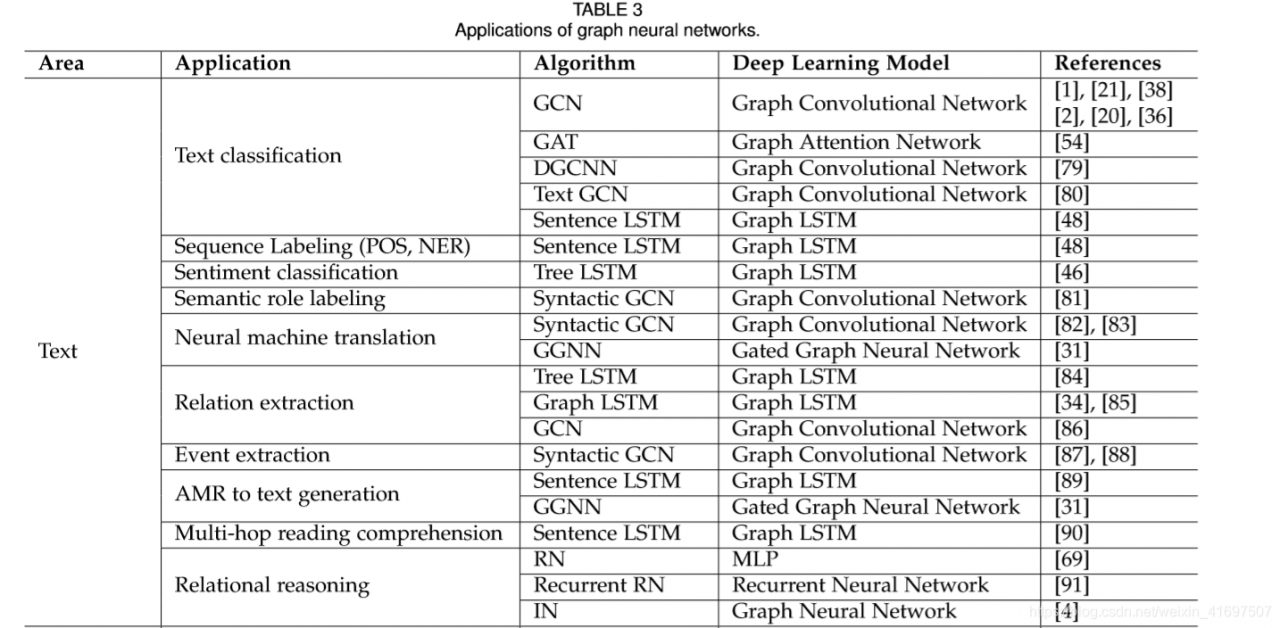

learns ligand and receptor protein residue representation and merges them for pairwise classification.

GNN can also be used in biomedical engineering. With Protein-Protein Interaction Network, [109] leverages graph convolution and relation network for breast cancer subtype classification. [108] also suggests a GCN based model for polypharmacy side effects prediction. Their work models the drug and protein interaction network and separately deals with edges in different types.

学习配体和受体蛋白残基表示并将它们合并用于成对分类。

GNN也可用于生物医学工程。 通过蛋白质 - 蛋白质相互作用网络，[109]利用图卷积和关系网络进行乳腺癌亚型分类。 [108]也提出了基于GCN的多种药物副作用预测模型。 他们的工作模拟了药物和蛋白质相互作用网络，并分别处理不同类型的边缘。

3.1.3 Knowledge graph

[6]utilizes GNNs to solve the out-of-knowledge-base (OOKB) entity problem in knowledge base completion (KBC). The OOKB entities in [6] are directly connected to the existing entities thus the embeddings of OOKB entities can be aggregated from the existing entities. The method achieves satisfying performance both in the standard KBC setting and the OOKB setting.

[110]utilizes GCNs to solve the cross-lingual knowledge graph alignment problem. The model embeds entities from different languages into a unified embedding space and aligns them based on the embedding similarity.
[6]利用GNN来解决知识库完成（KBC）中的知识库外（OOKB）实体问题。 [6]中的OOKB实体直接连接到现有实体，因此可以从现有实体聚合OOKB实体的嵌入。 该方法在标准KBC设置和OOKB设置中都实现了令人满意的性能。

[110]利用GCN来解决跨语言知识图对齐问题。 该模型将来自不同语言的实体嵌入到统一的嵌入空间中，并根据嵌入相似性对齐它们。

3.2 Non-structural Scenarios

In this section we will talk about applications on non-structural scenarios such as image, text, programming source code [45], [122] and multi-agent systems [63], [66],

[76].We will only give detailed introduction to the first two scenarios due to the length limit. Roughly, there are two ways to apply the graph neural networks on non-structural scenarios: (1) Incorporate structural information from other domains to improve the performance, for example using in-formation from knowledge graphs to alleviate the zero-shot problems in image tasks; (2) Infer or assume the relational structure in the scenario and then apply the model to solve the problems defined on graphs, such as the method in [48] which models text into graphs.
在本节中，我们将讨论非结构场景的应用，如图像，文本，编程源代码[45]，[122]和多智能体系统[63]，[66]，

[76]。由于长度限制，我们只会详细介绍前两种情况。 粗略地说，有两种方法将图神经网络应用于非结构场景：（1）结合来自其他领域的结构信息以改善性能，例如使用知识图中的信息来缓解图像中的零射击问题 任务; （2）推断或假设场景中的关系结构，然后应用模型来解决图上定义的问题，例如[48]中将文本建模为图形的方法。

3.2.1 Image

Image Classification Image classification is a very basic and important task in the field of computer vision, which attracts much attention and has many famous datasets like ImageNet [123]. Recent progress in image classifica-tion benefits from big data and the strong power of GPU computation, which allows us to train a classifier without extracting structural information from images. However, zero-shot and few-shot learning become more and more popular in the field of image classification, because most models can achieve similar performance with enough data. There are several works leveraging graph neural networks to incorporate structural information in image classification. First, knowledge graphs can be used as extra information to guide zero-short recognition classification [29], [94]. [94] builds a knowledge graph where each node corresponds to an object category and takes the word embeddings of nodes as input for predicting the classifier of different categories. As over-smoothing effect happens with the deep depth of convolution architecture, the 6-layer GCN used in [94] would wash out much useful information in the representa-tion. To solve the smoothing problem in the propagation of GCN, [29] managed to use single layer GCN with a larger neighborhood which includes both one-hop and multi-hops nodes in the graph. And it proved effective in building a zero-shot classifier with existing ones.

Except for the knowledge graph, the similarity between images in the dataset is also helpful for the few-shot learning

[93].[93] proposed to build a weighted full-connected image network based on the similarity and do message passing in the graph for few-shot recognition. As most knowledge graphs are large for reasoning, [96] selects some related entities to build a sub-graph based on the result of ob-ject detection and applies GGNN to the extracted graph for prediction. Besides, [95] proposed to construct a new knowledge graph where the entities are all the categories. And, they defined three types of label relations: super-subordinate, positive correlation, and negative correlation and propagate the confidence of labels in the graph directly.

Visual Reasoning Computer-vision systems usually need to perform reasoning by incorporating both spatial and
semantic information. So it is natural to generate graphs for reasoning tasks.

A typical visual reasoning task is visual question answer-ing(VQA), [97] respectively constructs image scene graph and question syntactic graph. Then it applies GGNN to train the embeddings for predicting the final answer. Despite spatial connections among objects, [124] builds the rela-tional graphs conditioned on the questions. With knowledge graphs, [92], [98] could perform finer relation exploration and more interpretable reasoning process.

Other applications of visual reasoning include object detection, interaction detection, and region classification. In object detection [99], [100], GNNs are used to calculate RoI features; In interaction detection [101], [102], GNNs are message passing tools between human and objects; In region classification [103], GNNs perform reasoning on graphs which connects regions and classes.

Semantic Segmentation Semantic segmentation is a cru-cial step toward image understanding. The task here is to assign a unique label (or category) to every single pixel in the image, which can be considered as a dense classification problem. However, regions in images are often not grid-like and need non-local information, which leads to the failure of traditional CNN. Several works utilized graph-structured data to handle it.

[49]proposed Graph-LSTM to model long-term de-pendency together with spatial connections by building graphs in form of distance-based superpixel map and ap-plying LSTM to propagate neighborhood information glob-ally. Subsequent work improved it from the perspective of encoding hierarchical information [104].

Furthermore, 3D semantic segmentation (RGBD seman-tic segmentation) and point clouds classification utilize more geometric information and therefore are hard to model by a 2D CNN. [107] constructs a K nearest neighbors (KNN) graph and uses a 3D GNN as propagation model. After unrolling for several steps, the prediction model takes the hidden state of each node as input and predict its semantic label.
图像分类图像分类是计算机视觉领域中一项非常基础和重要的任务，它引起了很多关注，并有许多着名的数据集，如ImageNet [123]。图像分类的最新进展受益于大数据和GPU计算的强大功能，这使我们能够在不从图像中提取结构信息的情况下训练分类器。然而，零射击和少射击学习在图像分类领域变得越来越流行，因为大多数模型可以用足够的数据实现类似的性能。有几种工作利用图形神经网络将结构信息结合到图像分类中。首先，知识图可以作为额外信息来指导零短识别分类[29]，[94]。 [94]构建知识图，其中每个节点对应于对象类别，并将节点的嵌入作为输入以预测不同类别的分类器。由于过度平滑效应发生在深度卷积结构中，[94]中使用的6层GCN将在表示中清除许多有用的信息。为了解决GCN传播中的平滑问题，[29]设法使用具有较大邻域的单层GCN，其中包括图中的单跳和多跳节点。事实证明，它可以有效地构建现有的零射击分类器。

除知识图外，数据集中图像之间的相似性也有助于少数学习

[93]。[93]提出建立一个基于相似度的加权全连通图像网络，并在图中进行消息传递以进行几次识别。由于大多数知识图对于推理都很大，[96]选择一些相关实体来构建基于对象检测结果的子图，并将GGNN应用于提取的图以进行预测。此外，[95]提出构建一个新的知识图，其中实体是所有类别。并且，他们定义了三种类型的标签关系：超级下属，正相关和负相关，并直接传播图中标签的置信度。

视觉推理计算机视觉系统通常需要通过结合空间和空间来进行推理
语义信息。因此，为推理任务生成图表是很自然的。

典型的视觉推理任务是视觉问题回答（VQA），[97]分别构建图像场景图和问题句法图。然后它应用GGNN来训练嵌入以预测最终答案。尽管对象之间存在空间联系，[124]建立了以问题为条件的相关图。利用知识图，[92]，[98]可以进行更精细的关系探索和更可解释的推理过程。

视觉推理的其他应用包括对象检测，交互检测和区域分类。在对象检测[99]，[100]中，GNN用于计算RoI特征;在交互检测[101]，[102]中，GNN是人与物之间的消息传递工具;在区域分类[103]中，GNN在连接区域和类的图上进行推理。

语义分割语义分割是图像理解的关键步骤。这里的任务是为图像中的每个像素分配唯一的标签（或类别），这可以被视为密集的分类问题。然而，图像中的区域通常不是网格状的并且需要非本地信息，这导致传统CNN的失败。一些作品利用图形结构数据来处理它。

[49]提出Graph-LSTM通过以基于距离的超像素图形式构建图形并应用LSTM来全局传播邻域信息，从而模拟长期依赖性和空间连接。后续工作从编码分层信息的角度对其进行了改进[104]。

此外，3D语义分割（RGBD语义分割）和点云分类利用更多的几何信息，因此难以通过2D CNN进行建模。 [107]构造K个最近邻（KNN）图并使用3D GNN作为传播模型。在展开几个步骤之后，预测模型将每个节点的隐藏状态作为输入并预测其语义标签。

As there are always too many points, [105] solved large-scale 3D point clouds segmentation by building superpoint graphs and generating embeddings for them. To classify supernodes, [105] leverages GGNN and graph convolution.

[106]proposed to model point interactions through edges. They calculate edge representation vectors by feeding the coordinates of its terminal nodes. Then node embed-dings are updated by edge aggregation.
由于总是有太多的点，[105]通过构建超点图并为它们生成嵌入来解决大规模3D点云分割。 为了对超节点进行分类，[105]利用GGNN和图卷积。

[106]建议通过边缘模拟点相互作用。 它们通过馈送其终端节点的坐标来计算边缘表示向量。 然后通过边缘聚合更新节点嵌入。

3.2.2 Text

The graph neural networks could be applied to several tasks based on texts. It could be applied to both sentence-level tasks(e.g. text classification) as well as word-level tasks(e.g. sequence labeling). We will introduce several major applica-tions on text in the following.

Text classification Text classification is an important and classical problem in natural language processing. The classi-cal GCN models [1], [2], [20], [21], [36], [38] and GAT model [54]are applied to solve the problem, but they only use the structural information between the documents and they don’t use much text information. [79] proposed a graph-CNN based deep learning model to first convert texts to graph-of-words, and then use graph convolution operations in [40] to convolve the word graph. [48] proposed the Sentence LSTM to encode text. It views the whole sentence as a single state, which consists of sub-states for individual words and an overall sentence-level state. It uses the global sentence-level representation for classification tasks. These methods either view a document or a sentence as a graph of word nodes or rely on the document citation relation to con-struct the graph. [80] regards the documents and words as nodes to construct the corpus graph (hence heterogeneous graph) and uses the Text GCN to learning embeddings of words and documents. Sentiment classification could also be regarded as a text classification problem and a Tree-LSTM approach is proposed by [46].

Sequence labeling As each node in GNNs has its hidden state, we can utilize the hidden state to address the sequence labeling problem if we consider every word in the sentence as a node. [48] utilizes the Sentence LSTM to label the sequence. It has conducted experiments on POS-tagging and NER tasks and achieves state-of-the-art performance.

Semantic role labeling is another task of sequence label-ing. [81] proposed a Syntactic GCN to solve the problem. The Syntactic GCN which operates on the direct graph with labeled edges is a special variant of the GCN [2]. It integrates edge-wise gates which let the model regulate contributions of individual dependency edges. The Syntactic GCNs over syntactic dependency trees are used as sentence encoders to learn latent feature representations of words in the sentence.

[81]also reveals that GCNs and LSTMs are functionally complementary in the task.

Neural machine translation The neural machine trans-lation task is usually considered as a sequence-to-sequence task. [52] introduces the attention mechanisms and replaces the most commonly used recurrent or convolutional layers. In fact, the Transformer assumes a fully connected graph structure between linguistic entities.

One popular application of GNN is to incorporate the syntactic or semantic information into the NMT task. [82] utilizes the Syntactic GCN on syntax-aware NMT tasks.
图神经网络可以应用于基于文本的若干任务。它可以应用于句子级任务（例如文本分类）以及单词级任务（例如序列标记）。我们将在下文中介绍几个主要的文本应用程序。

文本分类文本分类是自然语言处理中的一个重要且经典的问题。分类GCN模型[1]，[2]，[20]，[21]，[36]，[38]和GAT模型[54]用于解决问题，但它们只使用之间的结构信息这些文件并没有使用太多的文字信息。 [79]提出了一种基于图CNN的深度学习模型，首先将文本转换为单词图形，然后在[40]中使用图卷积运算来卷积单词图。 [48]提出了句子LSTM来编码文本。它将整个句子视为单个状态，其由单个词的子状态和整个句子级状态组成。它使用全局句子级别表示来进行分类任务。这些方法或者将文档或句子视为单词节点的图形，或者依赖于文档引用关系来构造图形。 [80]将文档和单词视为节点来构建语料库图（因此是异构图），并使用Text GCN来学习单词和文档的嵌入。情感分类也可以被视为文本分类问题，并且[46]提出了Tree-LSTM方法。

序列标记由于GNN中的每个节点都有隐藏状态，如果我们将句子中的每个单词都视为一个节点，我们就可以利用隐藏状态来解决序列标记问题。 [48]利用Sentence LSTM来标记序列。它已经对POS标签和NER任务进行了实验，并实现了最先进的性能。

语义角色标记是序列标记的另一个任务。 [81]提出了一个Syntactic GCN来解决这个问题。在具有标记边的直接图上操作的语法GCN是GCN的特殊变体[2]。它集成了边缘门，使模型可以调节各个依赖边缘的贡献。句法依赖树上的句法GCN用作句子编码器，以学习句子中单词的潜在特征表示。

[81]还揭示了GCN和LSTM在任务中的功能互补。

神经机器翻译神经机器翻译任务通常被视为序列到序列任务。 [52]介绍了注意机制并取代了最常用的复发或卷积层。实际上，Transformer假设语言实体之间存在完全连接的图形结构。

GNN的一个流行应用是将语法或语义信息合并到NMT任务中。 [82]在语法感知NMT任务上使用Syntactic GCN。
[83]incorporates information about the predicate-argument structure of source sentences (namely, semantic-role repre-sentations) using Syntactic GCN and compares the results of incorporating only syntactic or semantic information or both of the information into the task. [31] utilizes the GGNN in syntax-aware NMT. It converts the syntactic dependency graph into a new structure called the Levi graph by turning the edges into additional nodes and thus edge labels can be represented as embeddings.

Relation extraction Extracting semantic relations be-tween entities in texts is an important and well-studied task. Some systems treat this task as a pipeline of two separated tasks, named entity recognition and relation extraction. [84] proposed an end-to-end relation extraction model by using bidirectional sequential and tree-structured LSTM-RNNs. [86] proposed an extension of graph convolutional networks
[83]使用Syntactic GCN结合有关源语句的谓词 - 参数结构的信息（即语义 - 角色表示），并比较仅将句法或语义信息或两者信息合并到任务中的结果。 [31]在语法感知NMT中使用GGNN。 它通过将边缘转换为附加节点将语法依赖图转换为称为Levi图的新结构，因此边标签可以表示为嵌入。

关系提取提取文本中实体之间的语义关系是一项重要且经过充分研究的任务。 有些系统将此任务视为两个独立任务的管道，称为实体识别和关系提取。 [84]通过使用双向顺序和树形结构的LSTM-RNN提出了端到端关系提取模型。 [86]提出了图卷积网络的扩展

16

that is tailored for relation extraction and applied a pruning strategy to the input trees.

Cross-sentence N-ary relation extraction detects relations among n entities across multiple sentences. [34] explores a general framework for cross-sentence n-ary relation extrac-tion based on graph LSTMs. It splits the input graph into two DAGs while important information could be lost in the splitting procedure. [85] proposed a graph-state LSTM model. It keeps the original graph structure and speeds up computation by allowing more parallelization.

Event extraction Event extraction is an important in-formation extraction task to recognize instances of speci-fied types of events in texts. [87] investigates a convolu-tional neural network (which is the Syntactic GCN exactly) based on dependency trees to perform event detection.

[88]proposed a Jointly Multiple Events Extraction (JMEE) framework to jointly extract multiple event triggers and arguments by introducing syntactic shortcut arcs to enhance information flow to attention-based graph convolution net-works to model graph information.

Other applications GNNs could also be applied to many other applications. There are several works focus on the AMR to text generation task. A Sentence-LSTM based method [89] and a GGNN based method [31] have been proposed in this area. [46] uses the Tree LSTM to model the semantic relatedness of two sentences. And [90] exploits the Sentence LSTM to solve the multi-hop reading compre-hension problem. Another important direction is relational reasoning, relational networks [69], interaction networks [4] and recurrent relational networks [91] are proposed to solve the relational reasoning task based on text. The works cited above are not an exhaustive list, and we encourage our readers to find more works and application domains of graph neural networks that they are interested in.
这是为关系提取量身定制的，并将修剪策略应用于输入树。

跨句子N元关系提取检测多个句子中n个实体之间的关系。 [34]探讨了基于图LSTM的跨句子n元关系提取的一般框架。它将输入图分成两个DAG，而重要信息可能在分割过程中丢失。 [85]提出了图形状态LSTM模型。它保留了原始图形结构，并通过允许更多并行化来加速计算。

事件提取事件提取是一项重要的信息提取任务，用于识别文本中特定类型事件的实例。 [87]基于依赖树来研究卷积神经网络（精确地说是语法GCN）以执行事件检测。

[88]提出了一个联合多事件提取（JMEE）框架，通过引入句法快捷方式弧来共同提取多个事件触发器和参数，以增强基于注意力的图卷积网络的信息流，以模拟图形信息。

其他应用程序GNN也可以应用于许多其他应用程序。有几项工作侧重于AMR到文本生成任务。在该领域已经提出了基于句子-LSTM的方法[89]和基于GGNN的方法[31]。 [46]使用树LSTM来模拟两个句子的语义相关性。 [90]利用Sentence LSTM来解决多跳阅读压缩问题。另一个重要方向是关系推理，关系网络[69]，交互网络[4]和循环关系网络[91]被提出来解决基于文本的关系推理任务。上面引用的作品并不是一个详尽的列表，我们鼓励读者找到他们感兴趣的图神经网络的更多作品和应用领域。

3.3 Other Scenarios

Besides structural and non-structural scenarios, there are some other scenarios where graph neural networks play an important role. In this subsection, we will introduce generative graph models and combinatorial optimization with GNNs.
除了结构和非结构场景之外，还有一些其他场景，其中图神经网络起着重要作用。 在本小节中，我们将介绍生成图模型和GNN组合优化。

3.3.1 Generative Models

Generative models for real-world graphs has drawn signifi-cant attention for its important applications including mod-eling social interactions, discovering new chemical struc-tures, and constructing knowledge graphs. As deep learning methods have powerful ability to learn the implicit distribu-tion of graphs, there is a surge in neural graph generative models recently.

NetGAN [114] is one of the first work to build neural graph generative model, which generates graphs via ran-dom walks. It transformed the problem of graph generation to the problem of walk generation which takes the random walks from a specific graph as input and trains a walk generative model using GAN architecture. While the gen-erated graph preserves important topological properties of

the original graph, the number of nodes is unable to change in the generating process, which is as same as the original graph. GraphRNN [125] managed to generate the adjacency matrix of a graph by generating the adjacency vector of each node step by step, which can output required networks having different numbers of nodes.

Instead of generating adjacency matrix sequentially, MolGAN [117] predicts discrete graph structure (the adja-cency matrix) at once and utilizes a permutation-invariant discriminator to solve the node variant problem in the adjacency matrix. Besides, it applies a reward network for RL-based optimization towards desired chemical proper-ties. What’s more, [115] proposed constrained variational autoencoders to ensure the semantic validity of generated graphs. And, GCPN [116] incorporated domain-specific rules through reinforcement learning.

[126]proposed a model which generates edges and nodes sequentially and utilizes a graph neural network to extract the hidden state of the current graph which is used to decide the action in the next step during the sequential generative process.
现实世界图的生成模型已经引起了人们对其重要应用的重视，包括模拟社会交互，发现新的化学结构，以及构建知识图。由于深度学习方法具有强大的学习图的隐式分布的能力，最近神经图生成模型出现了激增。

NetGAN [114]是第一个构建神经图生成模型的工作之一，该模型通过随机漫游生成图形。它将图形生成的问题转化为步行生成问题，该问题将来自特定图形的随机游走作为输入，并使用GAN架构训练步行生成模型。虽然生成的图保留了重要的拓扑性质

在原始图中，节点的数量在生成过程中无法改变，这与原始图相同。 GraphRNN [125]设法通过逐步生成每个节点的邻接向量来生成图的邻接矩阵，其可以输出具有不同节点数的所需网络。

MolGAN [117]不是依次生成邻接矩阵，而是立刻预测离散图结构（邻接矩阵），并利用置换不变判别器来解决邻接矩阵中的节点变异问题。此外，它还将基于RL的优化奖励网络应用于所需的化学特性。更重要的是，[115]提出了约束变分自动编码器来确保生成的图形的语义有效性。并且，GCPN [116]通过强化学习纳入了特定领域的规则。

[126]提出了一种模型，该模型顺序地生成边缘和节点，并利用图形神经网络来提取当前图形的隐藏状态，该状态用于在顺序生成过程期间决定下一步骤中的动作。

3.3.2 Combinatorial Optimization

Combinatorial optimization problems over graphs are set of NP-hard problems which attract much attention from scientists of all fields. Some specific problems like travel-ing salesman problem (TSP) and minimum spanning trees (MST) have got various heuristic solutions. Recently, using a deep neural network for solving such problems has been a hotspot, and some of the solutions further leverage graph neural network because of their graph structure.

[127]first proposed a deep-learning approach to tackle TSP. Their method consists of two parts: a Pointer Net-work [128] for parameterizing rewards and a policy gradi-ent [129] module for training. This work has been proved to be comparable with traditional approaches. However, Pointer Networks are designed for sequential data like texts, while order-invariant encoders are more appropriate for such work.

[130]improved the approach by including graph neural networks. They first obtain the node embeddings from structure2vec [67], which is a variant of GCN, then feed them into a Q-learning module for making decisions. This work achieved better performance than previous algo-rithms, which proved the representation power of graph neural networks.

[113]proposed an attention-based encoder-decoder al-gorithm. Such a method can be regarded as a graph at-tention network whose readout phase is an attention-based decoder instead of a reinforcement learning module, which is theoretically efficient for training.

[111]focused on Quadratic Assignment Problem i.e. measuring the similarity of two graphs. The GNN based model learns node embeddings for each graph indepen-dently and matches them using attention mechanism. This method offers intriguingly good performance even in regimes where standard relaxation-based techniques appear to suffer.

图中的组合优化问题是NP难问题的集合，引起了各个领域科学家的广泛关注。旅行商问题（TSP）和最小生成树（MST）等一些具体问题得到了各种启发式解决方案。最近，使用深度神经网络来解决这些问题已成为热点，并且由于其图形结构，一些解决方案进一步利用图形神经网络。

[127]首先提出了一种解决TSP的深度学习方法。他们的方法由两部分组成：用于参数化奖励的指针网络[128]和用于训练的策略梯度模块[129]。事实证明，这项工作可与传统方法相媲美。但是，指针网络设计用于文本等顺序数据，而顺序不变编码器更适合此类工作。

[130]通过包括图神经网络改进了方法。他们首先从structure2vec [67]获取节点嵌入，这是GCN的变体，然后将它们提供给Q学习模块以进行决策。这项工作比先前的算法实现了更好的性能，证明了图神经网络的表示能力。

[113]提出了一种基于注意力的编码器 - 解码器算法。这种方法可以被视为图形注意网络，其读出阶段是基于注意力的解码器而不是强化学习模块，这在理论上对于训练是有效的。

[111]专注于二次分配问题，即测量两个图的相似性。基于GNN的模型独立地学习每个图的节点嵌入，并使用注意机制匹配它们。即使在基于标准松弛的技术似乎受到影响的制度中，该方法也提供了令人惊讶的良好性能。
17

[112]uses GNNs directly as classifiers who can perform dense prediction over a graph with pairwise edges. The rest of the model help GNNs do diverse choices and train efficiently.

[112]直接使用GNN作为分类器，可以对具有成对边的图进行密集预测。 模型的其余部分帮助GNN做出各种选择并有效地进行训练。

4 OPEN PROBLEMS

Although GNNs have achieved great success in different fields, it is remarkable that GNN models are not good enough to offer satisfying solutions for any graph in any condition. In this section, we will state some open problems for further researches.

Shallow Structure Traditional deep neural networks can stack hundreds of layers to get better performance, because deeper structure has more parameters, which improve the expressive power significantly. However, graph neural net-works are always shallow, most of which are no more than three layers. As experiments in [62] show, stacking multiple GCN layers will result in over-smoothing, that is to say, all vertices will converge to the same value. Although some researchers have managed to tackle this problem [45], [62], it remains to be the biggest limitation of GNN. Designing real deep GNN is an exciting challenge for future research, and will be a considerable contribution to the understanding of GNN.

Dynamic Graphs Another challenging problem is how to deal with graphs with dynamic structures. Static graphs are stable so they can be modeled feasibly, while dynamic graphs introduce changing structures. When edges and nodes appear or disappear, GNN can not change adaptively. Dynamic GNN is being actively researched on and we believe it to be a big milestone about the stability and adaptability of general GNN.

Non-Structural Scenarios Although we have discussed the applications of GNN on non-structural scenarios, we found that there is no optimal methods to generate graphs from raw data. In image domain, some work utilizes CNN to obtain feature maps then upsamples them to form su-perpixels as nodes [49], while other ones directly leverage some object detection algorithms to get object nodes. In text domain [103], some work employs syntactic trees as syntactic graphs while others adopt fully connected graphs. Therefore, finding the best graph generation approach will offer a wider range of fields where GNN could make contri-bution.

Scalability How to apply embedding methods in web-scale conditions like social networks or recommendation systems has been a fatal problem for almost all graph em-bedding algorithms, and GNN is not an exception. Scaling up GNN is difficult because many of the core steps are computational consuming in big data environment. There are several examples about this phenomenon: First, graph data are not regular Euclidean, each node has its own neighborhood structure so batches can not be applied. Then, calculating graph Laplacian is also unfeasible when there are millions of nodes and edges. Moreover, we need to point out that scaling determines whether an algorithm is able to be applied into practical use. Several work has proposed

their solutions to this problem [120] and we are paying close attention to the progress.

尽管GNN在不同领域取得了巨大成功，但值得注意的是，GNN模型不足以在任何条件下为任何图形提供令人满意的解决方案。在本节中，我们将陈述一些开放性问题以供进一步研究。

浅层结构传统的深度神经网络可以叠加数百层以获得更好的性能，因为更深的结构具有更多的参数，从而显着提高了表达能力。然而，图神经网络总是很浅，大多数不超过三层。正如[62]中的实验所示，堆叠多个GCN层将导致过度平滑，也就是说，所有顶点将收敛到相同的值。尽管一些研究人员设法解决了这个问题[45]，[62]，但它仍然是GNN的最大限制。设计真正的深度GNN对于未来的研究来说是一个令人兴奋的挑战，并将对理解GNN做出相当大的贡献。

动态图形另一个具有挑战性的问题是如何处理具有动态结构的图形。静态图是稳定的，因此可以可行地建模，而动态图则引入变化的结构。当边和节点出现或消失时，GNN无法自适应地更改。动态GNN正在积极研究中，我们认为它是一般GNN的稳定性和适应性的重要里程碑。

非结构场景尽管我们已经讨论了GNN在非结构场景中的应用，但我们发现没有从原始数据生成图的最佳方法。在图像域中，一些工作利用CNN获取特征映射，然后对它们进行上采样以形成su-perpixels作为节点[49]，而其他工作则直接利用一些对象检测算法来获取对象节点。在文本域[103]中，一些工作使用句法树作为句法图，而其他工作采用完全连通的图。因此，找到最佳图形生成方法将提供更广泛的领域，GNN可以做出贡献。

可扩展性如何在社交网络或推荐系统等网络规模条件下应用嵌入方法对于几乎所有的图形嵌入算法都是一个致命的问题，而GNN也不例外。扩展GNN很困难，因为许多核心步骤在大数据环境中都是计算消耗。关于这种现象有几个例子：首先，图形数据不是规则的欧几里德，每个节点都有自己的邻域结构，因此不能应用批量。然后，当存在数百万个节点和边缘时，计算图拉普拉斯算子也是不可行的。此外，我们需要指出缩放确定算法是否能够应用于实际应用。有几项工作已提出

他们解决这个问题[120]，我们正在密切关注这一进展。

5 CONCLUSION

Over the past few years, graph neural networks have be-come powerful and practical tools for machine learning tasks in graph domain. This progress owes to advances in expressive power, model flexibility, and training algorithms. In this survey, we conduct a comprehensive review of graph neural networks. For GNN models, we introduce its variants categorized by graph types, propagation types, and training types. Moreover, we also summarize several general frame-works to uniformly represent different variants. In terms of application taxonomy, we divide the GNN applications into structural scenarios, non-structural scenarios, and other scenarios, then give a detailed review for applications in each scenario. Finally, we suggest four open problems indi-cating the major challenges and future research directions of graph neural networks, including model depth, scalability, the ability to deal with dynamic graphs and non-structural scenarios.
在过去的几年中，图形神经网络已成为图域中机器学习任务的强大而实用的工具。 这一进展归功于表现力，模型灵活性和训练算法的进步。 在本次调查中，我们对图神经网络进行了全面审查。 对于GNN模型，我们引入了按图类型，传播类型和训练类型分类的变体。 此外，我们还总结了几个通用框架，以统一表示不同的变体。 在应用程序分类方面，我们将GNN应用程序划分为结构场景，非结构场景和其他场景，然后对每个场景中的应用程序进行详细审查。 最后，我们提出了四个开放性问题，指出了图神经网络的主要挑战和未来研究方向，包括模型深度，可扩展性，处理动态图和非结构场景的能力。

REFERENCES

[1]W. L. Hamilton, Z. Ying, and J. Leskovec, “Inductive representa-tion learning on large graphs,” NIPS 2017, pp. 1024–1034, 2017.

[2]T. N. Kipf and M. Welling, “Semi-supervised classification with graph convolutional networks,” ICLR 2017, 2017.
[3]A. Sanchez-Gonzalez, N. Heess, J. T. Springenberg, J. Merel, M. Riedmiller, R. Hadsell, and P. Battaglia, “Graph networks as learnable physics engines for inference and control,” arXiv preprint arXiv:1806.01242, 2018.

[4]P. Battaglia, R. Pascanu, M. Lai, D. J. Rezende et al., “Interaction networks for learning about objects, relations and physics,” in NIPS 2016, 2016, pp. 4502–4510.
[5]A. Fout, J. Byrd, B. Shariat, and A. Ben-Hur, “Protein interface prediction using graph convolutional networks,” in NIPS 2017, 2017, pp. 6530–6539.
[6]T. Hamaguchi, H. Oiwa, M. Shimbo, and Y. Matsumoto, “Knowl-edge transfer for out-of-knowledge-base entities : A graph neural network approach,” in IJCAI 2017, 2017, pp. 1802–1808.

[7]H. Dai, E. B. Khalil, Y. Zhang, B. Dilkina, and L. Song, “Learn-ing combinatorial optimization algorithms over graphs,” arXiv preprint arXiv:1704.01665, 2017.
[8]Y. LeCun, L. Bottou, Y. Bengio, and P. Haffner, “Gradient-based learning applied to document recognition,” Proceedings of the IEEE, vol. 86, no. 11, pp. 2278–2324, 1998.
[9]Y. LeCun, Y. Bengio, and G. Hinton, “Deep learning,” Nature 2015, vol. 521, no. 7553, p. 436, 2015.
[10]F. R. Chung and F. C. Graham, Spectral graph theory. American Mathematical Soc., 1997, no. 92.
[11]T. Mikolov, K. Chen, G. Corrado, and J. Dean, “Efficient esti-mation of word representations in vector space,” arXiv preprint arXiv:1301.3781, 2013.

[12]B. Perozzi, R. Al-Rfou, and S. Skiena, “Deepwalk: Online learning of social representations,” in SIGKDD 2014. ACM, 2014, pp. 701– 710.
[13]A. Grover and J. Leskovec, “node2vec: Scalable feature learning for networks,” in SIGKDD. ACM, 2016, pp. 855–864.

[14]J. Tang, M. Qu, M. Wang, M. Zhang, J. Yan, and Q. Mei, “Line: Large-scale information network embedding,” in WWW 2015, 2015, pp. 1067–1077.
[15]C. Yang, Z. Liu, D. Zhao, M. Sun, and E. Y. Chang, “Network representation learning with rich text information.” in IJCAI 2015, 2015, pp. 2111–2117.
[16]W. L. Hamilton, R. Ying, and J. Leskovec, “Representation learning on graphs: Methods and applications,” arXiv preprint arXiv:1709.05584, 2017.

18

[17]T. Kawamoto, M. Tsubaki, and T. Obuchi, “Mean-field theory of graph neural networks in graph partitioning,” in NeurIPS 2018, 2018, pp. 4366–4376.
[18]F. Scarselli, M. Gori, A. C. Tsoi, M. Hagenbuchner, and G. Monfar-dini, “The graph neural network model,” IEEE TNN 2009, vol. 20, no. 1, pp. 61–80, 2009.

[19]——, “Computational capabilities of graph neural networks,” IEEE TNN 2009, vol. 20, no. 1, pp. 81–102, 2009.
[20]F. Monti, D. Boscaini, J. Masci, E. Rodola, J. Svoboda, and M. M. Bronstein, “Geometric deep learning on graphs and manifolds using mixture model cnns,” CVPR 2017, pp. 5425–5434, 2017.

[21]J. Atwood and D. Towsley, “Diffusion-convolutional neural net-works,” in NIPS 2016, 2016, pp. 1993–2001.
[22]J. Masci, D. Boscaini, M. Bronstein, and P. Vandergheynst, “Geodesic convolutional neural networks on riemannian mani-folds,” in ICCV workshops 2015, 2015, pp. 37–45.

[23]D. Boscaini, J. Masci, E. Rodola,` and M. Bronstein, “Learning shape correspondence with anisotropic convolutional neural net-works,” in NIPS 2016, 2016, pp. 3189–3197.

[24]M. M. Bronstein, J. Bruna, Y. LeCun, A. Szlam, and P. Van-dergheynst, “Geometric deep learning: going beyond euclidean data,” IEEE SPM 2017, vol. 34, no. 4, pp. 18–42, 2017.

[25]J. Gilmer, S. S. Schoenholz, P. F. Riley, O. Vinyals, and G. E. Dahl, “Neural message passing for quantum chemistry,” arXiv preprint arXiv:1704.01212, 2017.

[26]X. Wang, R. Girshick, A. Gupta, and K. He, “Non-local neural networks,” arXiv preprint arXiv:1711.07971, vol. 10, 2017.
[27]P. W. Battaglia, J. B. Hamrick, V. Bapst, A. Sanchez-Gonzalez,

V.Zambaldi, M. Malinowski, A. Tacchetti, D. Raposo, A. Santoro,

R.Faulkner et al., “Relational inductive biases, deep learning, and graph networks,” arXiv preprint arXiv:1806.01261, 2018.
[28]M. A. Khamsi and W. A. Kirk, An introduction to metric spaces and fixed point theory. John Wiley & Sons, 2011, vol. 53.
[29]M. Kampffmeyer, Y. Chen, X. Liang, H. Wang, Y. Zhang, and E. P. Xing, “Rethinking knowledge graph propagation for zero-shot learning,” arXiv preprint arXiv:1805.11724, 2018.

[30]Y. Zhang, Y. Xiong, X. Kong, S. Li, J. Mi, and Y. Zhu, “Deep collective classification in heterogeneous information networks,” in WWW 2018, 2018, pp. 399–408.

[31]D. Beck, G. Haffari, and T. Cohn, “Graph-to-sequence learning using gated graph neural networks,” in ACL 2018, 2018, pp. 273– 283.

[32]M. Schlichtkrull, T. N. Kipf, P. Bloem, R. van den Berg, I. Titov, and M. Welling, “Modeling relational data with graph convolu-tional networks,” in ESWC 2018. Springer, 2018, pp. 593–607.
[33]D. K. Duvenaud, D. Maclaurin, J. Aguileraiparraguirre,

R.Gomezbombarelli, T. D. Hirzel, A. Aspuruguzik, and R. P. Adams, “Convolutional networks on graphs for learning molec-ular fingerprints,” NIPS 2015, pp. 2224–2232, 2015.

[34]N. Peng, H. Poon, C. Quirk, K. Toutanova, and W.-t. Yih, “Cross-sentence n-ary relation extraction with graph lstms,” arXiv preprint arXiv:1708.03743, 2017.

[35]J. Bruna, W. Zaremba, A. Szlam, and Y. Lecun, “Spectral networks and locally connected networks on graphs,” ICLR 2014, 2014.

[36]M. Henaff, J. Bruna, and Y. Lecun, “Deep convolutional networks on graph-structured data.” arXiv: Learning, 2015.
[37]D. K. Hammond, P. Vandergheynst, and R. Gribonval, “Wavelets on graphs via spectral graph theory,” Applied and Computational Harmonic Analysis, vol. 30, no. 2, pp. 129–150, 2011.

[38]M. Defferrard, X. Bresson, and P. Vandergheynst, “Convolutional neural networks on graphs with fast localized spectral filtering,” NIPS 2016, pp. 3844–3852, 2016.

[39]Y. C. Ng, N. Colombo, and R. Silva, “Bayesian semi-supervised learning with graph gaussian processes,” in NeurIPS 2018, 2018, pp. 1690–1701.

[40]M. Niepert, M. Ahmed, and K. Kutzkov, “Learning convolutional neural networks for graphs,” in ICML 2016, 2016, pp. 2014–2023.
[41]K. He, X. Zhang, S. Ren, and J. Sun, “Identity mappings in deep residual networks,” in ECCV 2016. Springer, 2016, pp. 630–645.
[42]J. Chang, J. Gu, L. Wang, G. Meng, S. Xiang, and C. Pan, “Structure-aware convolutional neural networks,” in NeurIPS 2018, 2018, pp. 11–20.

[43]K. Cho, B. Van Merrienboer, C. Gulcehre, D. Bahdanau,

F.Bougares, H. Schwenk, and Y. Bengio, “Learning phrase rep-resentations using rnn encoder–decoder for statistical machine translation,” EMNLP 2014, pp. 1724–1734, 2014.

[44]S. Hochreiter and J. Schmidhuber, “Long short-term memory,” Neural Computation, vol. 9, no. 8, pp. 1735–1780, 1997.

[45]Y. Li, D. Tarlow, M. Brockschmidt, and R. S. Zemel, “Gated graph sequence neural networks,” arXiv: Learning, 2016.

[46]K. S. Tai, R. Socher, and C. D. Manning, “Improved semantic representations from tree-structured long short-term memory networks,” IJCNLP 2015, pp. 1556–1566, 2015.
[47]V. Zayats and M. Ostendorf, “Conversation modeling on reddit using a graph-structured lstm,” TACL 2018, vol. 6, pp. 121–132, 2018.

[48]Y. Zhang, Q. Liu, and L. Song, “Sentence-state lstm for text representation,” ACL 2018, vol. 1, pp. 317–327, 2018.
[49]X. Liang, X. Shen, J. Feng, L. Lin, and S. Yan, “Semantic object parsing with graph lstm,” ECCV 2016, pp. 125–143, 2016.

[50]D. Bahdanau, K. Cho, and Y. Bengio, “Neural machine translation by jointly learning to align and translate,” ICLR 2015, 2015.
[51]J. Gehring, M. Auli, D. Grangier, and Y. N. Dauphin, “A convolu-tional encoder model for neural machine translation,” ACL 2017, vol. 1, pp. 123–135, 2017.

[52]A. Vaswani, N. Shazeer, N. Parmar, L. Jones, J. Uszkoreit, A. N. Gomez, and L. Kaiser, “Attention is all you need,” NIPS 2017, pp. 5998–6008, 2017.
[53]J. Cheng, L. Dong, and M. Lapata, “Long short-term memory-networks for machine reading,” EMNLP 2016, pp. 551–561, 2016.
[54]P. Velickovic, G. Cucurull, A. Casanova, A. Romero, P. Lio, and
Y.Bengio, “Graph attention networks,” ICLR 2018, 2018.
[55]K. He, X. Zhang, S. Ren, and J. Sun, “Deep residual learning for image recognition,” CVPR 2016, pp. 770–778, 2016.

[56]A. Rahimi, T. Cohn, and T. Baldwin, “Semi-supervised user geolocation via graph convolutional networks,” ACL 2018, vol. 1, pp. 2009–2019, 2018.

[57]J. G. Zilly, R. K. Srivastava, J. Koutnik, and J. Schmidhuber, “Recurrent highway networks.” ICML 2016, pp. 4189–4198, 2016.
[58]K. Xu, C. Li, Y. Tian, T. Sonobe, K. Kawarabayashi, and S. Jegelka, “Representation learning on graphs with jumping knowledge networks,” ICML 2018, pp. 5449–5458, 2018.
[59]J. Chen, T. Ma, and C. Xiao, “Fastgcn: fast learning with graph convolutional networks via importance sampling,” arXiv preprint arXiv:1801.10247, 2018.
[60]W. Huang, T. Zhang, Y. Rong, and J. Huang, “Adaptive sampling towards fast graph representation learning,” in NeurIPS 2018, 2018, pp. 4563–4572.

[61]J. Chen, J. Zhu, and L. Song, “Stochastic training of graph convolutional networks with variance reduction.” in ICML 2018, 2018, pp. 941–949.
[62]Q. Li, Z. Han, and X.-M. Wu, “Deeper insights into graph con-volutional networks for semi-supervised learning,” arXiv preprint arXiv:1801.07606, 2018.
[63]Y. Hoshen, “Vain: Attentional multi-agent predictive modeling,” in NIPS 2017, 2017, pp. 2701–2711.

[64]N. Watters, D. Zoran, T. Weber, P. Battaglia, R. Pascanu, and
A.Tacchetti, “Visual interaction networks: Learning a physics simulator from video,” in NIPS 2017, 2017, pp. 4539–4547.
[65]M. B. Chang, T. Ullman, A. Torralba, and J. B. Tenenbaum, “A compositional object-based approach to learning physical dynamics,” arXiv preprint arXiv:1612.00341, 2016.
[66]S. Sukhbaatar, R. Fergus et al., “Learning multiagent communica-tion with backpropagation,” in NIPS 2016, 2016, pp. 2244–2252.
[67]H. Dai, B. Dai, and L. Song, “Discriminative embeddings of latent variable models for structured data,” in ICML 2016, 2016, pp. 2702–2711.

[68]D. Raposo, A. Santoro, D. Barrett, R. Pascanu, T. Lillicrap, and

P.Battaglia, “Discovering objects and their relations from entan-gled scene representations,” arXiv preprint arXiv:1702.05068, 2017.
[69]A. Santoro, D. Raposo, D. G. Barrett, M. Malinowski, R. Pascanu,

P.Battaglia, and T. Lillicrap, “A simple neural network module for relational reasoning,” in NIPS 2017, 2017, pp. 4967–4976.
[70]M. Zaheer, S. Kottur, S. Ravanbakhsh, B. Poczos, R. R. Salakhut-dinov, and A. J. Smola, “Deep sets,” in NIPS 2017, 2017, pp. 3391– 3401.

[71]C. R. Qi, H. Su, K. Mo, and L. J. Guibas, “Pointnet: Deep learning on point sets for 3d classification and segmentation,” CVPR 2017, vol. 1, no. 2, p. 4, 2017.
[72]S. Kearnes, K. McCloskey, M. Berndl, V. Pande, and P. Riley, “Molecular graph convolutions: moving beyond fingerprints,” Journal of computer-aided molecular design, vol. 30, no. 8, pp. 595– 608, 2016.

19

[73]K. T. Schutt,¨ F. Arbabzadah, S. Chmiela, K. R. Muller,¨ and

A.Tkatchenko, “Quantum-chemical insights from deep tensor neural networks,” Nature communications, vol. 8, p. 13890, 2017.
[74]A. Buades, B. Coll, and J.-M. Morel, “A non-local algorithm for image denoising,” in CVPR 2005, vol. 2. IEEE, 2005, pp. 60–65.
[75]C. Tomasi and R. Manduchi, “Bilateral filtering for gray and color images,” in Computer Vision 1998. IEEE, 1998, pp. 839–846.
[76]T. Kipf, E. Fetaya, K.-C. Wang, M. Welling, and R. Zemel, “Neu-ral relational inference for interacting systems,” arXiv preprint arXiv:1802.04687, 2018.

[77]J. B. Hamrick, K. R. Allen, V. Bapst, T. Zhu, K. R. McKee, J. B. Tenenbaum, and P. W. Battaglia, “Relational inductive bias for physical construction in humans and machines,” arXiv preprint arXiv:1806.01203, 2018.
[78]T. Wang, R. Liao, J. Ba, and S. Fidler, “Nervenet: Learning structured policy with graph neural networks,” 2018.

[79]H. Peng, J. Li, Y. He, Y. Liu, M. Bao, L. Wang, Y. Song, and

Q.Yang, “Large-scale hierarchical text classification with recur-sively regularized deep graph-cnn,” in WWW 2018, 2018, pp. 1063–1072.

[80]L. Yao, C. Mao, and Y. Luo, “Graph convolutional networks for text classification,” arXiv preprint arXiv:1809.05679, 2018.
[81]D. Marcheggiani and I. Titov, “Encoding sentences with graph convolutional networks for semantic role labeling,” in EMNLP 2017, September 2017, pp. 1506–1515.

[82]J. Bastings, I. Titov, W. Aziz, D. Marcheggiani, and K. Simaan, “Graph convolutional encoders for syntax-aware neural machine translation,” EMNLP 2017, pp. 1957–1967, 2017.

[83]D. Marcheggiani, J. Bastings, and I. Titov, “Exploiting semantics in neural machine translation with graph convolutional net-works,” arXiv preprint arXiv:1804.08313, 2018.

[84]M. Miwa and M. Bansal, “End-to-end relation extraction us-ing lstms on sequences and tree structures,” arXiv preprint arXiv:1601.00770, 2016.

[85]L. Song, Y. Zhang, Z. Wang, and D. Gildea, “N-ary relation ex-traction using graph state lstm,” arXiv preprint arXiv:1808.09101, 2018.

[86]Y. Zhang, P. Qi, and C. D. Manning, “Graph convolution over pruned dependency trees improves relation extraction,” arXiv preprint arXiv:1809.10185, 2018.
[87]T. H. Nguyen and R. Grishman, “Graph convolutional networks with argument-aware pooling for event detection,” 2018.

[88]X. Liu, Z. Luo, and H. Huang, “Jointly multiple events extrac-tion via attention-based graph information aggregation,” arXiv preprint arXiv:1809.09078, 2018.
[89]L. Song, Y. Zhang, Z. Wang, and D. Gildea, “A graph-to-sequence model for amr-to-text generation,” arXiv preprint arXiv:1805.02473, 2018.

[90]L. Song, Z. Wang, M. Yu, Y. Zhang, R. Florian, and D. Gildea, “Exploring graph-structured passage representation for multi-hop reading comprehension with graph neural networks,” arXiv preprint arXiv:1809.02040, 2018.
[91]R. B. Palm, U. Paquet, and O. Winther, “Recurrent relational networks,” NeurIPS 2018, 2018.
[92]Z. Wang, T. Chen, J. Ren, W. Yu, H. Cheng, and L. Lin, “Deep reasoning with knowledge graph for social relationship under-standing,” arXiv preprint arXiv:1807.00504, 2018.

[93]V. Garcia and J. Bruna, “Few-shot learning with graph neural networks,” arXiv preprint arXiv:1711.04043, 2017.
[94]X. Wang, Y. Ye, and A. Gupta, “Zero-shot recognition via seman-tic embeddings and knowledge graphs,” in CVPR 2018, 2018, pp. 6857–6866.

[95]C.-W. Lee, W. Fang, C.-K. Yeh, and Y.-C. F. Wang, “Multi-label zero-shot learning with structured knowledge graphs,” arXiv preprint arXiv:1711.06526, 2017.
[96]K. Marino, R. Salakhutdinov, and A. Gupta, “The more you know: Using knowledge graphs for image classification,” arXiv preprint arXiv:1612.04844, 2016.

[97]D. Teney, L. Liu, and A. van den Hengel, “Graph-structured representations for visual question answering,” arXiv preprint, 2017.

[98]M. Narasimhan, S. Lazebnik, and A. Schwing, “Out of the box: Reasoning with graph convolution nets for factual visual ques-tion answering,” in NeurIPS 2018, 2018, pp. 2659–2670.
[99]H. Hu, J. Gu, Z. Zhang, J. Dai, and Y. Wei, “Relation networks for object detection,” in CVPR 2018, vol. 2, no. 3, 2018.

[100]J. Gu, H. Hu, L. Wang, Y. Wei, and J. Dai, “Learning region features for object detection,” arXiv preprint arXiv:1803.07066, 2018.
[101]S. Qi, W. Wang, B. Jia, J. Shen, and S.-C. Zhu, “Learning human-object interactions by graph parsing neural networks,” arXiv preprint arXiv:1808.07962, 2018.

[102]A. Jain, A. R. Zamir, S. Savarese, and A. Saxena, “Structural-rnn: Deep learning on spatio-temporal graphs,” in CVPR 2016, 2016,
ap.5308–5317.
[103]X. Chen, L.-J. Li, L. Fei-Fei, and A. Gupta, “Iterative visual reasoning beyond convolutions,” arXiv preprint arXiv:1803.11189, 2018.

[104]X. Liang, L. Lin, X. Shen, J. Feng, S. Yan, and E. P. Xing, “Interpretable structure-evolving lstm,” in CVPR 2017, 2017, pp. 2175–2184.

[105]L. Landrieu and M. Simonovsky, “Large-scale point cloud se-mantic segmentation with superpoint graphs,” arXiv preprint arXiv:1711.09869, 2017.

[106]Y. Wang, Y. Sun, Z. Liu, S. E. Sarma, M. M. Bronstein, and J. M. Solomon, “Dynamic graph cnn for learning on point clouds,” arXiv preprint arXiv:1801.07829, 2018.

[107]X. Qi, R. Liao, J. Jia, S. Fidler, and R. Urtasun, “3d graph neural networks for rgbd semantic segmentation,” in CVPR 2017, 2017,
ap.5199–5208.
[108]M. Zitnik, M. Agrawal, and J. Leskovec, “Modeling polyphar-macy side effects with graph convolutional networks,” arXiv preprint arXiv:1802.00543, 2018.

[109]S. Rhee, S. Seo, and S. Kim, “Hybrid approach of relation network and localized graph convolutional filtering for breast cancer subtype classification,” arXiv preprint arXiv:1711.05859, 2017.

[110]Z. Wang, Q. Lv, X. Lan, and Y. Zhang, “Cross-lingual knowledge graph alignment via graph convolutional networks,” in EMNLP 2018, 2018, pp. 349–357.

[111]A. Nowak, S. Villar, A. S. Bandeira, and J. Bruna, “Revised note on learning quadratic assignment with graph neural networks,” in IEEE DSW 2018. IEEE, 2018, pp. 1–5.

[112]Z. Li, Q. Chen, and V. Koltun, “Combinatorial optimization with graph convolutional networks and guided tree search,” in NeurIPS 2018, 2018, pp. 537–546.

[113]W. Kool and M. Welling, “Attention solves your tsp,” arXiv preprint arXiv:1803.08475, 2018.
[114]A. Bojchevski, O. Shchur, D. Zugner,¨ and S. Gunnemann,¨ “Netgan: Generating graphs via random walks,” arXiv preprint arXiv:1803.00816, 2018.

[115]T. Ma, J. Chen, and C. Xiao, “Constrained generation of semanti-cally valid graphs via regularizing variational autoencoders,” in NeurIPS 2018, 2018, pp. 7113–7124.

[116]J. You, B. Liu, R. Ying, V. Pande, and J. Leskovec, “Graph convolutional policy network for goal-directed molecular graph generation,” arXiv preprint arXiv:1806.02473, 2018.

[117]N. De Cao and T. Kipf, “Molgan: An implicit generative model for small molecular graphs,” arXiv preprint arXiv:1805.11973, 2018.

[118]Z. Cui, K. Henrickson, R. Ke, and Y. Wang, “Traffic graph con-volutional recurrent neural network: A deep learning framework for network-scale traffic learning and forecasting,” 2018.

[119]R. van den Berg, T. N. Kipf, and M. Welling, “Graph convolu-tional matrix completion,” arXiv preprint arXiv:1706.02263, 2017.

[120]R. Ying, R. He, K. Chen, P. Eksombatchai, W. L. Hamilton, and J. Leskovec, “Graph convolutional neural networks for web-scale recommender systems,” arXiv preprint arXiv:1806.01973, 2018.

[121]Z. Ying, J. You, C. Morris, X. Ren, W. Hamilton, and J. Leskovec, “Hierarchical graph representation learning with differentiable pooling,” in NeurIPS 2018, 2018, pp. 4805–4815.

[122]M. Allamanis, M. Brockschmidt, and M. Khademi, “Learning to represent programs with graphs,” arXiv preprint arXiv:1711.00740, 2017.

[123]O. Russakovsky, J. Deng, H. Su, J. Krause, S. Satheesh, S. Ma, Z. Huang, A. Karpathy, A. Khosla, M. Bernstein et al., “Imagenet large scale visual recognition challenge,” IJCV 2015, vol. 115, no. 3, pp. 211–252, 2015.

[124]W. Norcliffe-Brown, S. Vafeias, and S. Parisot, “Learning condi-tioned graph structures for interpretable visual question answer-ing,” in NeurIPS 2018, 2018, pp. 8344–8353.

[125]J. You, R. Ying, X. Ren, W. Hamilton, and J. Leskovec, “Graphrnn: Generating realistic graphs with deep auto-regressive models,” in ICML 2018, 2018, pp. 5694–5703.

20

[126]Y. Li, O. Vinyals, C. Dyer, R. Pascanu, and P. Battaglia, “Learning deep generative models of graphs,” arXiv preprint arXiv:1803.03324, 2018.

[127]I. Bello, H. Pham, Q. V. Le, M. Norouzi, and S. Bengio, “Neural combinatorial optimization with reinforcement learning,” arXiv preprint arXiv:1611.09940, 2016.

[128]O. Vinyals, M. Fortunato, and N. Jaitly, “Pointer networks,” in NIPS 2015, 2015, pp. 2692–2700.

[129]R. S. Sutton and A. G. Barto, Reinforcement learning: An introduc-tion. MIT press, 2018.

[130]E. Khalil, H. Dai, Y. Zhang, B. Dilkina, and L. Song, “Learning combinatorial optimization algorithms over graphs,” in NIPS 2017, 2017, pp. 6348–6358.