多项式回归的Python实现

设多项式 $f_\theta (x)=\theta _0+\theta _1x+\theta _2x^{2}$

将参数和训练数据都作为向量来处理，可以使计算变得更简单。

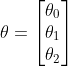
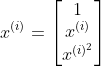
$\theta =\begin{bmatrix} \theta _0\ \theta _1\ \theta _2\end{bmatrix}$ $x^{(i)}=\begin{bmatrix} 1\ x^{(i)}\ x^{(i)^{2}}\end{bmatrix}$

由于训练数据有很多，所以我们把1 行数据当作1 个训练数据，以矩阵的形式来处理会更好。

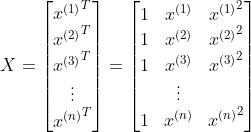
$X=\begin{bmatrix} {x^{(1)}}^{T}\ {x^{(2)}}^{T}\ {x^{(3)}}^{T}\ \vdots \ {x^{(n)}}^{T}\end{bmatrix}=\begin{bmatrix} 1 & x^{(1)}& {x^{(1)}}^{2}\ 1 & x^{(2)} & {x^{(2)}}^{2}\ 1 & x^{(3)}& {x^{(3)}}^{2}\ & \vdots & \ 1& x^{(n)}& {x^{(n)}}^{2} \end{bmatrix}$

矩阵与参数向量θ 的积如下

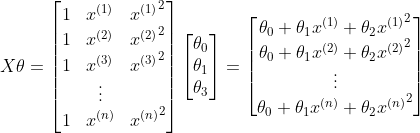
$X\theta =\begin{bmatrix} 1 & x^{(1)}& {x^{(1)}}^{2}\ 1 & x^{(2)} & {x^{(2)}}^{2}\ 1 & x^{(3)}& {x^{(3)}}^{2}\ & \vdots & \ 1& x^{(n)}& {x^{(n)}}^{2} \end{bmatrix}\begin{bmatrix} \theta _0\ \theta _1 \ \theta _3 \end{bmatrix}=\begin{bmatrix} \theta _0+\theta _1x^{(1)}+{\theta _2x^{(1)}}^{2}\ \theta _0+\theta _1x^{(2)}+{\theta _2x^{(2)}}^{2}\ \vdots \\theta _0+\theta _1x^{(n)}+{\theta _2x^{(n)}}^{2} \end{bmatrix}$

在Jupyter Notebook中表示

#初始化
theta = np.random.rand(3)#通过np.random.randn(d0,d1,d2……dn)函数可以返回一个或一组服从“0~1”均匀分布的随机样本值。随机样本取值范围是[0,1)，不包括1。
#创建训练数据的矩阵
def to_matrix(x):
    return np.vstack([np.ones(x.shape[0]), x, x**2]).T#ones()返回一个全1的n维数组，同样也有三个参数：shape（用来指定返回数组的大小）、dtype（数组元素的类型）,np.vstack():在竖直方向上堆叠

X = to_matrix(train_z)
#预测函数
def f(x):
    return np.dot(x, theta)

参数更新表达式，在我前面的博客里面，多重回归时有讲到推理过程

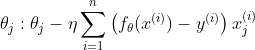
$\theta _j:\theta _j-\eta \sum_{i=1}^{n}\left ( f_\theta (x^{(i)})-y^{(i)} \right )x_j^{(i)}$

这里很容易让人想到用循环来实现，但其实如果好好利用训练数据的矩阵X，就能一下子全部计算出来。比如在j = 0 的时候，把更新表达式的Σ部分展开，就会变成这样子。

$(f_\theta (x^{(1)})-y^{(1)})x_0^{(1)}+(f_\theta (x^{(2)})-y^{(2)})x_0^{(2)}+\cdots$

把表达式中 $f_\theta (x^{(i)})-y^{(i)}$ 和 $x_0^{(i)}$ 的部分分别当作向量来处理

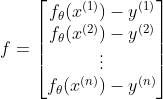
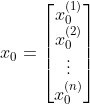
$f=\begin{bmatrix} f_\theta(x^{(1)}) -y^{(1)}\ f_\theta (x^{(2)})-y^{(2)}\ \vdots \ f_\theta (x^{(n)})-y^{(n)}\end{bmatrix}$ $x_0=\begin{bmatrix} x_0^{(1)}\ x_0^{(2)}\ \vdots \ x_0^{(n)}\end{bmatrix}$

j=0时把f 转置之后与 $x_0$ 相乘，就与和的部分一样了。

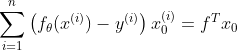
$\sum_{i=1}^{n}\left ( f_\theta (x^{(i)})-y^{(i)} \right )x_0^{(i)}=f^{T}x_0$

现在 $x_0^{(i)}$ 全部为1， $x_1^{(i)}$ 为 $x^{(i)}$ 、 $x_2^{(i)}$ 为 ${x^{(i)}}^{2}$

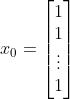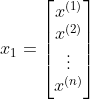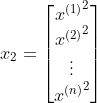
$x_0=\begin{bmatrix} 1\ 1\ \vdots \ 1\end{bmatrix}$ , $x_1=\begin{bmatrix} x^{(1)}\ x^{(2)}\ \vdots \x^{(n)}\end{bmatrix}$ , $x_2=\begin{bmatrix} {x^{(1)}}^{2}\ {x^{(2)}}^{2}\ \vdots \{x^{(n)}}^{2}\end{bmatrix}$

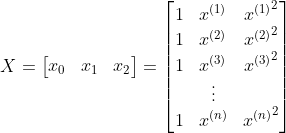
$X=\begin{bmatrix} x_0 &x_1 &x_2 \end{bmatrix}=\begin{bmatrix} 1 & x^{(1)}&{x^{(1)}} ^{2}\ 1 & x^{(2)}&{x^{(2)}} ^{2}\ 1 & x^{(3)}&{x^{(3)}} ^{2} \ & \vdots & \ 1 & x^{(n)}&{x^{(n)}} ^{2} \end{bmatrix}$

$f^{T}X$ 就能一次性地更新θ 了

#误差的差值
diff = 1
#重复学习
error = E(X,train_y)
while diff>1e-2:
    #更新参数
    theta = theta - ETA*np.dot(f(X)-train_y,X)
    #计算与上一次误差的差值
    current_error = E(X, train_y)
    diff = error - current_error
    error = current_error
x = np.linspace(-3, 3, 100)
plt.plot(train_z, train_y, 'o')
plt.plot(x, f(to_matrix(x)))
plt.show()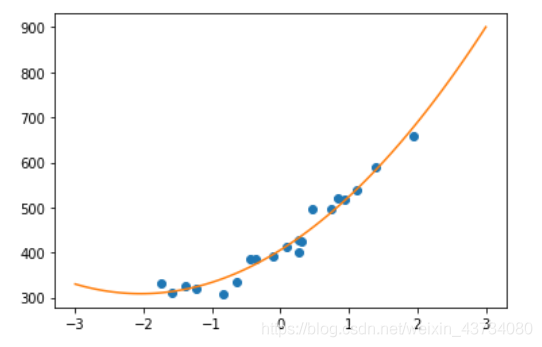

从上图可以发现，拟合了训练数据的曲线。以重复次数为横轴、均方误差为纵轴来绘图，来观察曲线不断下降的样子。

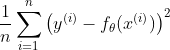
$\frac{1}{n}\sum_{i=1}^{n}\left ( y^{(i)}-f_\theta (x^{(i)}) \right )^{2}$

在停止重复的条件里可以用上均方误差

#均方误差
def MSE(x, y):
    return (1 / x.shape[0])*np.sum((y-f(x))**2)#x.shape(0)指行数
#用随机值初始化参数
theta = np.random.rand(3)
#均方差的历史记录
errors = []
#误差的差值
diff = 1
#重复学习
errors.append(MSE(X, train_y))
while diff>1e-2:
    theta = theta - ETA*np.dot(f(X) - train_y, X)
    errors.append(MSE(X, train_y))
    diff = errors[-2] - errors[-1]
#绘制误差变化图
x = np.arange(len(errors))
plt.plot(x, errors)
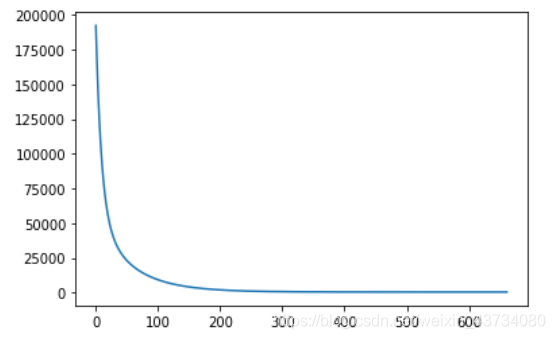
plt.show()

结果如下图，我们不难发现误差在不断下降

原文链接：https://blog.csdn.net/weixin_43734080/article/details/118879928