小波变换原理_小波变换1：基础介绍

本文主要介绍小波分析的相关内容，小波分析在声发射中的应用后面再讲。本文所记录内容主要是傅里叶变换、傅里叶变换分析非平稳信号的不足、小波变换的相对优势、什么是小波变换。本文默认您已经学习过高等数学的相关知识，知道傅里叶变换的原理和概念、了解时域/频域的概念。

1、傅里叶变换

傅里叶变换是将一个时域信号用不同频率/相位的三角波函数进行拟合。过程如上图所示，最左边的是原始信号，右边是不同频率的三角波信号，不同频率的三角波信号叠加之后可以近似拟合成原始信号。

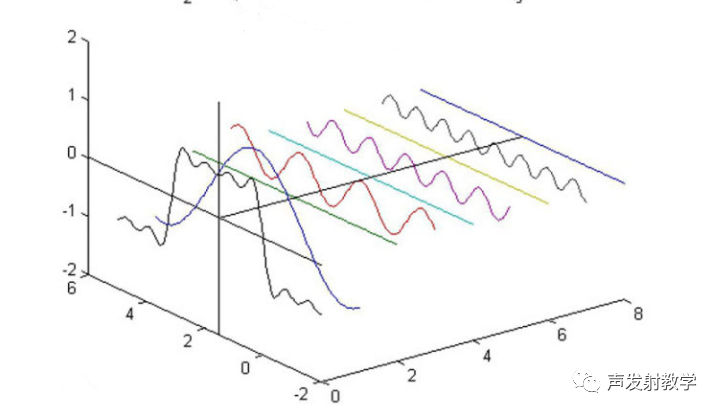
从正面看有人如下图所示

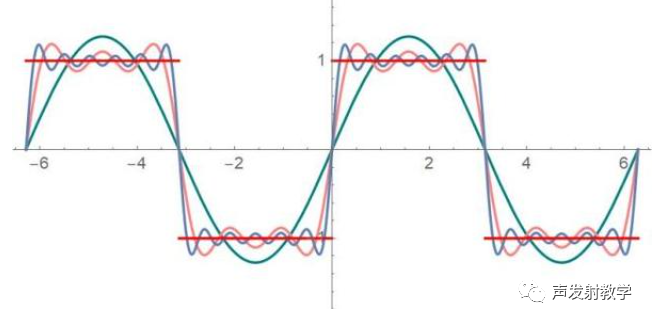
2、傅里叶变换分析非平稳信号的不足

如下图所示，左上的信号是50/120Hz信号在幅度上的叠加，右上是50/120Hz信号在时间上的叠加当时在两者的频率谱上是发现不小区别的。就是说傅里叶变换的时间分辨率很差。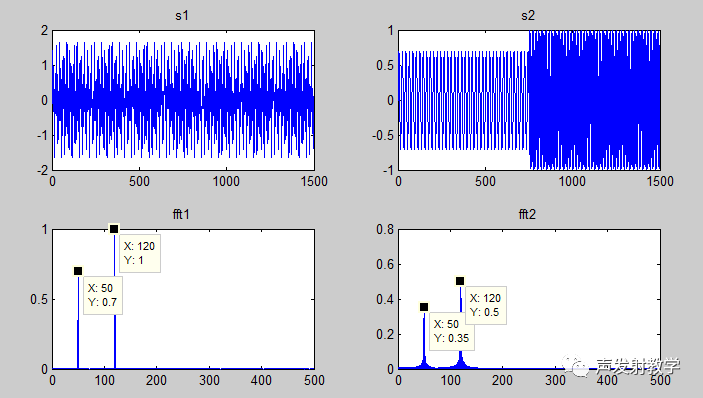

3、小波变换的优势

我们用小波变换分解一下波形，下图1是S1的分解，下图2是S2的分解，能够在时域上很清晰的看到频率的变化。声发射信号通常都是非平稳的信号，所以小波变换相比于傅里叶变换在某些时候要更有助于信号的分析。

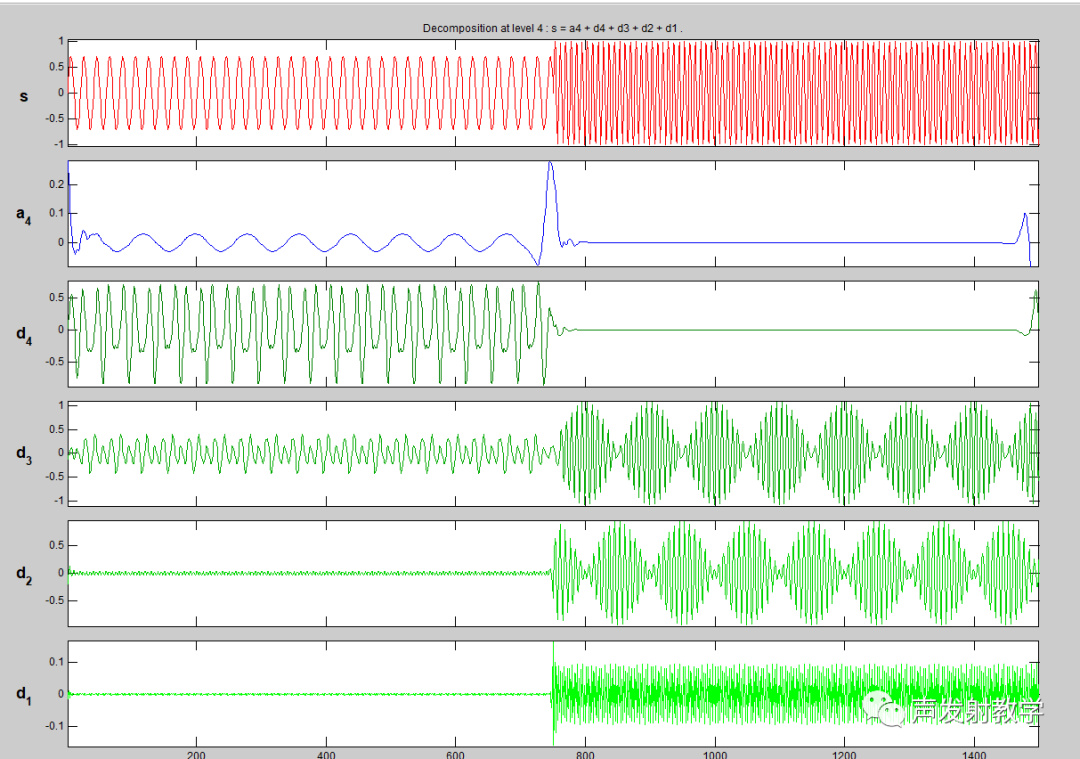
4、小波变换的原理

小波变换其实使用一个小波基取代了傅里叶变换中的三角函数。如下图，小波基是一个中间震荡，双边衰减的波形，可以对其进行缩放拉伸，之后拟合会原始波形。这样就会得到两个参数，一个是Y轴的压缩，一个是X轴的位移，正式X轴的位移让其具有了很高的时间上的频率分辨能力。

以上

如果您在文章末尾看到广告，麻烦动动手指点击一下，谢谢！