本文将总结 强化学习中的一个重要基础知识,Bellman Equation。
文章目录
符号定义
- π \piπ:函数符号,表示策略(Policy)函数,参数常为环境返回的状态,输出为一个具体的动作,可知a = π ( s ) ∈ A a = \pi ( s ) \in Aa=π(s)∈A
- r rr:执行动作a aa 后所获取的即时奖励,r t r_trt 表示t时刻所获取即时奖励。
- G GG:累积奖赏,G t G_tGt 表示从t时刻到一轮episode结束累积奖赏。
- E [ . ] E[.]E[.]: 表示计算期望。
value based 方法
首先了解一下何为 强化学习中的value based 方法,我们知道Agent的目标是:在生命周期内,执行一个序列的action,且该序列(马尔科夫奖励链)a c t i o n actionaction 所获取的r e w a r d rewardreward 之和(可以是加上discount factor γ \gammaγ 之后的求和)能达到最大。例如在时刻t tt 时,Agent在马尔科夫奖励链上从t tt 时刻以后未来所有有衰减的累积奖励(折现的奖励)总和。 如下:
G t = r t + 1 + γ r t + 2 + γ 2 r t + 3 + . . . = ∑ j = 0 T γ j r t + j + 1 G_t = r_{t+1} + \gamma r_{t+2} + \gamma^2 r_{t+3} + ...=\sum_{j=0}^{T} \gamma^j r_{t+j+1}Gt=rt+1+γrt+2+γ2rt+3+...=j=0∑Tγjrt+j+1
上式中,如果γ = 0 \gamma = 0γ=0,则表示Agent放弃长远的收益,而只在乎即时的r e w a r d rewardreward,同理如果γ = 1 \gamma = 1γ=1,则表示Agent将长远收益和当前即时收益放在同等重要位置。通常情况下γ ∈ ( 0 , 1 ) \gamma \in (0,1)γ∈(0,1),也即是当γ > 0 \gamma >0γ>0 时,是非贪心的。
可以重写上述公式如下:
G t = r t + 1 + γ r t + 2 + γ 2 r t + 3 + . . . + γ T − 1 r T G_t = r_{t+1} + \gamma r_{t+2} + \gamma^2 r_{t+3} +...+\gamma^{T-1} r_{T}Gt=rt+1+γrt+2+γ2rt+3+...+γT−1rT
= r t + 1 + γ ( r t + 2 + γ r t + 3 + . . . + γ T − 2 r T ) =r_{t+1} + \gamma(r_{t+2} + \gamma r_{t+3}+...+\gamma^{T-2} r_{T})=rt+1+γ(rt+2+γrt+3+...+γT−2rT)
= r t + 1 + γ ( G t + 1 ) = r_{t+1} + \gamma (G_{t+1})=rt+1+γ(Gt+1)
这样就可以通过递归的形式计算G
大部分强化学习算法都涉及到估计 状态价值函数(Value Function),该函数的自变量为 状态 或 状态-动作对,这种称为基于值的学习,也即 value-based。
通常情况下,时刻t后执行序列可能有多条 马尔科夫奖励,我们需要使用状态价值函数来评估状态s ss 的长期价值。
马尔科夫奖励(Markov Reward Process,MRP)过程定义式如下:
是一个由 < S , P , R , γ > <S, P, R, \gamma><S,P,R,γ> 组成的元组(tuple):
S SS 是有限的状态
P PP 是状态转移概率矩阵 P s s ′ = P ( S t + 1 = S ′ ∣ S t = S ) P_{ss'} = P(S_{t+1} = S'|S_t = S)Pss′=P(St+1=S′∣St=S)
R RR 是奖励函数 R s = E [ R t + 1 ∣ S t = s ] R_s = E[R_{t+1}|S_t=s]Rs=E[Rt+1∣St=s]
γ \gammaγ 是衰减系数,γ ∈ [ 0 , 1 ] \gamma \in [0,1]γ∈[0,1]
The V-function: the value of the state
V-function 可以称为状态价值函数,当Agent遵循策略π \piπ 时,根据return G(累积奖赏),评估某个特定状态的好坏。也就是v − f u n c t i o n v-functionv−function 可以定义为从state开始的未来累积奖赏期望值。故V-function 可表示如下:
v π ( s ) = E π [ G t ∣ s = s t ] = E π [ ∑ j = 0 T γ j r t + j + 1 ∣ s = s t ] v_{\pi}(s)=E_{\pi}[G_t|s=s_t] = E_{\pi}[\sum_{j=0}^{T} \gamma^{j}r_{t+j+1}|s=s_t]vπ(s)=Eπ[Gt∣s=st]=Eπ[j=0∑Tγjrt+j+1∣s=st]
注意v-function自变量是状态s ss
为了更好的理解V − f u n c t i o n V-functionV−function,这里以只有三个状态的环境举例:
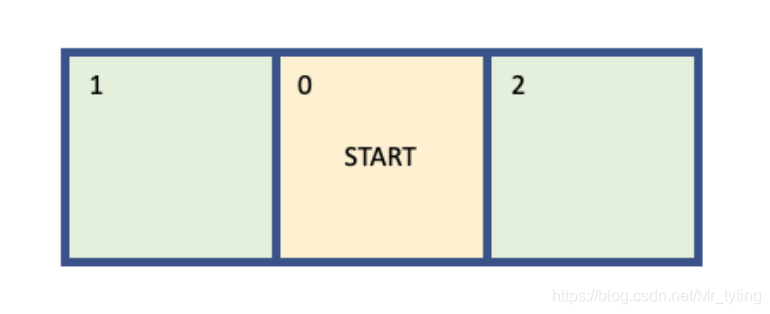
定义reward:
- 初始在0状态上
- 当从状态0向左移动时,变成状态1,reward += 1
- 当从状态0向右移动时,变成状态2,reward += 2
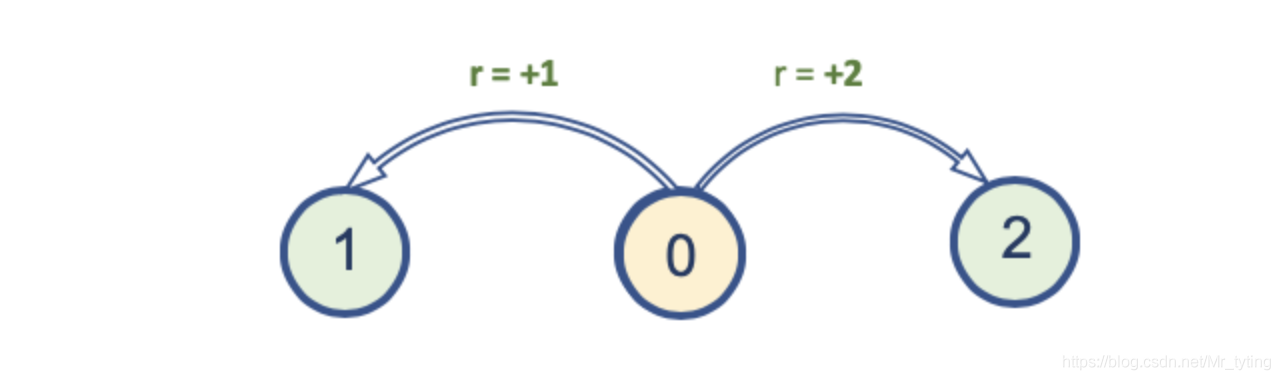
上述环境始终是确定的,每一个episode都是从状态0开始,当到达状态1或者状态2时,该episode结束。
现在的问题是V ( 0 ) V(0)V(0) 是多少?根据上面讲到的v − f u n c t i o n v-functionv−function 公式:
v π ( s ) = E π [ ∑ j = 0 T γ j r t + j + 1 ∣ s = s t ] v_{\pi}(s)= E_{\pi}[\sum_{j=0}^{T} \gamma^{j}r_{t+j+1}|s=s_t]vπ(s)=Eπ[j=0∑Tγjrt+j+1∣s=st]
可知V ( 0 ) V(0)V(0) 也与策略(policy)π \piπ 关系很大,例如有如下策略:
- 策略1:Agent始终向左
- 策略2:Agent始终向右
- 策略3:Agent向左移动概率为0.5,向右移动概率为0.5
- 策略4:Agent向左移动概率为0.2,向右移动概率为0.8
分别根据以上policy计算一个e p i s o d e episodeepisode 的V ( 0 ) V(0)V(0):
- 策略1:V ( 0 ) = 1 V(0) = 1V(0)=1
- 策略2:V ( 0 ) = 2 V(0) = 2V(0)=2
- 策略3:V ( 0 ) = 0.5 ∗ 1 + 0.5 ∗ 2 = 1.5 V(0) = 0.5*1+0.5*2 = 1.5V(0)=0.5∗1+0.5∗2=1.5
- 策略4:V ( 0 ) = 0.2 ∗ 1 + 0.8 ∗ 2 = 1.8 V(0) = 0.2*1+0.8*2 = 1.8V(0)=0.2∗1+0.8∗2=1.8
为了能是t o t a l r e w a r d total\ rewardtotal reward 尽可能的大,对于Agent来说,最优的policy是策略2,也即始终向右移动。
上述简单的环境,让人误以为采用 “贪婪”策略,能得到收益最大的reward。然而对于较为复杂的环境并非如此,例如下面有四个状态的环境: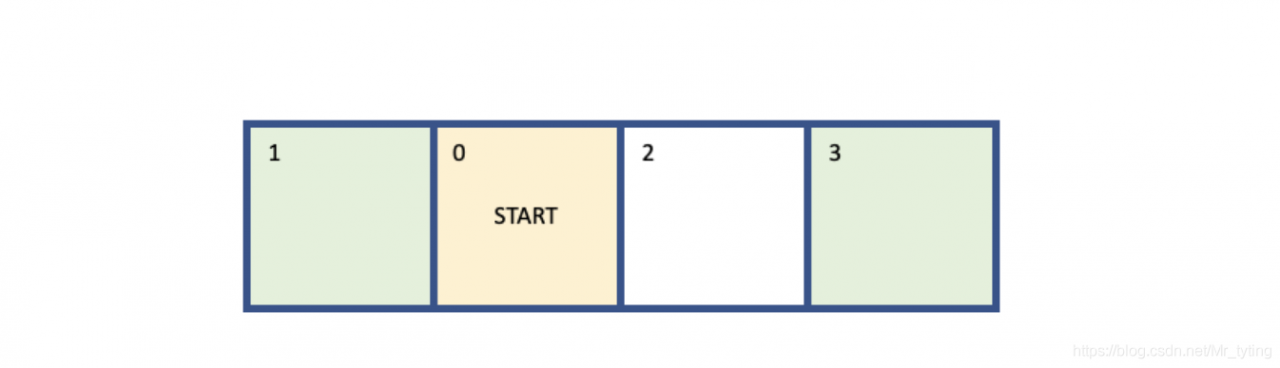
同上面一样,每次都是从状态0开始,当到达边界是,一个episode结束,reward变化如下: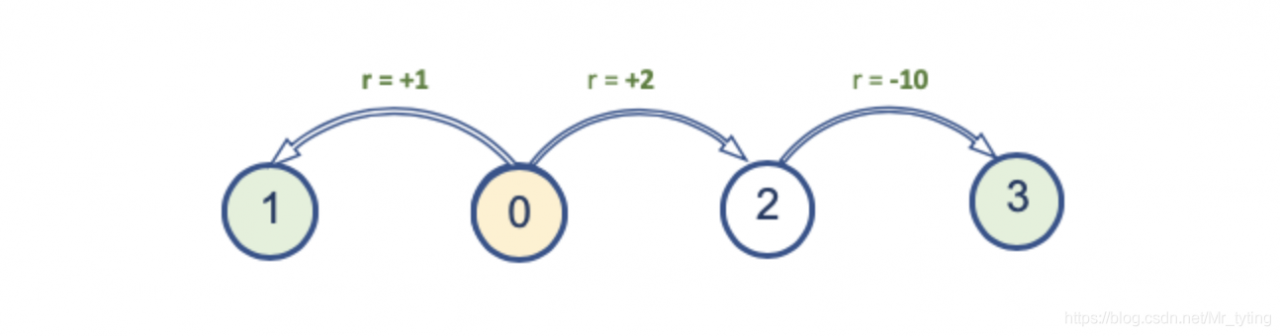
显然这时,每个策略的V ( 0 ) V(0)V(0) 如下:
- 策略1:V ( 0 ) = 1 V(0)=1V(0)=1
- 策略2:V ( 0 ) = 2 − 10 = − 8 V(0) = 2-10=-8V(0)=2−10=−8
- 策略3:V ( 0 ) = 1.0 ∗ 0.5 + ( 2 − 10 ) ∗ 0.5 = − 3.5 V(0)=1.0*0.5+(2-10)*0.5 = -3.5V(0)=1.0∗0.5+(2−10)∗0.5=−3.5
- 策略4:V ( 0 ) = 1.0 ∗ 0.2 + ( 2 − 10 ) ∗ 0.8 = − 6.2 V(0) = 1.0*0.2+(2-10)*0.8 = -6.2V(0)=1.0∗0.2+(2−10)∗0.8=−6.2
显然这时候,策略1的收益最大,而策略2的收益最小了。
The Q-function: The value of the action
我们将状态价值函数,扩展到状态-行动对,为每个状态-行动 对 定义一个值,该值为行动价值函数。该函数表示Agent在遵循策略π \piπ情况下,在状态s ss下,执行动作a aa的预计获取累积奖赏的期望值,用Q π ( s , a ) Q_{\pi}(s,a)Qπ(s,a)。
Q π ( s , a ) = E π [ G t ∣ S t = s , A t = a ] = E π [ ∑ j = 0 T γ j r t + j + 1 ∣ S t = s , A t = a ] Q_{\pi}(s,a)=E_{\pi}[G_t|S_t=s, A_t=a]=E_{\pi}[\sum_{j=0}^{T} \gamma^j r_{t+j+1}|S_t=s, A_t=a]Qπ(s,a)=Eπ[Gt∣St=s,At=a]=Eπ[j=0∑Tγjrt+j+1∣St=s,At=a]
我们再来定义policy在状态s ss 下 执行动作a aa 的概率为π ( a ∣ s ) \pi(a|s)π(a∣s),则有
∑ a π ( a ∣ s ) = 1 \sum_a \pi(a|s) = 1a∑π(a∣s)=1
这就引入了动作概率,也即策略函数。
再来看看 Q-function 和 V-function 的关系:
V π ( s ) = ∑ a π ( a ∣ s ) ⋅ Q π ( s , a ) V_{\pi}(s) = \sum_a \pi(a|s) \cdot Q_{\pi} (s,a)Vπ(s)=a∑π(a∣s)⋅Qπ(s,a)
马尔可夫决策过程(Markov decision process,MDP)是在马尔可夫奖励(MRP)过程的基础上增加了决策(decisions/actions),是一个由< S , A , P , R , γ > <S,A,P,R, \gamma><S,A,P,R,γ>组成的元组(tuple):
S SS 是有限的状态
A AA 是有限的决策/动作集
P PP 是状态转移概率矩阵 P s s ′ a = P ( S t + 1 = S ′ ∣ S t = S , A t = a ) P_{ss'}^a = P(S_{t+1} = S'|S_t = S, A_t=a)Pss′a=P(St+1=S′∣St=S,At=a)
R RR 是奖励函数 R s = E [ R t + 1 ∣ S t = s , A t = a ] R_s = E[R_{t+1}|S_t=s, A_t=a]Rs=E[Rt+1∣St=s,At=a]
γ \gammaγ 是衰减系数,γ ∈ [ 0 , 1 ] \gamma \in [0,1]γ∈[0,1]
The Bellman Equation
贝尔曼方程(Bellman Equation)在强化学习文献中随处可见,是许多强化学习算法的核心要素之一。我们可以说,贝尔曼方程将价值函数分解为两部分,即即时reward和未来value(经过discounted)。
也即
V ( s t ) = E π [ ∑ j = 0 T γ j r t + j + 1 ∣ s = s t ] = E [ R t + 1 + γ V ( s t + 1 ) ∣ s t = s ] V(s_t) = E_{\pi}[\sum_{j=0}^{T} \gamma^{j}r_{t+j+1}|s=s_t] = E[R_{t+1}+\gamma V(s_{t+1})|s_t = s]V(st)=Eπ[j=0∑Tγjrt+j+1∣s=st]=E[Rt+1+γV(st+1)∣st=s]
上述公式就是贝尔曼方程(Bellman Equation)
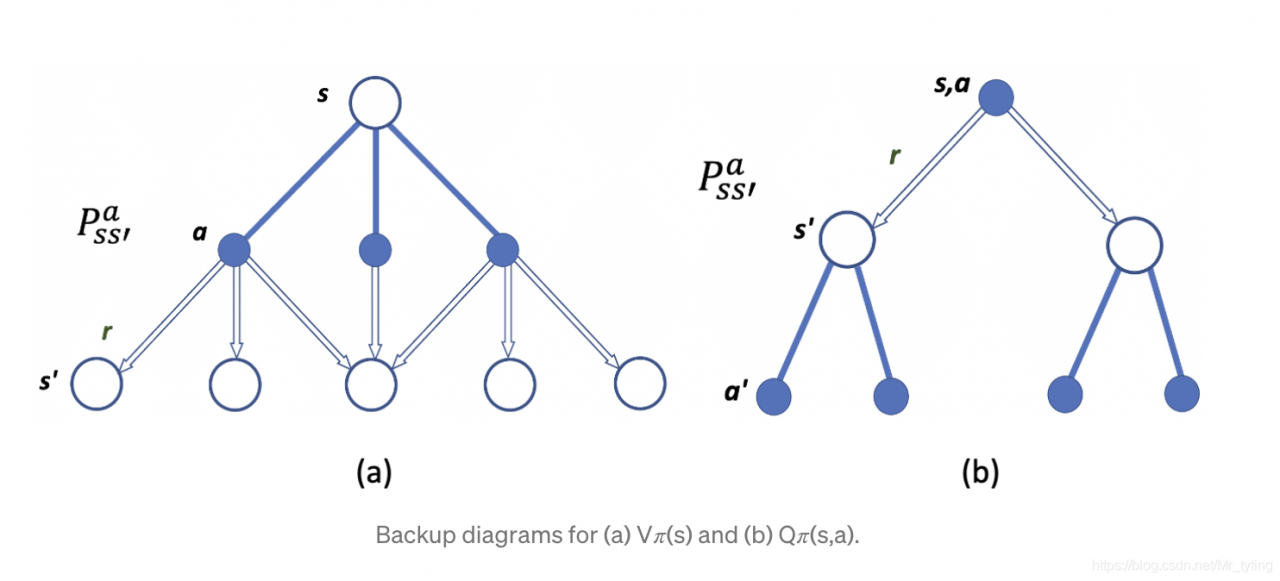
为了更好的说明 Bellman Equation,以上图进行举例,上图中P PP 表示在状态s ss 下执行动作a aa,得到状态s ′ s's′ 的概率(with reward r)。
Bellman equation for the State-value function
我们以贝尔曼方程(Bellman Equation)来表示 State-value function,如下:
V π ( s ) = ∑ a π ( a ∣ s ) ⋅ ∑ s ′ P s s ′ a ( r ( s , a ) + γ V π ( s ′ ) ) V_{\pi}(s) = \sum_a \pi(a|s) \cdot \sum_{s'} P^{a}_{ss'}(r(s,a)+\gamma V_{\pi}(s'))Vπ(s)=a∑π(a∣s)⋅s′∑Pss′a(r(s,a)+γVπ(s′))
Bellman equation for the Action-value function
同样的,也可以以贝尔曼方程(Bellman Equation)来表示 Action-value function,如下:
Q π = ∑ s ′ P s s ′ a ( r ( s , a ) + γ ⋅ ∑ a ′ π ( a ′ ∣ s ′ ) ⋅ Q π ( s ′ , a ′ ) ) = ∑ s ′ P s s ′ a ( r ( s , a ) + γ V π ( s ′ ) ) Q_{\pi} = \sum_{s'}P^{a}_{ss'}(r(s,a)+\gamma \cdot \sum_{a'} \pi(a'|s') \cdot Q_{\pi}(s', a'))= \sum_{s'}P^{a}_{ss'}(r(s,a) + \gamma V_{\pi}(s'))Qπ=s′∑Pss′a(r(s,a)+γ⋅a′∑π(a′∣s′)⋅Qπ(s′,a′))=s′∑Pss′a(r(s,a)+γVπ(s′))
Optimal Policy
上面说过,Agent学习的目的是使得total reward最大化,现在我们就需要求解total reward最大时的策略 π ∗ \pi^*π∗,那么这个π ∗ \pi^*π∗ 如何定义呢?
- 对于所有的s t a t e statestate s ss,V π ∗ ( s ) ≥ V π ( s ) ∀ π V_{\pi^*}(s) \geq V_{\pi}(s)\ \forall \piVπ∗(s)≥Vπ(s) ∀π
显然符合上述条件的π ∗ \pi^*π∗ 不一定是唯一的,可以存在多个。
则最优状态价值函数为:
V ∗ ( s ) = m a x π V π ( s ) V_{*}(s)=max_{\pi}V_{\pi}(s)V∗(s)=maxπVπ(s)
上述公式表示,寻找一个最优策略π \piπ,使得V ( s ) V(s)V(s) 能达到最大,也即是Agent沿着策略π ∗ \pi^*π∗,在状态s ss 能获得最大的累积期望奖励。
同样的对于最优动作价值函数为:
Q ∗ ( s , a ) = m a x π Q π ( s , a ) Q_{*}(s,a)=max_{\pi} Q_{\pi}(s,a)Q∗(s,a)=maxπQπ(s,a)
上述公式表示,寻找一个最优策略π \piπ,使得Q ( s , a ) Q(s,a)Q(s,a) 能达到最大,也即是在状态s ss 下采用动作a aa 能获得最大的累积期望奖励。
上面提到的V ( s ) V(s)V(s) 与 Q ( s , a ) Q(s,a)Q(s,a) 转换公式:
V π ( s ) = ∑ a π ( a ∣ s ) ⋅ Q π ( s , a ) V_{\pi}(s) = \sum_a \pi(a|s) \cdot Q_{\pi} (s,a)Vπ(s)=a∑π(a∣s)⋅Qπ(s,a)
那么V ∗ ( s ) V_{*}(s)V∗(s) 与 Q ∗ ( s , a ) Q_{*}(s,a)Q∗(s,a) 转换公式如下:
V π ∗ ( s ) = ∑ a π ∗ ( a ∣ s ) ⋅ Q π ∗ ( s , a ) V_{\pi^*}(s) = \sum_a \pi^{*}(a|s) \cdot Q_{\pi^*} (s,a)Vπ∗(s)=a∑π∗(a∣s)⋅Qπ∗(s,a)
显然对于这样最优的π ∗ \pi^*π∗有:
π ∗ ( a ∣ s ) = { 1 i f a = a r g m a x a ∈ A Q π ∗ ( s , a ) 0 otherwise \pi^*(a|s)= \begin{cases} 1& if\ a = \underset {a \in A}{argmax} Q_{\pi^*}(s,a)\\ 0 & \text{otherwise} \end{cases}π∗(a∣s)=⎩⎨⎧10if a=a∈AargmaxQπ∗(s,a)otherwise
故有:
V π ∗ ( s ) = m a x a Q π ∗ ( s , a ) V_{\pi^*}(s) =max_{a} Q_{\pi^*} (s,a)Vπ∗(s)=maxaQπ∗(s,a)
The Bellman equation of optimality
通过上述的公式推导,我们可以进一步得到:
V ∗ ( s ) = m a x a ∑ s ′ P s s ′ a ( r ( s , a ) + γ V ∗ ( s ′ ) ) V_{*}(s) = \underset {a}{max} \sum_{s'} P^{a}_{ss'}(r(s,a)+\gamma V_{*}(s'))V∗(s)=amaxs′∑Pss′a(r(s,a)+γV∗(s′))
Q ∗ ( s , a ) = ∑ s ′ P s s ′ a ( r ( s , a ) + γ m a x a ′ Q ∗ ( s ′ , a ′ ) ) Q_{*}(s,a) = \sum_{s'} P^{a}_{ss'}(r(s,a)+\gamma \underset {a'}{max} Q_{*}(s', a'))Q∗(s,a)=s′∑Pss′a(r(s,a)+γa′maxQ∗(s′,a′))’
总结
- Q-Function 与 V-Function 的区别在于在当前时刻是否执行动作 a aa
- Bellman Equation 是一种动态规划方法,将最佳问题变成简单子问题
参考资料
- https://towardsdatascience.com/the-bellman-equation-59258a0d3fa7
- https://zhuanlan.zhihu.com/p/139791993