基于AR滤波器的轴承故障诊断
关于AR滤波器,可参考如下论文,其中AR滤波器的阶数选择非常重要
[1]从飞云,陈进,董广明.基于滚动轴承故障诊断的AR预测滤波器阶数问题研究[J].振动与冲击,2012,31(04):44-47.
首先,以一个简单的模拟信号开始。
fs = 1000;
t = 0:1/fs:1-1/fs;
x = cos(2*pi*10*t)+0.2*randn(size(t));
N = length(x);
%AR滤波
order = 512;%阶数
a =lpc(x,order);
x1 = filter([0 -a(2:end)],1,x);
x2 = x-x1;
其中,lpc是MATLAB线性预测函数。看一下预测结果及误差
figure
plot(t,x)
hold on
plot(t,x1)
xlabel('Time [s]')
ylabel('Magnitude')
legend('Original signal','LPC estimate');
setfontsize(14);
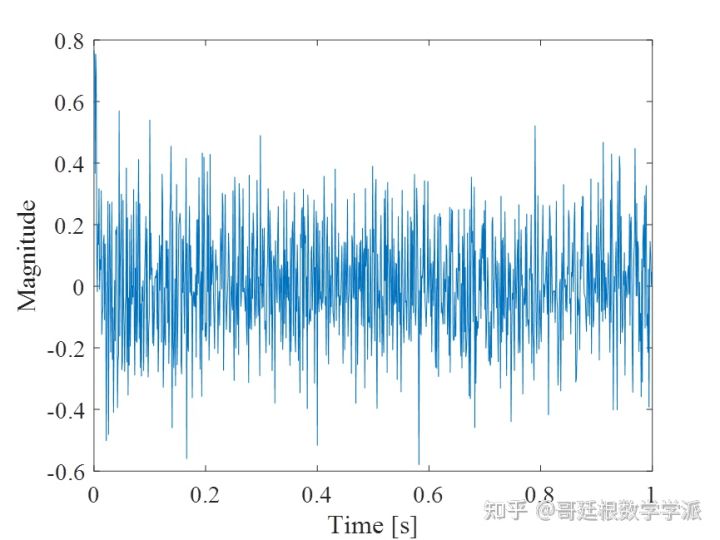
%误差
figure
plot(t,x2)
xlabel('Time [s]')
ylabel('Magnitude')
setfontsize(14);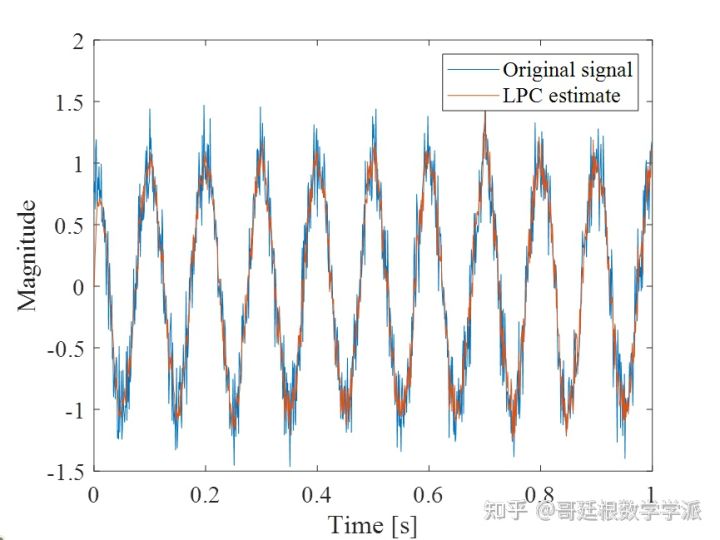
下面开始实际轴承故障诊断,轴承数据来源下面两篇文章
基于包络谱的轴承故障诊断方法-第1篇 - 哥廷根数学学派的文章 - 知乎 https://zhuanlan.zhihu.com/p/533579665
基于包络谱的轴承故障诊断方法-第2篇 - 哥廷根数学学派的文章 - 知乎 https://zhuanlan.zhihu.com/p/533984966
以第3个轴承Z轴70Hz第8组外圈故障信号为例,滤波器阶数首先设置为100
fs = 10240;
t = 1/10240:1/10240:1;
x1 = load('#8');x1 = x1.Z;x1 = x1(1:5120*2);x1 = x1-mean(x1);
x=x1;
BPFI = 6.587;
v = 70;
N = length(x);
%AR滤波
order = 100;
a =lpc(x,order);
x1 = filter([0 -a(2:end)],1,x);
x2 = x-x1;
%结果
figure(1)
plot(t,x)
% 线性预测系数LPC估计
hold on
plot(t,x1)
xlabel('Time [s]')
ylabel('Magnitude')
legend('Original signal','LPC estimate');
setfontsize(14);
figure(2)
subplot(2,1,1)
[pEnvInner, fEnvInner, xEnvInner, tEnvInner] = envspectrum(x, fs);plot(fEnvInner, pEnvInner)
xlim([0 800]);ncomb = 20;helperPlotCombs(ncomb,BPFI*v);xlabel('Frequency(Hz)');ylabel('Ampitude')
subplot(2,1,2)
[pEnvInner, fEnvInner, xEnvInner, tEnvInner] = envspectrum(x1, fs);plot(fEnvInner, pEnvInner)
xlim([0 800]);ncomb = 20;helperPlotCombs(ncomb,BPFI*v);xlabel('Frequency(Hz)');ylabel('Ampitude')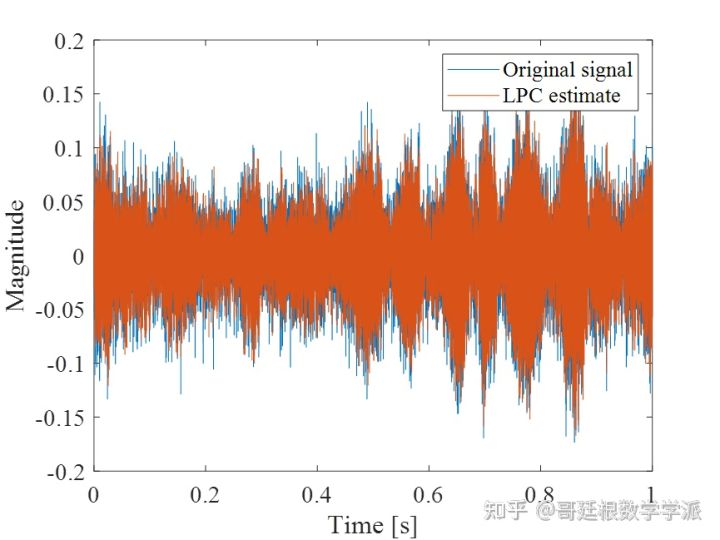
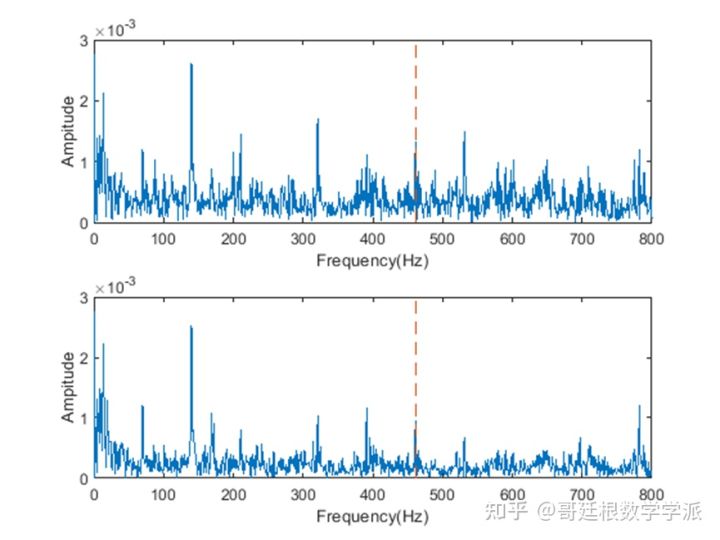
频谱上的噪声虽然一定程度上得到了抑制,但故障特征频率被没有得到有效突出。
滤波器阶数为300,500,800,1000时的结果分别如下
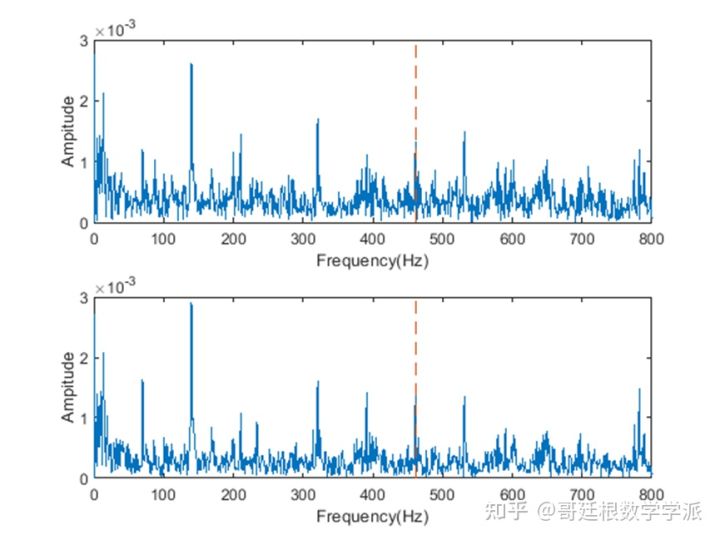
滤波器阶数300

滤波器阶数500
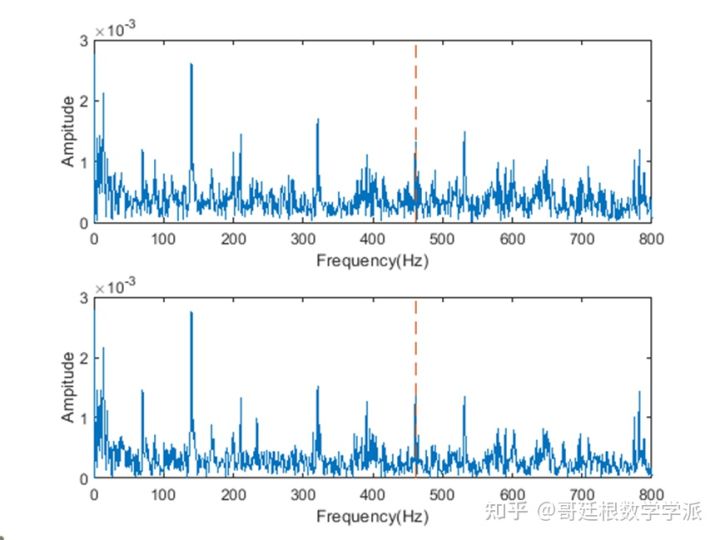
滤波器阶数800
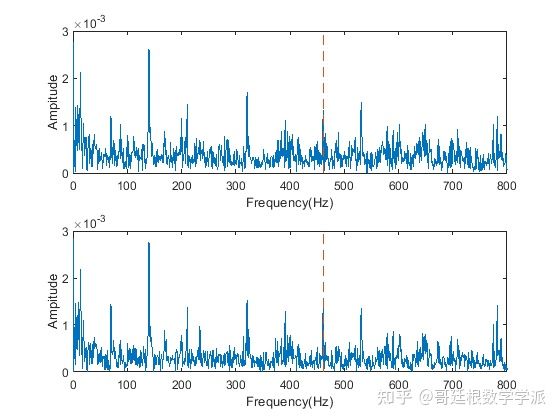
滤波器阶数1000
倒谱滤波
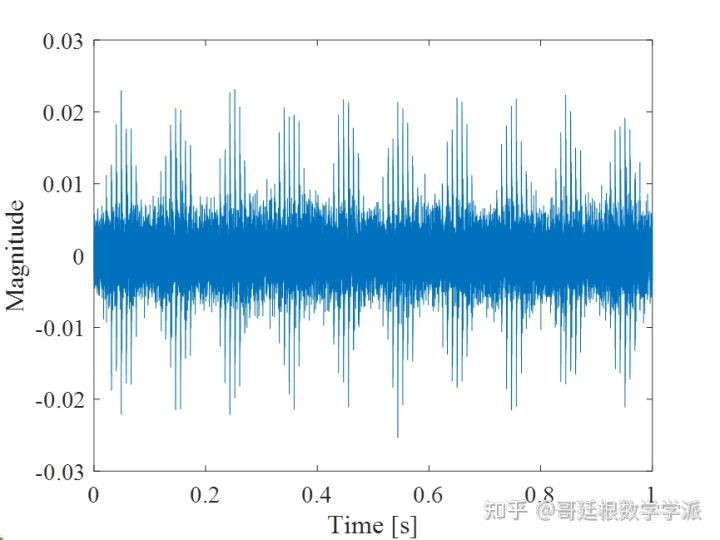
倒谱滤波原理非常简单,就一个公式而已,还是首先以一个模拟信号为例
load Cepstrum.mat;
fs = 24000;
N = length(x);
t = 0:1/fs:(N-1)/fs;
%倒谱滤波(变换)
y = real(ifft(log(abs(fft(x)))));%倒谱滤波就这一个公式而已
%结果
figure
plot(t,x)
xlabel('Time [s]')
ylabel('Magnitude')
setfontsize(14);
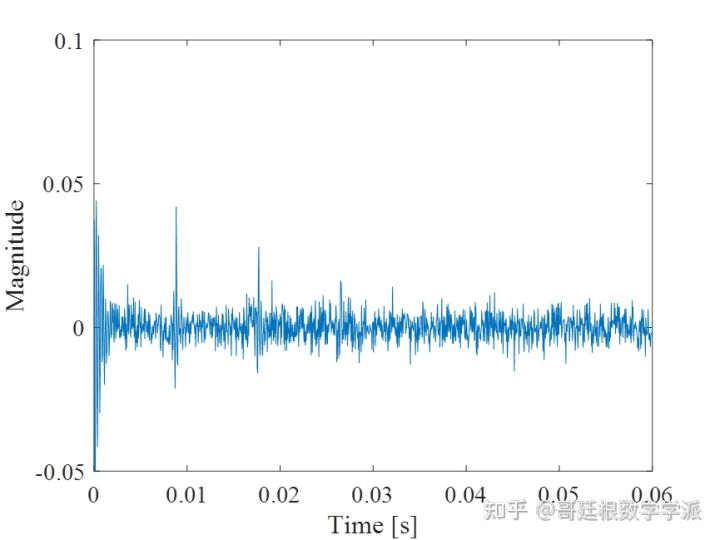
% Cepstrum
figure
plot(t,y)
xlabel('Time [s]')
ylabel('Magnitude')
setfontsize(14);
xlim([0 0.06])
ylim([-0.05 0.1])
同样以第3个轴承Z轴70Hz第8组外圈故障信号为例
fs = 10240;
t = 1/10240:1/10240:1;
x1 = load('#8');x1 = x1.Z;x1 = x1(1:5120*2);x1 = x1-mean(x1);
x=x1;
BPFI = 6.587;
v = 70;
N = length(x);
%倒谱滤波(变换)
y = real(ifft(log(abs(fft(x)))));
%结果
figure(1)
subplot(2,1,1)
plot(t,x)
xlabel('Time [s]')
ylabel('Magnitude')
setfontsize(14);
subplot(2,1,2)
plot(t,y)
xlabel('Time [s]')
ylabel('Magnitude')
setfontsize(14);
%包络谱
figure(2)
subplot(2,1,1)
[pEnvInner, fEnvInner, xEnvInner, tEnvInner] = envspectrum(x, fs);plot(fEnvInner, pEnvInner)
xlim([0 800]);ncomb = 20;helperPlotCombs(ncomb,BPFI*v);xlabel('Frequency(Hz)');ylabel('Ampitude')
subplot(2,1,2)
[pEnvInner, fEnvInner, xEnvInner, tEnvInner] = envspectrum(y, fs);plot(fEnvInner, pEnvInner)
xlim([0 800]);ncomb = 20;helperPlotCombs(ncomb,BPFI*v);xlabel('Frequency(Hz)');ylabel('Ampitude')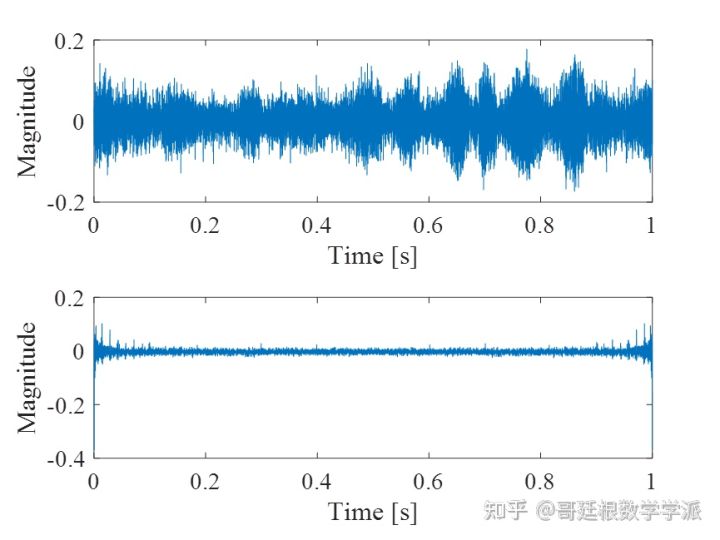
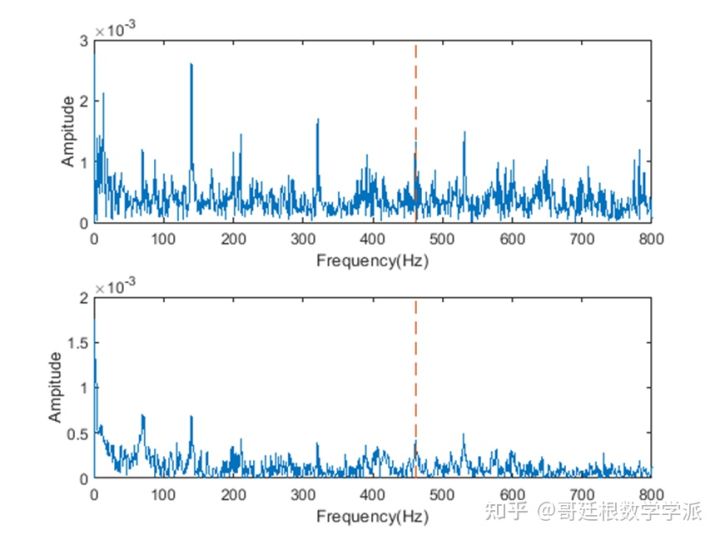
emmmmm
卡尔曼滤波
基于卡尔曼滤波的资料可就太多太多了,还是先上一个模拟信号
fs = 1000;
t = 0:1/fs:5-1/fs;
% x1 为信号加噪声
x1 = cos(2*pi*10*t)+0.2*randn(size(t));
noise = 0.2*randn(1,fs);
% 仿真信号x前1秒为噪声,后面为需要降噪的信号
x = [noise x1];
N = length(x);
t = 0:1/fs:(N-1)/fs;
%卡尔曼滤波降噪
[output varargout] = StandardKalmanFilter(x,0.5*fs,0.5*fs);
%结果
% Original waveform
figure
plot(t,x)
% De-noised signal
hold on
plot(t,output);
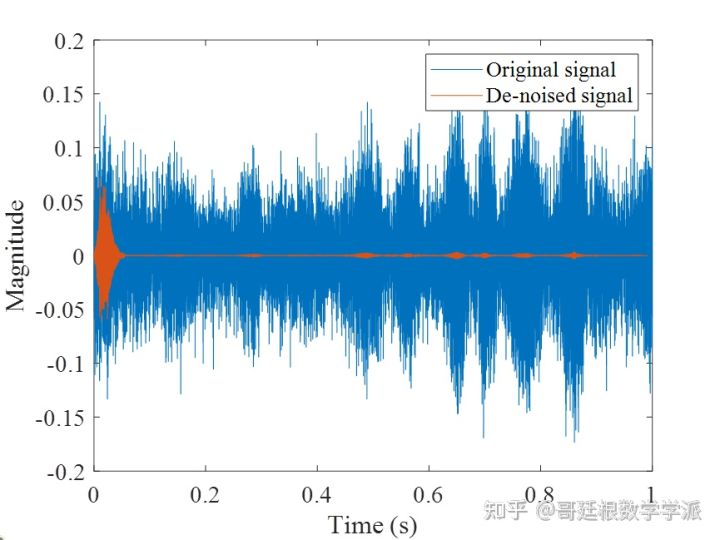
legend('Original signal','De-noised signal');
xlabel('Time (s)')
ylabel('Magnitude')
setfontsize(14);
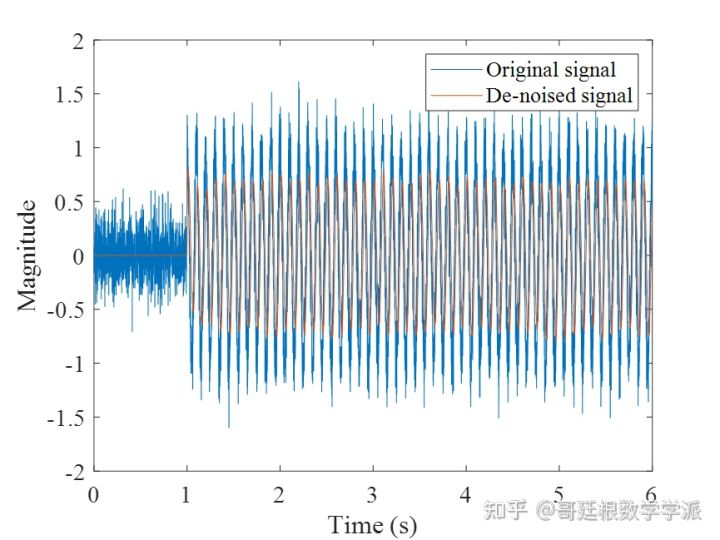
同样以第3个轴承Z轴70Hz第8组外圈故障信号为例
fs = 10240;
t = 1/10240:1/10240:1;
% x1 为信号加噪声
x1 = load('#8');x1 = x1.Z;x1 = x1(1:5120*2);x1 = x1-mean(x1);x1=x1';
noise = 0.2*randn(1,fs);
% 仿真信号x前1秒为噪声,后面为需要降噪的信号
x = [noise x1];
N = length(x);
%卡尔曼滤波降噪
[output varargout] = StandardKalmanFilter(x,0.5*fs,0.5*fs);
%结果
% Original waveform
figure
t = 0:1/fs:(N-1)/fs;
plot(t,x)
% De-noised signal
hold on
plot(t,output);
legend('Original signal','De-noised signal');
xlabel('Time (s)')
ylabel('Magnitude')
setfontsize(14);
BPFI = 6.587;
v = 70;
[pEnvInner, fEnvInner, xEnvInner, tEnvInner] = envspectrum(x, fs);plot(fEnvInner, pEnvInner)
xlim([0 800]);ncomb = 20;helperPlotCombs(ncomb,BPFI*v);xlabel('Frequency(Hz)');ylabel('Ampitude')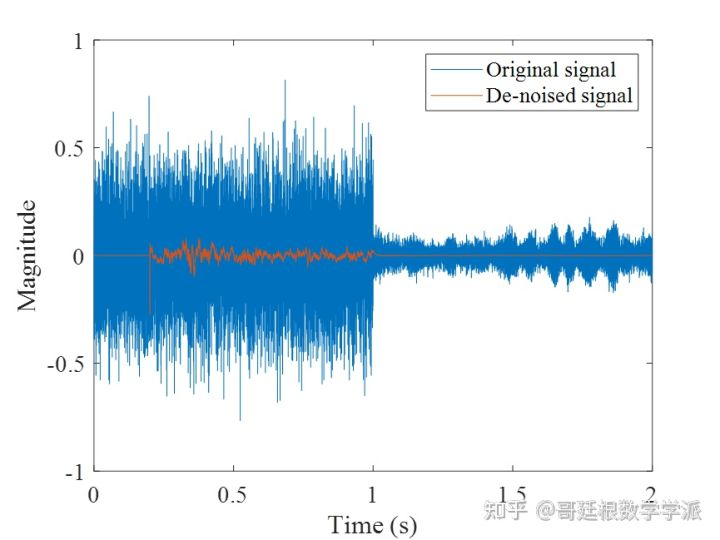
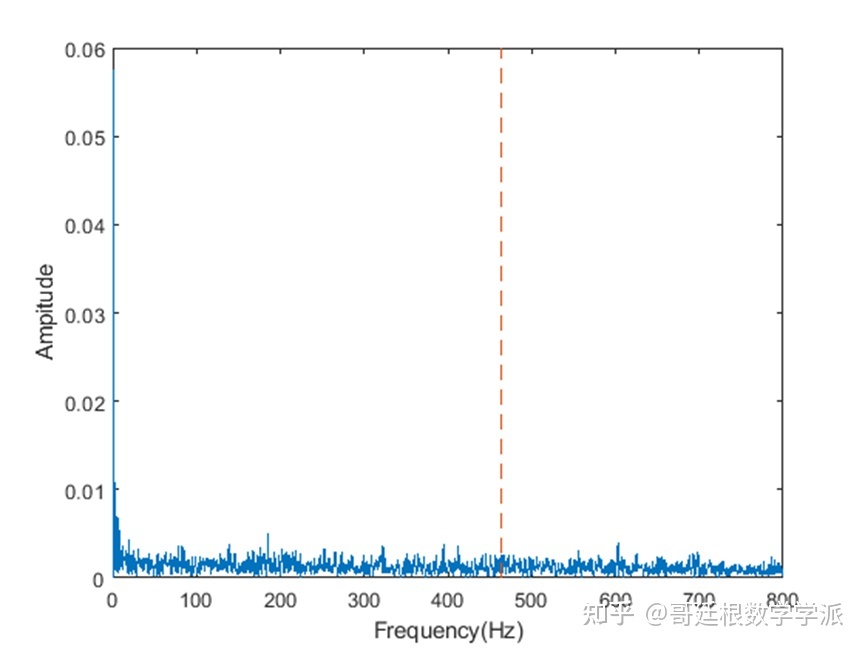
滑动平均滤波
以模拟信号为例
fs = 1000;
t = 0:1/fs:1-1/fs;
x = cos(2*pi*10*t)+0.2*randn(size(t));
x = x';
N = length(x);
%移动平均
windowlength = 10;
output = movingmean(x,windowlength,[],[]);
%结果
% Original waveform
figure
plot(t,x)
% De-noised signal
hold on
plot(t,output)
xlabel('Time [s]')
ylabel('Magnitude')
legend('Original signal','De-noised signal');
setfontsize(14);
同样以第3个轴承Z轴70Hz第8组外圈故障信号为例,窗口长度首先设置为100
fs = 10240;
t = 0:1/fs:1-1/fs;
x1 = load('#8');x1 = x1.Z;x1 = x1(1:5120*2);x1 = x1-mean(x1);
x = x1;
N = length(x);
%移动平均
windowlength =100;
output = movingmean(x,windowlength,[],[]);
%结果
% Original waveform
figure
plot(t,x)
% De-noised signal
hold on
plot(t,output)
xlabel('Time [s]')
ylabel('Magnitude')
legend('Original signal','De-noised signal');
setfontsize(14);
figure(2)
BPFI = 6.587;
v= 70;
subplot(2,1,1)
[pEnvInner, fEnvInner, xEnvInner, tEnvInner] = envspectrum(x, fs);plot(fEnvInner, pEnvInner)
xlim([0 800]);ncomb = 20;helperPlotCombs(ncomb,BPFI*v);xlabel('Frequency(Hz)');ylabel('Ampitude')
subplot(2,1,2)
[pEnvInner, fEnvInner, xEnvInner, tEnvInner] = envspectrum(output, fs);plot(fEnvInner, pEnvInner)
xlim([0 800]);ncomb = 20;helperPlotCombs(ncomb,BPFI*v);xlabel('Frequency(Hz)');ylabel('Ampitude')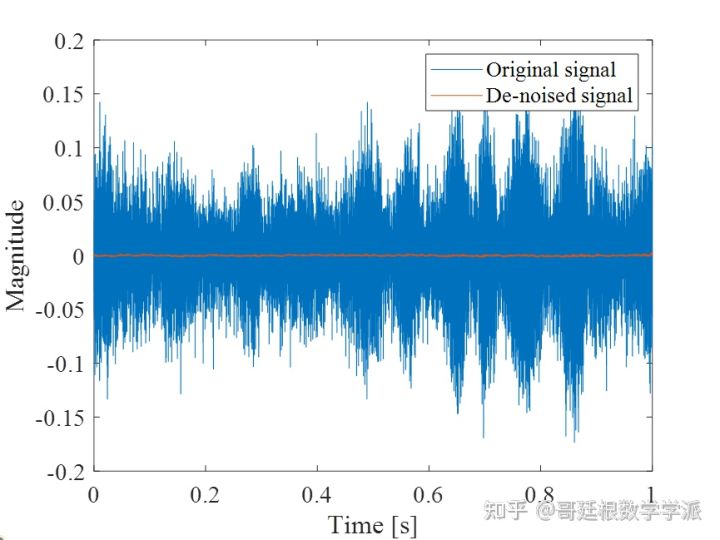
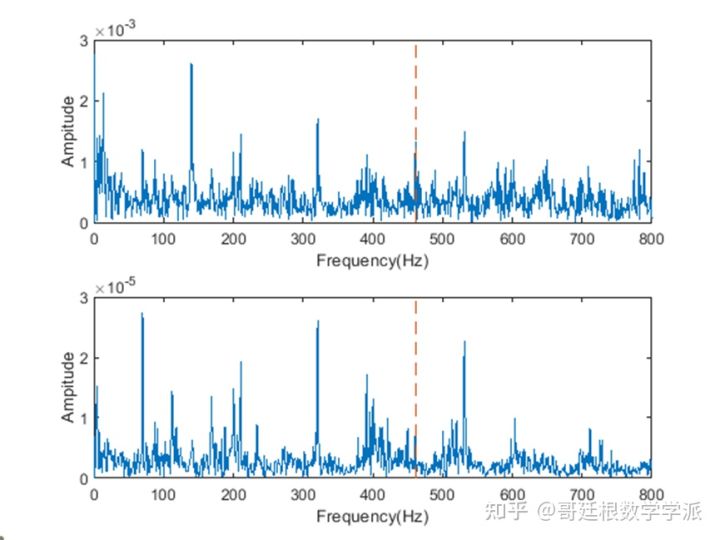
窗口长度设置为200

窗口长度设置为300
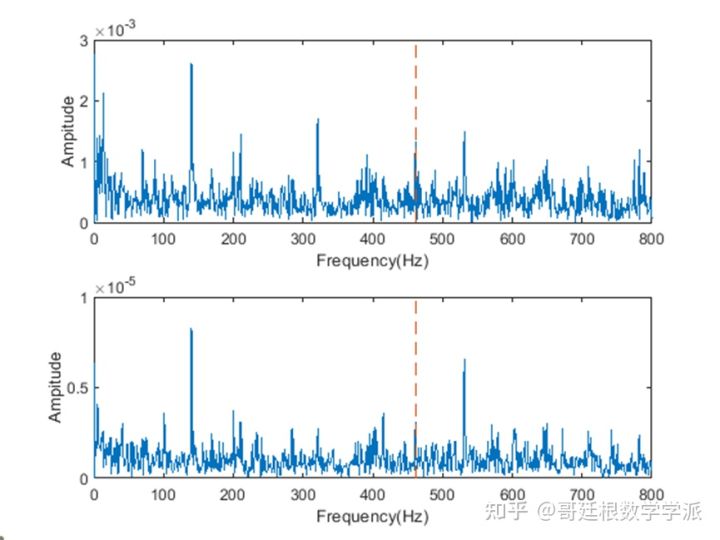
功率谱
关于功率谱密度,可参考如下文章
功率谱密度如何理解? - 張無忌的回答 - 知乎 https://www.zhihu.com/question/29520851/answer/241700599
仍以第3个轴承Z轴70Hz第8组外圈故障信号为例
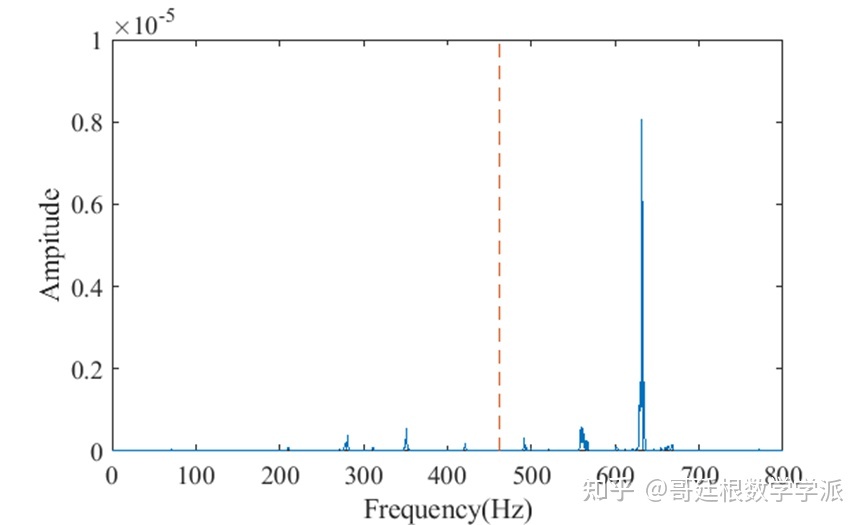
维纳滤波
关于维纳滤波,请参考如下文章
信号处理--维纳滤波(wiener filter) - 一支稳定的箭的文章 - 知乎 https://zhuanlan.zhihu.com/p/420474730
首先仍以一个模拟信号为例
fs = 1000;
t = 0:1/fs:5-1/fs;
% x1 为信号加噪声
x1 = cos(2*pi*10*t)+0.2*randn(size(t));
noise = 0.2*randn(1,fs);
% 仿真信号x前1秒为噪声,后面为需要降噪的信号
x = [noise x1];
N = length(x);
t = 0:1/fs:(N-1)/fs;
%维纳滤波
output=WienerScalart96(x,fs,0.5);
%结果
% Original waveform
figure
plot(t,x)
% De-noised signal
hold on
plot(0:1/fs:(length(output)-1)/fs,output)
legend('Original signal','De-noised signal');
xlabel('Time (s)')
ylabel('Magnitude')
setfontsize(14);
然后以第3个轴承Z轴70Hz第8组外圈故障信号为例
fs = 10240;
t = 0:1/fs:1-1/fs;
x1 = load('#8');x1 = x1.Z;x1 = x1(1:5120*2);x1 = x1-mean(x1);
x = x1;
N = length(x);
output=WienerScalart96(x,fs,0.4);
%结果
figure
plot(t,x)
% De-noised signal
hold on
plot(0:1/fs:(length(output)-1)/fs,output)
legend('Original signal','De-noised signal');
xlabel('Time (s)')
ylabel('Magnitude')
setfontsize(14);
figure
BPFI = 6.587;
v = 70;
subplot(2,1,1)
[pEnvInner, fEnvInner, xEnvInner, tEnvInner] = envspectrum(x, fs);plot(fEnvInner, pEnvInner)
xlim([0 800]);ncomb = 20;helperPlotCombs(ncomb,BPFI*v);xlabel('Frequency(Hz)');ylabel('Ampitude')
subplot(2,1,2)
[pEnvInner, fEnvInner, xEnvInner, tEnvInner] = envspectrum(output, fs);plot(fEnvInner, pEnvInner)
xlim([0 800]);ncomb = 20;helperPlotCombs(ncomb,BPFI*v);xlabel('Frequency(Hz)');ylabel('Ampitude')