优先队列及使用场景

普通的队列是一种先进先出的数据结构，元素在队列尾追加，而从队列头删除。在优先队列中，元素被赋予优先级。当访问元素时，具有最高优先级的元素最先删除。优先队列具有最高级先出 (first in, largest out)的行为特征。通常采用堆数据结构来实现。

优先队列有最大优先队列和最小优先队列，分别由最大堆和最小堆实现。其中，最大优先队列可用于如共享计算机系统的作业调度，当一个作业完成或中断，则获取优先级最高的作业执行；最小优先队列可用于基于时间驱动的模拟器，每一个节点代表一个时间，key就是时间，事件的执行按照时间顺序模拟。

最大优先队列

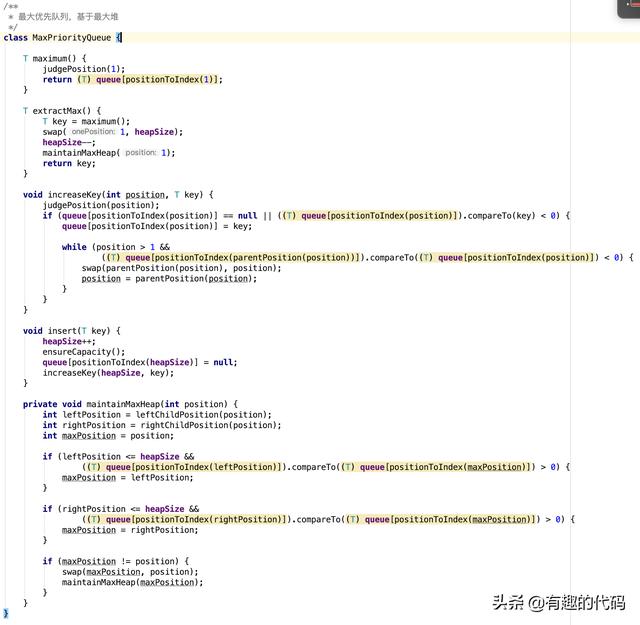
方法时间复杂度分析：

1、maximum：通过索引获取最大堆位置为1的元素。因此，时间复杂度是常量O(1)。

2、extractMax：获取并删除最大堆位置为1的元素。最后一个元素和第一个元素交换，导致第一个元素可能不符合最大堆，调整的过程最多为堆的高度。因此，时间复杂度是O(lgn)。

3、increaseKey：将指定位置用key替换，其中key必须大于原替换值。因为key大于原替换值，所以以key为根的子树符合最大堆，而key做为子节点可能会违反最大堆，需要逐级向上确认是否符合最大堆规范，若不符合，则key需要和其父节点交换。直到root节点为止。调整的过程最多为堆的高度。因此，时间复杂度是O(lgn)。

4、insert：插入元素key。调整堆长度增一，调用increaseKey在堆尾用key替换。因此，时间复杂度是O(lgn)。

总结：

在n个元素的优先队列中，所有操作都可以在O(lgn)时间内完成。

最小优先队列

方法时间复杂度同最大优先队列。