粗糙集算法集合（代码未整合版）

# To add a new cell, type '# %%'
# To add a new markdown cell, type '# %% [markdown]'
# %%
import numpy as np
import numexpr as ne

# %% [markdown]
# 粗糙集是波兰理工大学Z.pawlak教授提出用来研究不完整数据，不精确知识的表达、学习，归纳等的一套理论
# 
# 它是一种新的处理模糊和不确定性问题的数学工具，已被广泛应用于知识发现、机器学习、决策支持、模式识别、专家系统及归纳推理等领域。
# 
# 粗糙集理论的特点是能够分析隐藏在数据中的事实，又不需要关于数据附加信息。
# 
# 其主要思想是在保持分类能力不变的前提下，通过知识约简，导出问题的决策或分类规则。
# 

# %%
data = np.array([
        ["病人","头疼","肌肉疼","体温","流感"]
        ,["e1",'是', '是', '正常', '否']
        ,["e2",'是', '是', '高', '是']
        ,["e3",'是', '是', '很高', '是']
        ,["e4",'否', '是', '正常', '否']
        ,["e5",'否', '否', '高', '否']
        ,["e6",'否', '是', '很高', '是']])


# %%
data

# %% [markdown]
# # 決策屬性

# %%
def decision_factor(info):
    return info[1:,-1]
decision_factor(data)


# %%
def split_decision_factor(info):
    dec_fac = decision_factor(info)
    return {i:((dec_fac==i).dot(np.ones(dec_fac.shape[0])),set(info[1:,0][np.ravel(np.argwhere(dec_fac==i))]),dec_fac==i) for i in np.unique(dec_fac)}
split_decision_factor(data)

# %% [markdown]
# # 论域

def universe_of_discourse(info):
    return info[1:,:]
# %%
universe_of_discourse(data)

# %%
# 条件集
def attribute_set(info):
    return info[1:,1:-1]

attribute_set(data)


# %%
def getX(info,*keyword):
    return np.array([info[:,np.argwhere(info[0] == key)[0][0]] for key in np.array(keyword)]).T

getX(data,"头疼","肌肉疼")

# %% [markdown]
# # 求出等价商集

# %%
def quotient_set(info,*keyword):
    knowledge = getX(info,*keyword)
    univ_disc = universe_of_discourse(knowledge)
    e = info[1:,0]
    result = {}
    for keys in {tuple(i) for i  in univ_disc}:
        _index = np.ravel(np.argwhere((univ_disc==np.array(keys)).dot(np.ones(len(keyword)))==len(keyword)))
        e_index = e[_index]
        result.update({tuple(e_index):univ_disc[_index]})
    return result

quotient_set(data,"头疼","肌肉疼")

# %%
def equivalence_class(C,R,A):
    column = np.ravel([np.argwhere(A[0]==c) for c in C])
    change_U = A.T[column].T
    univ_disc = universe_of_discourse(change_U)
    Rm = len(R)
    arr_one = np.ones(Rm)
    e = A[1:,0]
    return e[(univ_disc==R).dot(arr_one)==Rm]

equivalence_class(C =["头疼","肌肉疼"],R=['否', '是'],A = data)

import math
from itertools import product

def combinationL(loop_val): # 多list组合函数
    return np.array([i for i in product(*loop_val)])

def drop_dim(List):
    return [j for i in List for j in i]

def comparefunc(A,B,bi,e,D,cname):
    result = dict()
    m,n = A.shape
    t = -1
    for a in A:
        t+=1
        for b in B:
            bn = b.shape[0]
            if bn < n:
                for i in range(math.ceil(n/bn)):
                    temp1 = (a[i:i+bn]==b).all()  
                    if temp1:
                        index_str = (e[t],i,i+bn)
                        key = "{}{}".format(e[bi[t]],index_str)
                        result1 = {key:{"决策属性":D[bi[t]],"论域":e[bi[t]],"条件属性":a,"等价关系":b,"元素段坐标":index_str}}    
                        result.update(result1)
            else:
                temp2 = (a==b).all()
                if temp2:
                    index_str = (e[t],0,bn)
                    key = "{}{}".format(e[bi[t]],index_str)
                    result2 = {key:{"决策属性":D[bi[t]],"论域":e[bi[t]],"条件属性":a,"等价关系":b,"元素段坐标":index_str}}
                    result.update(result2)
    return result

def creater_equivalence_relation(S,C):
    cname = C
    e = S[1:,0] # 论域
    D = S[1:,-1] # 决策属性
    Ddistion = set(D)
    columns = np.ravel([np.argwhere(S[0]==c) for c in C]) #选择列
    C = S.T[columns].T[1:] #选择的条件属性集
    Cname = S.T[columns].T[0]
    Cm ,Cn = C.shape
    Dbool_index = {d:np.ravel(np.argwhere(D==d)) for d in Ddistion } # 决策属性分类
    Cclass =[]
    for ci,bi in Dbool_index.items():
        Cb = C[bi]
        cdistion = [set(Cb[:,c]) for c in range(len(Cb[0]))]
        for i in range(len(cdistion)):
            ccomb = combinationL(cdistion[:i+1])
            temp_c = comparefunc(C[bi],ccomb,bi,e,D,cname)
            Cclass.append(temp_c)
    return Cclass


def equivalence_relation(S,C,keyword=None):
    D = S[1:,-1] # 决策属性
    def filter_(ds):
        result_e , result_R ,result_D ,result_location = [],[],[],[]
        data = creater_equivalence_relation(ds,C)
        for i in data:
            for ik,iv in i.items():
                e = iv['论域']
                R = iv['等价关系']
                D = iv['决策属性']
                location = iv['元素段坐标']
                result_e.append(e)
                result_R.append(R)
                result_D.append(D)
                result_location.append(C[location[-2]:location[-1]])
        def clear(List):
            bool_func = np.array([np.ravel(np.argwhere(np.array(result_e) == coder)) for coder in set(result_e)])
            eq_  = np.array(List)[bool_func]
            return dict(enumerate(eq_))
        return {'论域':clear(result_e),'等价关系':clear(result_R),'决策属性':clear(result_D),'元素段坐标':clear(result_location)}
    if keyword == "splitD":
        Ddistion = set(D)
        DS = {d:filter_(np.vstack((S[0],S[1:][D==d]))) for d in Ddistion}
        return DS
    elif keyword == None:
        return creater_equivalence_relation(S,C)
equivalence_relation(data,["头疼","肌肉疼",'体温'],keyword="splitD")



# %% [markdown]
# # 给定X
def definitionX(info,X,*keyword):
    knowledge = getX(info,*keyword)
    univ_disc = universe_of_discourse(knowledge)
    data_dict = {i:j for i,j in zip(info[1:,0],univ_disc)}
    return {X:np.array([data_dict[i] for i in X])} ,univ_disc

# %% [markdown]
# # 上/下近似/边界线

# %%
from itertools import combinations

def Rouh_set_all(info,X,*keyword,change_approx = 'lower'):
    quot_set = quotient_set(info,*keyword)
    X ,knowledga = definitionX(info,X,*keyword)
    intersect_list,index_list = [],[]
    for set_ in quot_set:
        intersect = (set(set_)&set(list(X)[0]))
        lenght = len(intersect)    
        if lenght > 0:
            intersect_list.append(set_)
            index_list.append(lenght)
    if change_approx == 'lower':
        return set(intersect_list[index_list.index(min(index_list))])
    elif change_approx == "upper":
        return {j for i in range(len(intersect_list)) for j in intersect_list[i]}
    elif change_approx == "boundary_region":
        upper = set([j for i in range(len(intersect_list)) for j in intersect_list[i]])
        lower = set(list(intersect_list[index_list.index(min(index_list))]))
        return upper-lower
    elif change_approx=="positive_field":
        return set(list(intersect_list[index_list.index(min(index_list))]))
    elif change_approx == "negative_field":
        univ_disc = set(info[1:,0])
        return univ_disc-set(intersect_list[index_list.index(min(index_list))])
    elif change_approx == "R_exact_sets":
        temp = [list(combinations(intersect_list,i)) for i in range(1,len(intersect_list))]
        exact = [e for e in drop_dim(temp) if set(len(e)==1 and e[0] or drop_dim(e))==set(X)]
        lenght_set = len(exact)
        return lenght_set > 0 and {"R exact sets":exact} or "Rouh set" 

# %% [markdown]
# # 下近似

# %%
def lower_approximation(info,X,keyword):
    return Rouh_set_all(info,X,*keyword,change_approx = 'lower')

lower_approximation(data,("e2","e3","e5"),("头疼","肌肉疼"))

# %% [markdown]
# # 上近似

# %%
def upper_approximation(info,X,keyword):
    return Rouh_set_all(info,X,*keyword,change_approx = 'upper')
upper_approximation(data,("e2","e3","e5"),("头疼","肌肉疼"))

# %% [markdown]
# # 边界线

# %%
def boundary_region(info,X,keyword):
    return Rouh_set_all(info,X,*keyword,change_approx = 'boundary_region')

boundary_region(data,("e2","e3","e5"),("头疼","肌肉疼"))

# %% [markdown]
# # 正域

# %%
def positive_field(info,X,keyword):
    return Rouh_set_all(info,X,*keyword,change_approx = 'positive_field')
positive_field(data,("e2","e3","e5"),("头疼","肌肉疼"))

# %% [markdown]
# # 负域

# %%
def negative_field(info,X,keyword):
    return Rouh_set_all(info,X,*keyword,change_approx = 'negative_field')
negative_field(data,("e2","e3","e5"),("头疼","肌肉疼"))

# %% [markdown]
# # 精确集

# %%
def R_exact_sets(info,X,keyword):
    test = Rouh_set_all(info,X,*keyword,change_approx = 'R_exact_sets')
    return test != 'Rouh set' and test or "this relationship has no R exact set"
R_exact_sets(data,("e2","e3","e5"),("头疼","肌肉疼"))

# %% [markdown]
# # 检验给定X是否是论域的粗糙集

# %%
def rouh_set(info,X,keyword):
    return Rouh_set_all(info,X,*keyword,change_approx = 'R_exact_sets') == 'Rouh set'
rouh_set(data,("e2","e3","e5"),("头疼","肌肉疼"))

# %% [markdown]
# # 近似分类的:精度/粗糙度/质量

# %%
# 近似分类
def approximate_classification(info,Uname,changeD):
    U , n = info.shape
    Dinfo = {d:np.vstack((info[0],info[1:][info[1:,-1]==d])) for d in set(info[1:,-1])}
    new_info = Dinfo[changeD]
    e = tuple(new_info[1:,0])
    if rouh_set(info,e,Uname):
        lowerR = lower_approximation(info,e,Uname)
        pperR = upper_approximation(info,e,Uname)
        boundaryR = boundary_region(info,e,Uname)
        positiveR = positive_field(info,e,Uname)
        negativeR = negative_field(info,e,Uname)
        alphaR = len(lowerR)/len(pperR)
        rhoR = 1- alphaR
        gammaR = len(lowerR)/U
        return {"近似分类精度":alphaR,"粗糙度":rhoR,"近似分类质量":gammaR,"上近似":pperR,"下近似":lowerR,"决策边界":boundaryR,"正域":positiveR,"负域":negativeR}
    else:
        test = Rouh_set_all(info,e,*Uname,change_approx = 'R_exact_sets')
        return test
approximate_classification(data,('头疼', '肌肉疼', '体温'),"是")

# 知识约简
from itertools import permutations,combinations
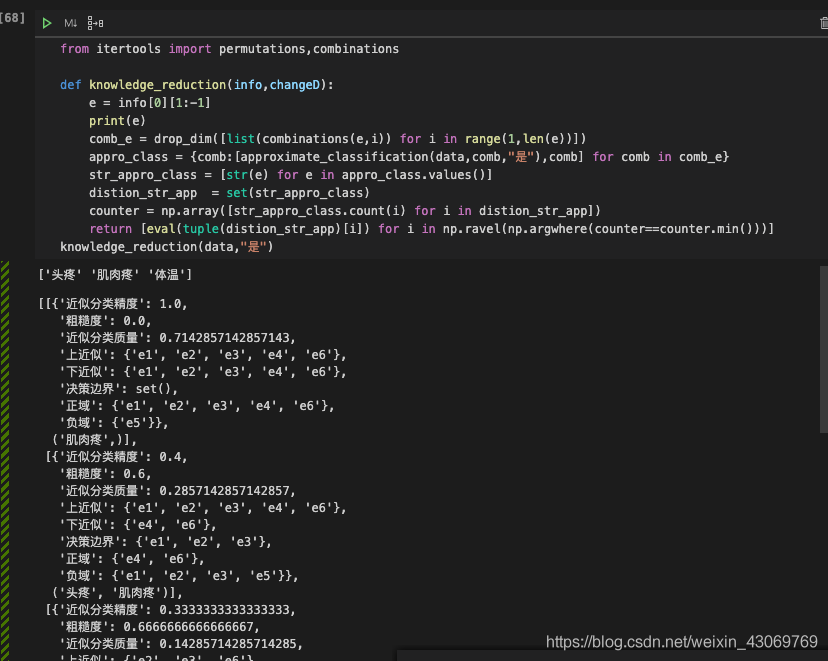
def knowledge_reduction(info,changeD):
    e = info[0][1:-1]
    print(e)
    comb_e = drop_dim([list(combinations(e,i)) for i in range(1,len(e))])
    appro_class = {comb:[approximate_classification(data,comb,"是"),comb] for comb in comb_e}
    str_appro_class = [str(e) for e in appro_class.values()]
    distion_str_app  = set(str_appro_class)
    counter = np.array([str_appro_class.count(i) for i in distion_str_app])
    return [eval(tuple(distion_str_app)[i]) for i in np.ravel(np.argwhere(counter==counter.min()))]#,appro_class
knowledge_reduction(data,"是")