vc++获取的蓝牙设备信息中rssi的值_RSSI 滤波算法在室内定位技术上的应用


概述

随着物联网时代的到来，低功耗室内定位越来越收到广大群众的青睐。本文针对蓝牙 BLE 和ZigBee 技术在室内定位上的应用，通过对蓝牙和 ZigBee 无线传播路径损耗的分析，得出一种基于 RSSI(Received Signal Strength Indicator，信号强度指示)的节点定位算法中的提高 RSSI 精度的各种滤波理论分析。

关键词：蓝牙BLE；ZigBee；室内定位；RSSI，滤波

目前，无线传感器网络领域提出了很多定位算法，可根据其定位类型分为测距定位算法和无测距定位算法。本文主要研究以RSSI 为定位信息的测距定位算法，RSSI 测距定位算法具容易实现，开发成本低，安装快捷方便等优点。其中，蓝牙BLE 技术和ZigBee 技术在无线低功耗室内精准定位应用中脱颖而出。

提高RSSI 精度的滤波算法

均值滤波

取每个一个节点的多个 RSSI 值，求得算术平均值，作为测试结果。

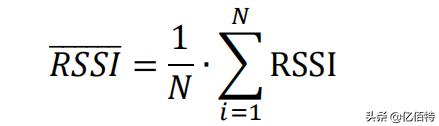
e7ac3d0ffc699381ecd36084c43a121a.png

优点：该方法简单，容易实现，样本容量N 越大，精度越高。

缺点：RSSI 受干扰比较大时，其波动比较大，导致精度降低。

递推平均滤波

把连续收到的N 个RSSI 看成一队列，队列长度固定为N，每收到一个新RSSI 值后放于对尾，扔掉原来队首RSSI 值，把队列中N 个RSSI 取算术平均值，作为测试结果。

优点：对周期性干扰抑制能力强。

缺点：不合适脉冲性干扰和随机性干扰大的场合。

中值滤波

在采集N(N 为奇数)个RSSI 值之后，将这 N 个RSSI 值按大小顺序排列，取其正中间的 RSSI 值作为滤波输出。

RSSI = Med{1 + 2 + ⋯ + }

优点：对偶然性干扰有良好的抑制效果。

缺点：容量不多，脉冲干扰较强的情况下该滤波效果不理想。

狄克逊检验法滤波

是通过极差比判定和剔除异 常数据。该方法认为异常数据应该是最大数据和最小数据，因此该方法是将数据按大小排列，检验最大数据和最小数据是否是异常数据。以样本容量小于等于 30 为例，具体步骤如下：

  • 将对同一节点多次测量到的 RSSI 值按从小到大的顺序排列，{RSSI(1),RSSI(2),RSSI(3),⋯,RSSI(n-2), RSSI(n-1),RSSI(n)}，并确定检出水平α=0.05。
  • 根据狄克逊统计公式，有

当 n=3~7 时检验高端异常值：

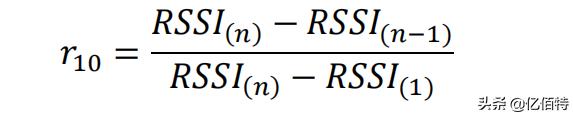
3f83f460143bd9fc296a80d982be7b67.png

检验低端异常值：

当 n=8~10 时检验高端异常值：

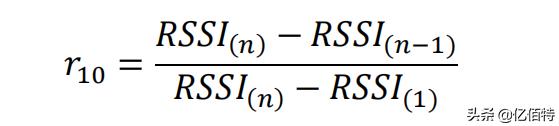
7f8228f124c41989e78205737be65f8b.png

检验低端异常值：

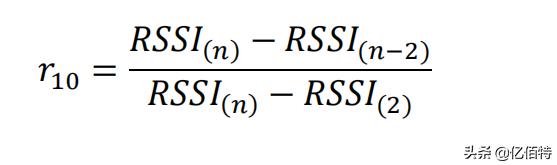
856a7362ecacecdcb6c3efe7d6386113.png

检验低端异常值：

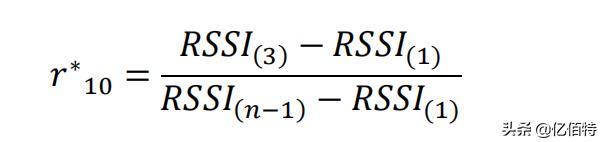
124ee1fe5b894403ae42e68723f4b320.png

当 n=14~30 时检验高端异常值：

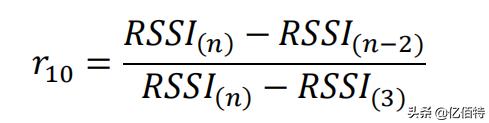
82c2983ab6c6268fd7511467f8155327.png

检验低端异常值：

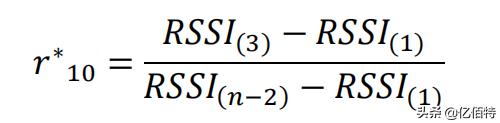
9606dd7a6bbefb450a2fb06359b46fe3.png

(3)根据检出水平α，查狄克逊检验的临界值表，在狄克逊检验法的临界值表中查出对应α，n 的临界值 D(α,n)

(4)当 ∗，且﹥D(α,n)时，RSSI(n)为异常 值；当∗﹥ ，且∗﹥D(α,n)时，RSSI(1)为异常值；否则判断未发现异常值。

(5)去除异常值后，对剩下的样本数据，重复执行步骤(1)~步骤(5)，直到不再检出异常值为止。最后剩下的数据可求其算数平均值作为最后滤波输出。优点：狄克逊检验法能够有效地去除样本中的异常值缺点：此算法需要查表，通常与其他的滤波算法混合滤波，复杂度较高

高斯滤波

对同一个节点接收到的多个 RSSI 值中，由于各种干扰，必然存在由误差引起的小概率事件，通过高斯模型选取高概率发生区的 RSSI 值作为有效值，再求其几何平均值，这种方法能够有效地减少小概率、大干扰对整体测量数据的影响，提高定位的准确性。

RSSI 服从 (0,σ2)的高斯分布，其概率密度函数为：

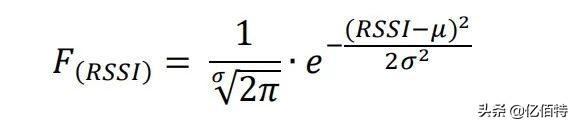
8d4a067cd63233ee819aa9ccba0eccc9.png

其中：

区间(μ − σ ≤ () < + )的概率为：

P(μ − σ ≤ < μ + σ) = ( + ) − ( + ) = ∅(1) − ∅(−1) = 2∅(1) − 1 = 06826

该区间为高概率发生区，选择高斯函数值在该区间的对应的 RSSI 值，再将这些 RSSI 值做算术平均作为滤 波优化的 RSSI 值

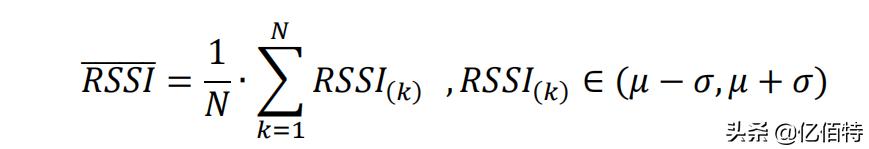
58380f675c01bde7a6df708ca4f60777.png

优点：高斯滤波解决了 RSSI 在实际中易受干扰，稳定性差的问题，以提高定位精度。缺点：对阴影效果、能量反应等长时间干扰问题处理效果差。

速度常量滤波

基于物体在一定范围内的移动并不是任意的，当前位置和前一时刻的位置存在一种相互关系的思想，采用速度常量，使移动点保持匀速运动。

估算值：

预测值：

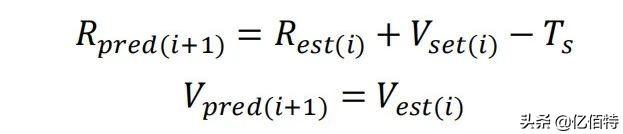
5716bf419cfc8417a9fb9d52a18de7a8.png

式中: ()为 i 时刻信号强度的测量值；()为 i 时刻信号强度的预测值；()为 i 时刻信号强度滤波值；()为 i 时刻信号强度变化率的滤波值；(+1)为 i 时刻信号强度变化率的预测值；a,b 为增益常量；为采样时间间隔。优点：基于速度常量的滤波算法能够有效地减小信号波动给测量带来的影响

卡尔曼滤波

卡尔曼滤波的基本思想是：以最小均方误差为最佳估计准则，采用信号与噪声的状态空间模型，利用前一时刻的估计值和当前时刻的观测值来更新对状态变量的估计，求出当前时刻的估计值，算法根据建立的系统方程和观测方程对需要处理的信号做出满足最小均方误差的估计。

RSSI 用表示，采样过程的数学模型可以表示为 一个高斯白噪声序列驱动的一阶自递推过程，其状态方程和观测方程可表示为：

状态方程：

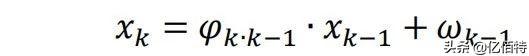
45e2733f5e2276f974870e673db1eabe.png

观测方程：

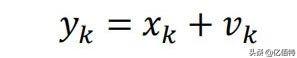
ce36cb1fd05650076360842f0dae7600.png

式中：为 k 时刻的 RSSI 值；为 k 时刻对进行测量得到的观测值；−1和(k∈N)都是独立同分布的噪 声序列；−1表示驱动变化的高斯白噪声序列；表示 k 时刻测量过程所引入的噪声，过程激励噪声协方差矩阵为 Q，观测噪声协方差矩阵为 R，其中：

联立状态式和观测方程式，算法实现流程为：

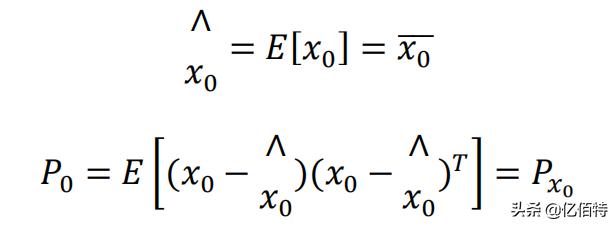
3d3b50b9e20cd2ab10112e3a66214493.png

时间更新方程：

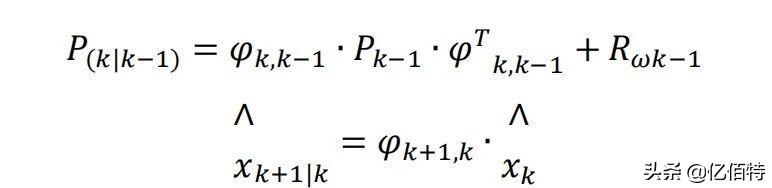
256703745847e5ac106781123fb919d2.png

测量更新方程：

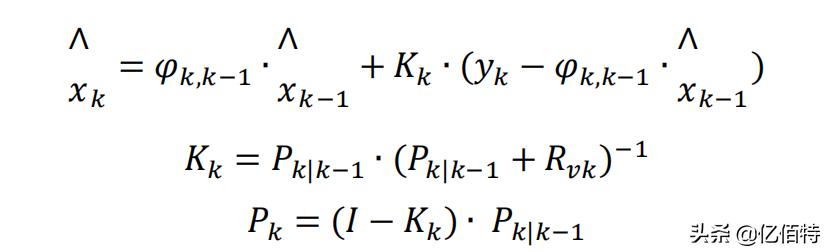
2dde9a6e31ed179224411a9b1af8bf89.png

式中：|−1为一步预测均方误差阵；∧−1|为状态一步预测值；∧为状态滤波值；为滤波增益矩阵；为滤波均方误差阵。优点：卡尔曼滤波能在一定程度上削弱由于噪声叠加造成的 RSSI 观测值偏离，经过卡尔曼算法处理后的 RSSI 值，稳定性更好。卡尔曼在目标跟踪方面也能取得很好的效果。

总结

以上论述了几种常用的 RSSI 滤波处理方法、原理，各种算法都有各自的特点，没有哪一种是绝对最优的，比如均值滤波，其算法简单，易实现，但是精度不高，处理效果不佳，而高斯滤波处理效果好了很多，但是实现起来变得复杂一些，节点消耗更多能耗，同时占用了更多内存空间。实际应用中要根据具体情况，均衡各方面需求，选择合适的滤波方法，也可多种算法混合使用，以达到最佳的滤波效果。不论蓝牙 BLE 还是 ZigBee，都需要得到经过滤波后的精确度提高的 RSSI 值，加入多维几何算法中进行位置计算，从而已得到较为精确的位置信息。上述滤波理论均从网上收集整理，以便于蓝牙 BLE 还是ZigBee 技术更加广泛应用到室内定位。