[文章于2019年11月16日发表于公众号*荷兰高等心理统计联盟*,欢迎关注联盟,汲取心理学管理学研究方法学新视角]
I. What is p-value & why is it problematic?
P值的定义是“Given that the null hypothesis of no effect is true, the probability of events as, or more, extreme than the observed data.” 也就是在零假设(H0)为真的前提下,观察到与实际观测数据相同、或更极端事件发生的概率。
P值是由被称为现代统计学之父的英国遗传学家兼统计学家Ronald Fisher在19世纪30年代提出的,Fisher建议设置一个显著性水平(significance level)作为参照点去判断结果是否显著,亦即根据所得结果我们是否能拒绝零假设。他建议使用α = 0.05来判断结果是否显著,大约距离正态分布的均值两个标准差的水平。若p值很小,那么或则零假设为真、并且观察到与实际观测数据相同或甚至更极端事件发生的小概率发生了,亦或者零假设被拒绝,效果不为零。由此,p值小于0.05被视为确定实验结果有效性的一大标准,依照p值来决定拒绝或是无法拒绝零假设。因为这种假设检定建立在零假设的基础上,所以被称为「零假设显著性检验(Null Hypothesis Significance Testing, 简称NHST)」。
然而,越来越多的学者开始质疑统计显著性的概念以及Fisher的p值的局限性。以下列出了其经常被质疑的四点:
1. As, or more extreme: p值定义中的更极端事件如何定义?
淑女品茶是关于假设检验的一个著名例子。
Fisher一位女同事声称可以尝出一倍奶茶是先加的牛奶还是先加的茶。Fisher不信,就设计了一个简单的实验,给她六杯奶茶,其中三杯先加的奶三杯先加的茶,而女同事则要说出哪些先加的牛奶那些先加的茶。女同事的判断结果为RRRRRW (前五次判断正确, 最后一次错误),依照Fisher的定义,“As, or more extreme”事件包括六次中错误一次或者六次都判断正确,概率为(1/2)^6* (6+1) = 0.109。
贝叶斯的先驱者Harold Jeffreys对此提出了质疑-为什么是固定六次实验(fixed experiment)呢?J.B.S. Haldane提出了另一种实验方式,与其固定实验次数,他提出不断地实验直到第一次判断错误发生(sequential experiment)。基于这个观点,‘更极端事件’被定义为第一次错误发生在第六次尝试之后的事件,概率为(1/2)^6 +(1/2)^7 + (1/2)^8 + … = (1/2)^5 = 0.031。
那么究竟判断结果是否显著是应该基于固定次数的实验还是非固定次数实验呢?由于对显著性的判断会因 ‘更极端事件’的定义而变化,而这个界定到现在都没有完全达成共识,一些学者因而提出放弃‘更极端事件’的使用而放在‘所发生事件’的概率上,也因此有了贝叶斯学派。
2. P-hacking & researcher degree of freedom
Chris Chambers在《心理学七宗罪(The Seven Deadly Sins of Psychology)》一书中提到了心理学的其中一个问题在于身为研究者的自由度,而这也是造成很多实证研究结果无法被重复的原因之一。与零假设显著性检验相对应的α= .05 代表着第一类错误(假阳性结果),零假设为真却被错误拒绝。0.05的界定,使得.049和.051的p值代表了截然不同的解释。很大一部分研究者(也许也包括你)在看到边缘显著(marginal significant) 或是表现出显著趋势的结果后会利用研究者的自由度进行一些操弄,比如继续收更多的数据(也许等数据量大了以后结果就由不显著变为显著了)、对异常值进行一些特殊处理、比较各种不同的分析方法然后报告最‘漂亮’的p值等等。
这种很容易引起假阳性结果的p-hacking加重了实验的不可重复性,阻碍了科研的发展和可信度。过于着眼于统计显著性会让人忽略事实的本质才是更重要的。也因此有人说“what’s good for scientist isn’t what’s good for science itself”,但这些都是后话了。
3. Significance more easily suggests aneffect when none exists.
因为显著性水平通常比贝叶斯推断中零假设的后验概率来的小,Fisher的零假设显著性检验相比贝叶斯更容易拒绝零假设,亦即更容易做出效果存在的推断。Significance too easily suggests an effect when none exists (Lindley, 1993).
4. 贝叶斯学派会认为p值的一大问题在于统计显著性检定是基于零假设为真,却没有考虑基于备择假设为真前提下的事件发生概率。贝叶斯就是基于此建立的。
5.P值不太好理解。很多人把p值误以为P(H | data),亦即根据所观察到的数据,假设有多大可能为真。这与p值的定义完全相违,p的正确解读如前文所述是基于零假设为真的前提下观察到同等或者更极端事件的概率。很多学者对p值的这种错误解读,自带朴素的贝叶斯思想。贝叶斯哲学逻辑相比p值更为直观易懂。
II. NHSTvs. Bayesian approach: Why is Bayesian prevailing?
贝叶斯假设检定:
1. 聚焦在‘实际观测数据’ & 同时考虑H0和H1的支持证据
Jeffreys (1961,p.385)说,“What the use of P implies, therefore, is that a hypothesis that may be true may be rejected because it has not predicted observable results that have not occurred.”,寓意p值依赖于零假设以及基于‘相同或更极端’事件的发生概率。Fisher的p值检验了在零假设成立的前提下与实际观测数据相同或更极端事件发生的概率。
贝叶斯因子(Bayes factor)与其不同的是,将重点放在实际观测数据上,比较了在各个假设成立的前提下观察到实际观测数据的概率,并且用比率来反映各个假设(比如零假设和备择假设)的相对可能性。其所反映的是一个比较的概念—比较分别基于零假设和备择假设得到观测数据的概率,因此在解释上比p值更为直观。
量化了备择假设H1和零假设H0的相对证据,亦即比较了在H1成立的前提下观察到观测数据的概率和在H0成立的前提下观察到数据的概率。 代表了观测数据在备择假设下的概率是在零假设下的10倍。代表观测数据更为支持H1,代表观测数据更为支持H0,贝叶斯因子由此作为知识更新因子(knowledge update factor)去修正先验信念(priorbeliefs),形成后验信念(posterior beliefs)。

2.考虑先验知识
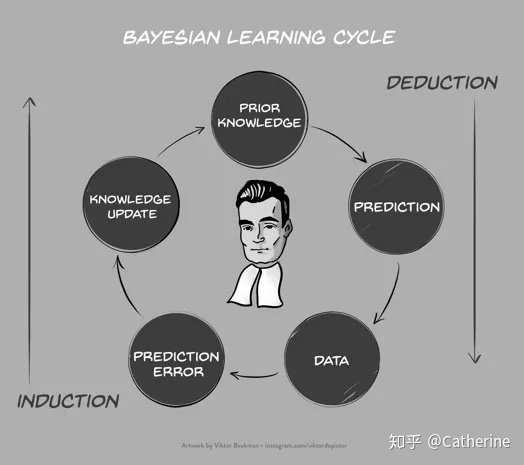
贝叶斯推断除了考虑观测数据在各个假设前提下的发生概率之外,还把先验知识纳入考量。从先验知识——到预测——再到观测数据构成了 ‘演绎(Deduction)’路径,而预测错误——更新知识——调整形成后验知识又构成了‘归纳(Induction)’路径,如此得到的后验知识又会成为之后研究的先验知识(“Today’s posterior belief becomes tomorrow’s prior”)、进而形成新的先验假设,由此形成「贝叶斯学习循环(Bayesian learning cycle)」。
先验知识在纳入考虑的过程中可以调整其先验分布的分散程度,以此来反映先验假设的强烈程度。比如可以选择默认先验(default prior),通常是较为离散的分布, 如此后验分布就更为取决于观测数据;亦可根据所研究问题前人的研究结果建立更为有根据的先验分布(informed prior distribution),通常分布更为集中,代表更强烈的先验假设,如此后验分布也就较少受本次观测数据的影响。
3. 对抽样计划没有要求& 实时监控证据强度的变化
贝叶斯假设检定不要求预先确定抽样方案及样本数。事实上,贝叶斯推断的序列分析(sequential analysis)可以实时监测贝叶斯因子的强度变化。依照Lee &Wagenmakers (2013)基于Jeffreys (1961)所修改的证据强度分类标准,贝叶斯因子值依照1-3, 3-10, 10-30,30-100, 100+可以归为支持H1(或H0)的较弱证据(anecdotal evidence)、中等证据(moderate evidence)、较强证据(strong evidence)、强力证据(very strongevidence)和极强证据(extreme evidence)。序列分析展现了贝叶斯因子亦即证据强度随样本量流入而变化。因此实验者可以考虑在贝叶斯因子达到一定数值(即数据明确支持其中一个假设)时停止继续收数据,而无需事先决定样本数,如此可以减少继续收更多数据带来的资源浪费。
III.Will Bayesian reference replace p-value in the future?
贝叶斯推论是如此的盛行,尤其现如今可重复性危机更加加剧了对传统p值显著性检定的质疑。那么p值是否会被贝叶斯统计检定所取代呢?
我个人的看法是,两者反映了完全不同的逻辑,一个基于H0为真而考虑同等或更极端的事件发生概率,一个聚焦在实验观测数据在各个不同假设下的相对概率。由此而言,贝叶斯因子与其说是p值的替代品(alternative),不如说是互补品(addition),相辅相成,让研究结果的翻译更加精准、容易理解。如上述所提,贝叶斯因子的优势,包括但不限于同时考虑不同假设、只聚焦在实际观测数值、逻辑与解释都较为直观、可以把前人研究结果作为先验知识纳入考量、没有抽样要求等等,可以补足p值的某些缺陷。
贝叶斯学派看似十分有前景,然而其依旧存在一些问题,此处列出以下三点:
1. 如果使用了十分强烈、有倾向性的先验分布,那么后验分布会很大程度上取决于先验分布,而较少受实际观测数据的影响,尤其是在观测数据的样本量较为小的情况下;若是使用默认的没有倾向性的先验,则对小效应不利。所以贝叶斯遭受质疑的其中一个点就在于先验假设可能会起到过于重要的作用。当然贝叶斯学者也在建立相应的应对措施——稳健性分析(Bayesian robustness check),用以查看贝叶斯因子受不同的先验分布尺度影响的程度。
2. 贝叶斯推断非常取决于哪些先验假设被纳入考虑。比如,H1(有效果)与H0(没有效果)在二分推断的基础上累积证据,贝叶斯因子反映的是这两个假设的‘相对’ 解释力。又比如用贝叶斯做ANOVA分析,贝叶斯因子反映的是这多个模型的相对解释力,然而可能这几个模型表现的都很一般,却因为做比较的模型很不契合而得到很高的贝叶斯因子。由此看来, ‘相对’也并不总是优势。
3. P值有p-hacking,相对的贝叶斯因子也有b-hacking的可能性,尤其是现如今研究者把连续的贝叶斯因子进行强度划分,可能会无意中促使研究结果为贝叶斯因子在3上下浮动的研究者采取一些小动作以期得到中等强度的证据。好在B-hacking相对而言没有p-hacking来的严重,因为贝叶斯因子的数值比强度类别划分更有解释力、受重视,并且JASP中的概率轮盘(proportionwheel)直接量化了各个假设的相对后验概率,而p值在显著水准下的二分解读使得p-hacking成为研究结论可信度的一大隐患。
至于p值,2018年,72位学者联名在《Nature·Human Behavior》上发表了一篇名为《重新定义统计意义》的文章,提出将统计显著性的阈值从0.05调整到0.005 (Benjamin et al., 2018)。作者认为,这是一个不完美的短期解决方案,却可以立即实施、一定程度上降低第一类错误,增进研究的可信度和可重复性。
IV. My opinions:
建议有时间的情况下、尤其是方法学背景或是对方法学感兴趣的同学可以适当接触贝叶斯统计推断, judge it after you are sufficiently exposed and see if it couldc onvince youJ.
在撰写研究结果的过程中,可以在p值后面附上贝叶斯因子作为补足从而加强解释力。借由免费.开放.无需编程背景、点击即可操作的统计软件JASP (JASP Team, 2019)这个可以轻易达成。JASP是一个为推进贝叶斯统计分析而开发的软件,目前可以进行大多数常见的统计分析,其他高级统计方法也在不断地纳入及完善,亦可用其进行传统基于p值的统计分析。
由于多数研究者在现阶段依旧采用Fisher的p值显著性检定,建议在解释结果时要重视p值的真正含义,尤其是在结果接近临界值时要更加谨慎。
V. 用JASP进行贝叶斯分析的学习参考资料
胡传鹏, 孔祥祯, Eric-Jan Wagenmakers, Alexander Ly, 彭凯平. (2018). 贝叶斯因子及其在JASP中的实现. 心理科学进展, 26(6),951-965.
van Doorn, J., Matzke, D., & Wagenmakers, E.-J. (in press). Anin-class demonstration of Bayesian inference. Psychology Learning and Teaching.
Correlation analysis
Marsman, M., & Wagenmakers, E.-J. (2017). Bayesian benefits with JASP. European Journal of Developmental Psychology, 14, 545-555.
Wagenmakers, E.-J., Morey, R. D., & Lee, M. D. (2016).Bayesian benefits for the pragmatic researcher. Current Directions inPsychological Science, 25, 169-176.
A/B Test:
Gronau, Q. F., Raj A., & Wagenmakers, E.-J. (2019). Informed Bayesian inference for the A/B test.
T-test:
Wagenmakers, E-J., Love, J., Marsman, M., Jamil, T., Ly, A.,Verhagen, J., ... Morey, R. D. (2018). Bayesian inference for psychology. PartII: Example applications with JASP. Psychonomic Bulletin & Review, 25(1),58-76.
Rouder, J. N., Speckman, P. L., Sun, D., Morey, R. D., &Iverson, G. (2009). Bayesian t tests for accepting and rejecting the null hypothesis. Psychonomic Bulletin &Review, 16, 225-237.
Meta-Analysis:
Gronau, Q. F., van Erp, S., Heck, D. W., Cesario, J., Jonas, K.J., & Wagenmakers, E.-J. (2017). A Bayesian model-averaged meta-analysis ofthe power pose effect with informed and default priors: The case of felt power. ComprehensiveResults in Social Psychology, 2, 123-138.
How to Report:
van Doorn, J., van den Bergh, D., Boehm, U., Dablander, F., Derks,K., Draws, T., Evans, N. J., Gronau, Q. F., Hinne, M., Kucharsky, S., Ly, A.,Marsman, M., Matzke, D., Komarlu Narendra Gupta, A. R., Sarafoglou, A., Stefan,A., Voelkel, J. G., & Wagenmakers, E.-J. (2019). The JASP guidelines forconducting and reporting a Bayesian analysis.
References:
Benjamin, D. J., Berger, J. O., Johannesson, M., Nosek, B. A.,Wagenmakers, E. J., Berk, R., ... Johnson, V. E. (2018). Redefinestatistical significance. Nature Human Behaviour, 2(1),6-10.
Chambers, C. (2017). The seven deadly sins of psychology: Amanifesto for reforming the culture of scientific practice. Princeton, NJ,US: Princeton University Press.
JASP Team (2019). JASP (Version 0.11.1) [Computer software].
Jeffreys, H. (1961). Theoryof Probability. Oxford, UK: Oxford University Press, 3rd edn.
Lee, M. D.,& Wagenmakers, E.-J. (2013). Bayesian cognitive modeling: A practical course. CambridgeUniversity Press.
Lindley, D. V. (1993). The analysis ofexperimental data: The appreciation of tea and wine. Teaching Statistics, 15, 22–25.