数值分析之龙贝格求积法

花了一晚上的时间把数值分析里面定积分求解看懂了，累得早上头疼发烧。。。唉革命尚未成功啊！

利用Richardson外推算法，得到如下的求积方法，其只产生四个序列：

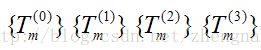
即：

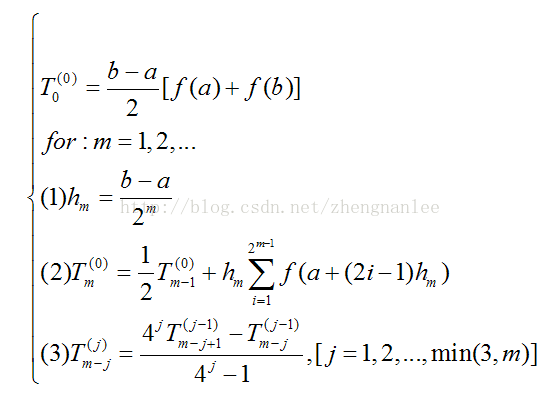
其结束迭代准则为：

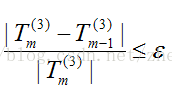
并认为为所求积分近似值。

有一定数值分析基础，不难写出如下程序

#include <iostream>
#include <stdlib.h>
#include <math.h>
#include <iomanip>

using namespace std;

///#define f(x) (sin(x))

double f(double x)
{
    return sin(x) / x;
}

double Romberg(double a, double b, int MAX_N, int DFS_N, double eps, double (*f)(double x))
{
    double n = DFS_N, h = (b-a) / n, s = 0;
    double t[MAX_N][MAX_N];
    bool flag = false;

    for(int i = 1; i < n; i++)
    {
        s += f(a + i * h);
    }

    t[0][1] = h * (s + (f(a)+f(b))/2);
    n *= 2;

    for(int m = 1; m < MAX_N; m++)
    {
        for(int i = 0; i < m; i++)
        {
            t[i][0] = t[i][1];
        }

        h = (b-a)/n;
        s = 0;

        for(int j = 1; j < n; j++)
        {
            s += f(a+j*h);
        }

        t[0][1] = h * (s + (f(a) + f(b))/2.0);
        n *= 2;

        for(int i = 1; i <= m; i++)
        {
            t[i][1] = t[i-1][1] + (t[i-1][1] - t[i-1][0])/(pow(2.0,2*m)-1);
        }

        if(abs(t[m][1] - t[m-1][1]) < eps)
        {
            cout << fixed << setprecision((int)(-log10(eps))) << t[m][1] << endl;
            flag = true;
            break;
        }
    }
    if(!flag)
    {
        cerr << "No solution!" << endl;
    }
}
int main()
{
    Romberg(1,2,500,100,0.00000000001,f);///start integral from a to b
}