炫云:线性代数4——向量3(叉积)
炫云:线性代数3——向量2(点积)
炫云:线性代数2——向量1(向量简介)
预备知识 矢量的叉乘
我们定义以下运算
为矢量
这个公式可由图 1记忆.
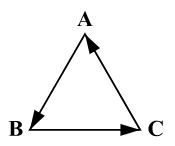
图中箭头的方向由叉乘的方向(顺时针或逆时针)决定,与内积无关, 即
注意即使将混合积省略括号记为
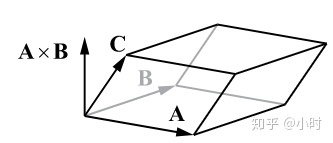
如图 2, 以三个矢量为棱作平行六面体. 可知
同理可得对于同一平行六面体
这里只证明了式 2的绝对值, 要证明正负号, 定义
代数法证明
预备知识 行列式
不难证明三矢矢积若展开成分量的形式,等于三个矢量组成的行列式
而利用行列式中任意两行置换符号改变,即可证明式 2.
版权声明:本文为weixin_35327824原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。