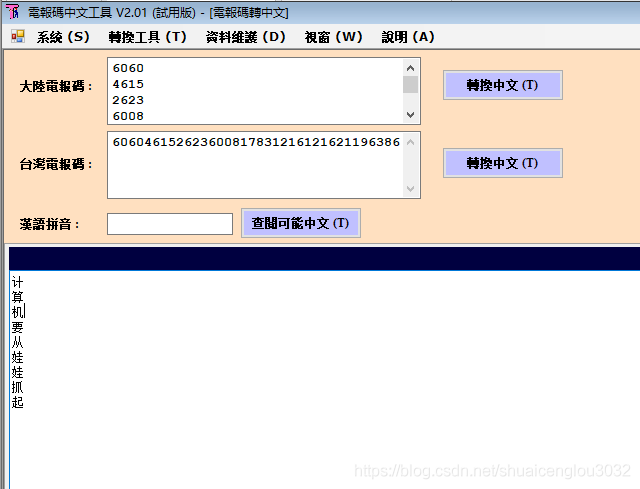
1、RSA1
直接上代码:
import gmpy2 as gp
p = 8637633767257008567099653486541091171320491509433615447539162437911244175885667806398411790524083553445158113502227745206205327690939504032994699902053229
q = 12640674973996472769176047937170883420927050821480010581593137135372473880595613737337630629752577346147039284030082593490776630572584959954205336880228469
dp = 6500795702216834621109042351193261530650043841056252930930949663358625016881832840728066026150264693076109354874099841380454881716097778307268116910582929
dq = 783472263673553449019532580386470672380574033551303889137911760438881683674556098098256795673512201963002175438762767516968043599582527539160811120550041
c = 24722305403887382073567316467649080662631552905960229399079107995602154418176056335800638887527614164073530437657085079676157350205351945222989351316076486573599576041978339872265925062764318536089007310270278526159678937431903862892400747915525118983959970607934142974736675784325993445942031372107342103852
n = p*q
phin = (p-1)*(q-1)
dd = gp.gcd(p-1, q-1)
d=(dp-dq)//dd * gp.invert((q-1)//dd, (p-1)//dd) * (q-1) +dq
print(d)
m = gp.powmod(c, d, n)
print('-------------------')
print(m)
print(hex(m)[2:])拿到十六进制的明文之后要转换成字符串:
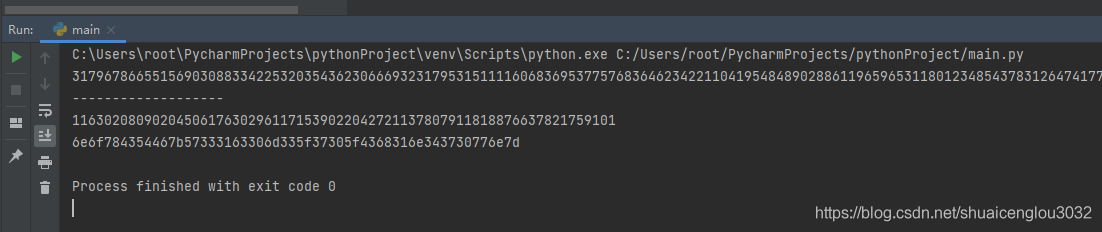
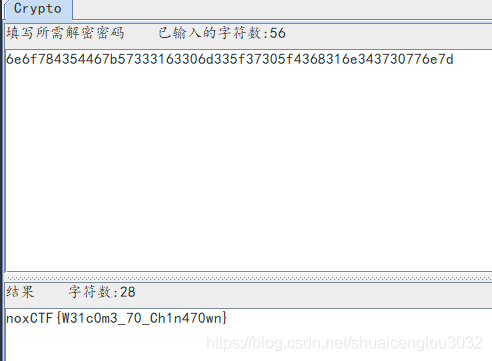
这里转换成字符串之后提交,不对。我又在外面加了一层flag{},也不对,最后灵机一动,把nnxCTF换成了flag,成功了。
2、RSA
解析RSA公钥:
openssl rsa -pubin -text -modulus -in pub.key:
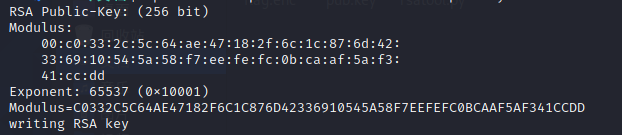
拿到N为:C0332C5C64AE47182F6C1C876D42336910545A58F7EEFEFC0BCAAF5AF341CCDD
爆破一下(这个比较耗时间,我R7的机器用了半个多小时才算出来,所以还是直接在线爆破吧):
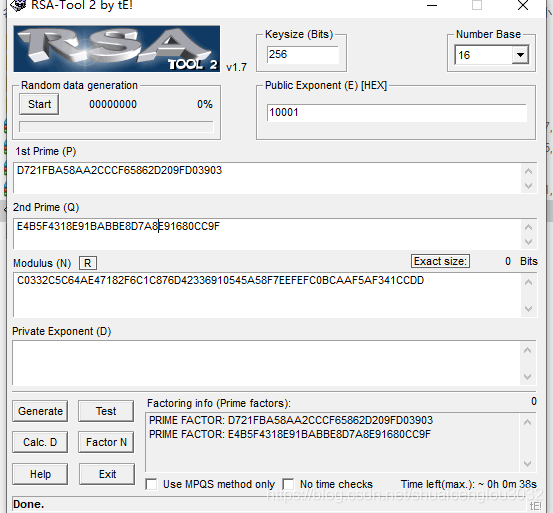
得到了p和q,然后上面可以看到e是65537.
所以就可以生成私钥并解密了:
python rsatool.py -f PEM -o key.key -p 1 -q 1 -e 1
openssl rsautl -decrypt -inkey key.pem -in flag.enc -out flag
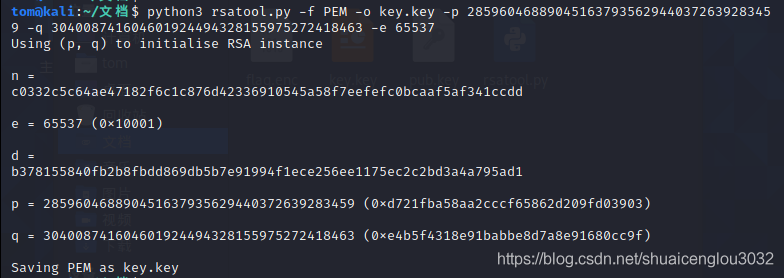
然后解密(这里记得把生成的key.key改成key.pem):
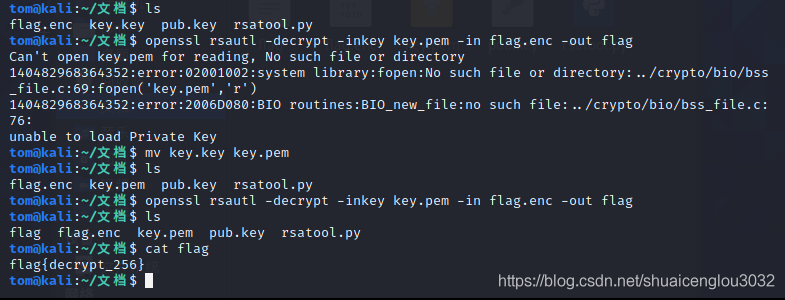
3、[NPUCTF2020]共 模 攻 击
先上hint的解密代码
from gmpy2 import *
from libnum import *
from sympy import *
p = 107316975771284342108362954945096489708900302633734520943905283655283318535709
n = 6807492006219935335233722232024809784434293293172317282814978688931711423939629682224374870233587969960713638310068784415474535033780772766171320461281579
e1 = 2303413961
c1 = 1754421169036191391717309256938035960912941109206872374826444526733030696056821731708193270151759843780894750696642659795452787547355043345348714129217723
e2 = 2622163991
c2 = 1613454015951555289711148366977297613624544025937559371784736059448454437652633847111272619248126613500028992813732842041018588707201458398726700828844249
s = gcdext(e1,e2)
c = pow(c1,s[1],n)*pow(c2,s[2],n) % n
print(c)
m = nthroot_mod(c,256,p)
print (hex(m))
print(n2s(m))得到明文:
m.bit_length() < 400
有点懵逼。看大佬的wp才知道是Coppersmith定理攻击。
4、[NCTF2019]easyRSA
直接上代码:
from gmpy2 import *
from Crypto.Util.number import *
from tqdm import tqdm
def onemod(p,r):
t = p-2
while pow(t, (p-1) // r, p) == 1: t -= 1
return pow(t, (p-1) // r, p)
def solution(p,root):
g = onemod(p, 0x1337)
may = []
for i in range(0x1337):
if i % 100 == 0:
print(i)
may.append(root * pow(g,i,p) % p)
return may
c = 10562302690541901187975815594605242014385201583329309191736952454310803387032252007244962585846519762051885640856082157060593829013572592812958261432327975138581784360302599265408134332094134880789013207382277849503344042487389850373487656200657856862096900860792273206447552132458430989534820256156021128891296387414689693952047302604774923411425863612316726417214819110981605912408620996068520823370069362751149060142640529571400977787330956486849449005402750224992048562898004309319577192693315658275912449198365737965570035264841782399978307388920681068646219895287752359564029778568376881425070363592696751183359
p = 199138677823743837339927520157607820029746574557746549094921488292877226509198315016018919385259781238148402833316033634968163276198999279327827901879426429664674358844084491830543271625147280950273934405879341438429171453002453838897458102128836690385604150324972907981960626767679153125735677417397078196059
q = 112213695905472142415221444515326532320352429478341683352811183503269676555434601229013679319423878238944956830244386653674413411658696751173844443394608246716053086226910581400528167848306119179879115809778793093611381764939789057524575349501163689452810148280625226541609383166347879832134495444706697124741
e = 0x1337
n = p * q
c_p = pow(c, (1 + 3307 * (p - 1) // e) // e, p)
C1 = solution(p, c_p)
c_q = pow(c, (1 + (2649 * (q - 1) // e)) // e, q)
C2 = solution(q, c_q)
a = invert(p, q)
b = invert(q, p)
flag=0
for i in tqdm(C1):
for j in tqdm(C2):
flag += 1
if flag % 1000000 == 0:
print(flag)
x = (b * q * i + a * p * j) % n
print(x)
if b"NCTF{" in long_to_bytes(x):
print(long_to_bytes(x))
exit()
这道题非常难,可以说是数学的交锋了,看了wp才知道简直是有毒,直接上出题人的wp了(原链接在这里):
我们知道,RSA对参数的一个要求就是,e和phi(n)一定要互素。这是为了要让e在模phi(n)下存在逆元d,进而可以直接pow(c, d, n)来解密。
那如果e和phi(n)不互质就会无解么?不,事实上,有解而且不止有一解。
这一题就是基于这个观察而出的。
题面十分简洁,甚至都给出了p, q。乍一看,肯定觉得这是一道送分题,然而事实远非如此。
正常情况下的RSA都要求e和phi(n)要互素,不过也有一些e和phi(n)有很小的公约数的题目,这些题目基本都能通过计算e对phi(n)的逆元d来求解。
然而本题则为e和p-1(或q-1)的最大公约数就是e本身,也就是说e | p-1,只有对c开e次方根才行。
可以将同余方程
$$
m^e \equiv c \quad (\text{mod}\ n)
$$
化成
$$
\begin{aligned}
m^e &\equiv c \quad (\text{mod}\ p)\newline
m^e &\equiv c \quad (\text{mod}\ q)
\end{aligned}
$$
然后分别在GF(p)和GF(q)上对c开e=0x1337次方根,再用CRT组合一下即可得到在mod n下的解。
问题是,如何在有限域内开根?
这里e与p-1和q-1都不互素,不能简单地求个逆元就完事。
这种情况下,开平方根可以用Tonelli–Shanks algorithm,wiki说这个算法可以扩展到开n次方根。
在这篇paper里给出了具体的算法:Adleman-Manders-Miller rth Root Extraction Method
应该还有其他的算法。。不过这一个对我来说比较容易去implement。

这个算法只能开出一个根,实际上开0x1337次方,最多会有0x1337个根(这题的情况下有0x1337个根)。
如何找到其他根?
StackOverflow – Cube root modulo P给出了方法:
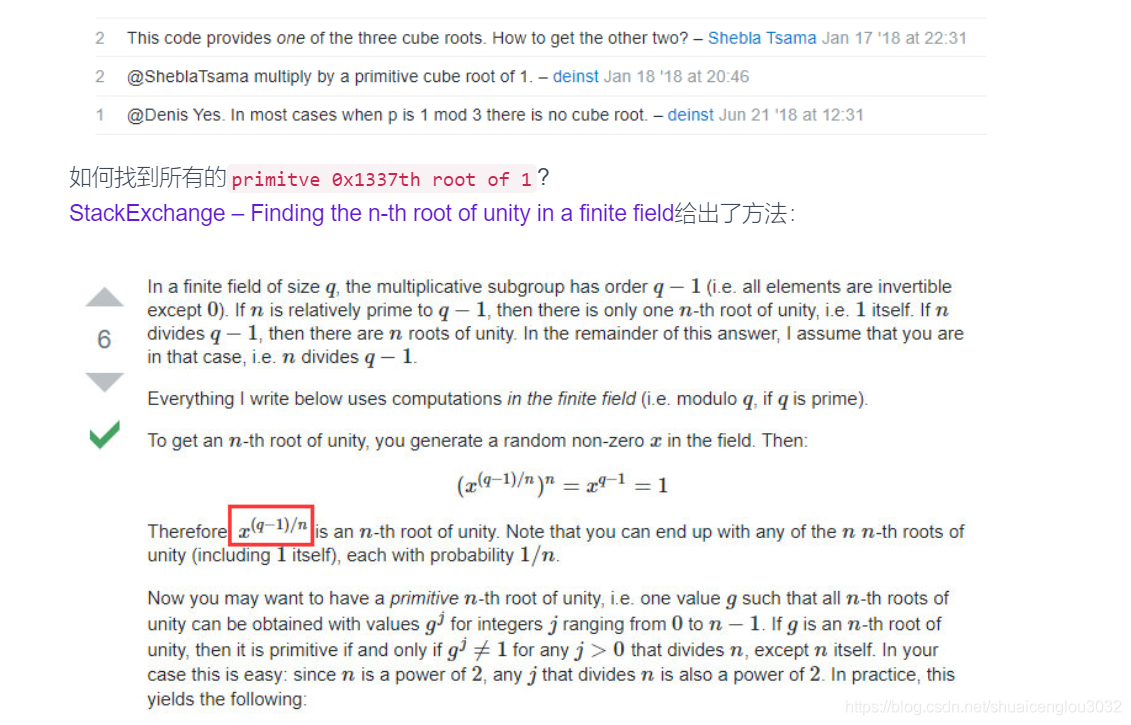
Exploit
- 先用
Adleman-Manders-Miller rth Root Extraction Method在GF(p)和GF(q)上对c开e次根,分别得到一个解。大概不到10秒。 - 然后去找到所有的
0x1336个primitive nth root of 1,乘以上面那个解,得到所有的0x1337个解。大概1分钟。 - 再用
CRT对GF(p)和GF(q)上的两组0x1337个解组合成mod n下的解,可以得到0x1337**2==24196561个mod n的解。最后能通过check的即为flag。大概十几分钟。 exp.sage如下:import random import time # About 3 seconds to run def AMM(o, r, q): start = time.time() print('\n----------------------------------------------------------------------------------') print('Start to run Adleman-Manders-Miller Root Extraction Method') print('Try to find one {:#x}th root of {} modulo {}'.format(r, o, q)) g = GF(q) o = g(o) p = g(random.randint(1, q)) while p ^ ((q-1) // r) == 1: p = g(random.randint(1, q)) print('[+] Find p:{}'.format(p)) t = 0 s = q - 1 while s % r == 0: t += 1 s = s // r print('[+] Find s:{}, t:{}'.format(s, t)) k = 1 while (k * s + 1) % r != 0: k += 1 alp = (k * s + 1) // r print('[+] Find alp:{}'.format(alp)) a = p ^ (r**(t-1) * s) b = o ^ (r*alp - 1) c = p ^ s h = 1 for i in range(1, t): d = b ^ (r^(t-1-i)) if d == 1: j = 0 else: print('[+] Calculating DLP...') j = - dicreat_log(a, d) print('[+] Finish DLP...') b = b * (c^r)^j h = h * c^j c = c ^ r result = o^alp * h end = time.time() print("Finished in {} seconds.".format(end - start)) print('Find one solution: {}'.format(result)) return result def findAllPRoot(p, e): print("Start to find all the Primitive {:#x}th root of 1 modulo {}.".format(e, p)) start = time.time() proot = set() while len(proot) < e: proot.add(pow(random.randint(2, p-1), (p-1)//e, p)) end = time.time() print("Finished in {} seconds.".format(end - start)) return proot def findAllSolutions(mp, proot, cp, p): print("Start to find all the {:#x}th root of {} modulo {}.".format(e, cp, p)) start = time.time() all_mp = set() for root in proot: mp2 = mp * root % p assert(pow(mp2, e, p) == cp) all_mp.add(mp2) end = time.time() print("Finished in {} seconds.".format(end - start)) return all_mp c = 10562302690541901187975815594605242014385201583329309191736952454310803387032252007244962585846519762051885640856082157060593829013572592812958261432327975138581784360302599265408134332094134880789013207382277849503344042487389850373487656200657856862096900860792273206447552132458430989534820256156021128891296387414689693952047302604774923411425863612316726417214819110981605912408620996068520823370069362751149060142640529571400977787330956486849449005402750224992048562898004309319577192693315658275912449198365737965570035264841782399978307388920681068646219895287752359564029778568376881425070363592696751183359 p = 199138677823743837339927520157607820029746574557746549094921488292877226509198315016018919385259781238148402833316033634968163276198999279327827901879426429664674358844084491830543271625147280950273934405879341438429171453002453838897458102128836690385604150324972907981960626767679153125735677417397078196059 q = 112213695905472142415221444515326532320352429478341683352811183503269676555434601229013679319423878238944956830244386653674413411658696751173844443394608246716053086226910581400528167848306119179879115809778793093611381764939789057524575349501163689452810148280625226541609383166347879832134495444706697124741 e = 0x1337 cp = c % p cq = c % q mp = AMM(cp, e, p) mq = AMM(cq, e, q) p_proot = findAllPRoot(p, e) q_proot = findAllPRoot(q, e) mps = findAllSolutions(mp, p_proot, cp, p) mqs = findAllSolutions(mq, q_proot, cq, q) print mps, mqs def check(m): h = m.hex() if len(h) & 1: return False if h.decode('hex').startswith('NCTF'): print(h.decode('hex')) return True else: return False # About 16 mins to run 0x1337^2 == 24196561 times CRT start = time.time() print('Start CRT...') for mpp in mps: for mqq in mqs: solution = CRT_list([int(mpp), int(mqq)], [p, q]) if check(solution): print(solution) print(time.time() - start) end = time.time() print("Finished in {} seconds.".format(end - start))Summary
p, q都是预先用下面这个函数生成的,保证了e | p-1, e | q-1。import random from Crypto.Util.number import * def gen(): p = e * random.getrandbits(1012) + 1 while not isPrime(p): p = e * random.getrandbits(1012) + 1 return p而且
p-1, q-1的ord(e) = 1,使得Adleman-Manders-Miller rth Root Extraction Method中无需计算DLP。降低了题目难度。flag后面填充了一段杂乱的字符串,是为了增加flag转成整数后的位数。不然位数太低,算出GF(p)和GF(q)里2组0x1337个解,取交集就可以得到flag了。位数增加后,就必须要算24196561次CRT才能得到flag,可能需要个十几分钟来跑。------------------------------无话可说,给出题人跪下了-------------------------------------------------
5、丢失的MD5
我还以为要写代码穷举,结果一条命令搞定
python md5.py
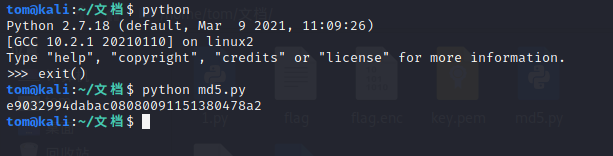
加上flag就是答案。
6、Alice与Bob
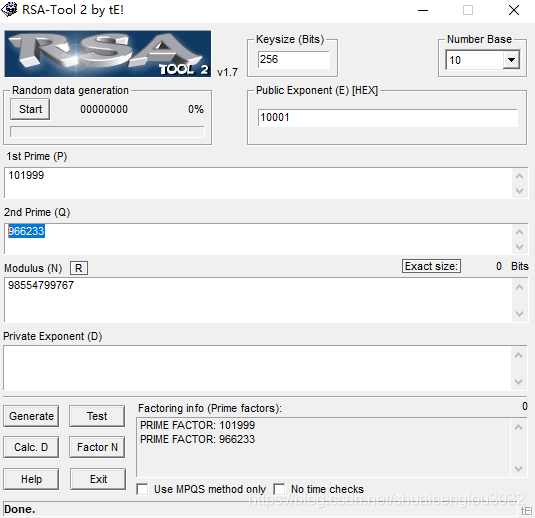
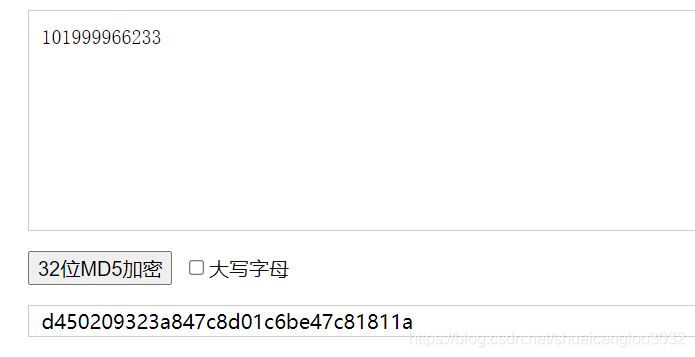
密码学历史中,有两位知名的杰出人物,Alice和Bob。他们的爱情经过置换和轮加密也难以混淆,即使是没有身份认证也可以知根知底。就像在数学王国中的素数一样,孤傲又热情。下面是一个大整数:98554799767,请分解为两个素数,分解后,小的放前面,大的放后面,合成一个新的数字,进行md5的32位小写哈希,提交答案。 注意:得到的 flag 请包上 flag{} 提交
粗暴:
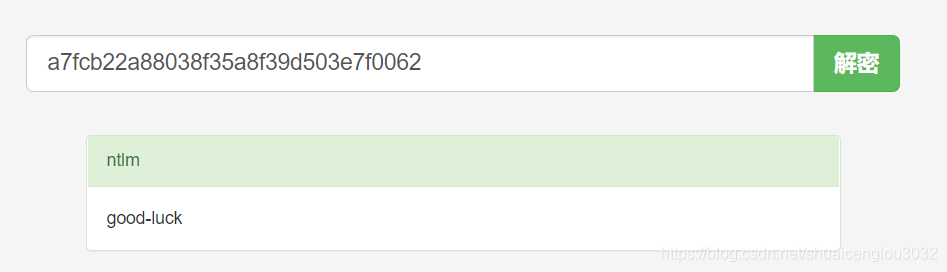
7、WIndows系统密码
8、传统知识+古典密码
将题目中的内容和天干地支的顺序对应,得出一数字字符:28 30 23 8 17 10 16 30,但题目中还提到 “信的背面还写有“+甲子”,”,然后各加六十(一甲子代表60年),变成 88 90 83 68 77 70 76 90;与ASII码一一对应得 XZSDMFLZ,然后再来凯撒一波,得到flag{SHUANGYU}
9、传感器
5555555595555A65556AA696AA6666666955
这是某压力传感器无线数据包解调后但未解码的报文(hex)
已知其ID为0xFED31F,请继续将报文完整解码,提交hex。
提示1:曼联
根据提示及大佬的wp知道是曼彻斯特编码
先转二进制:
10101010101010101010101010101011001010101010101010110100110010101010101011010101010011010010110101010100110011001100110011001100110100101010101
IEEE 802.4(令牌总线)和低速版的IEEE 802.3(以太网)中规定, 按照这样的说法, 01电平跳变表示1, 10的电平跳变表示0。
然后每两位根据上述规则转为0或者1,再转十六进制即可,此处给出大佬的代码:
cipher='5555555595555A65556AA696AA6666666955'
def iee(cipher):
tmp=''
for i in range(len(cipher)):
a=bin(eval('0x'+cipher[i]))[2:].zfill(4)
tmp=tmp+a[1]+a[3]
print(tmp)
plain=[hex(int(tmp[i:i+8][::-1],2))[2:] for i in range(0,len(tmp),8)]
print(''.join(plain).upper())
iee(cipher)
运行就能拿到flag。
9.1、传感器1
这里另外给出一道差分曼彻斯特编码的题:
已知ID为0x8893CA58的温度传感器的未解码报文为:3EAAAAA56A69AA55A95995A569AA95565556
此时有另一个相同型号的传感器,其未解码报文为: 3EAAAAA56A69AA556A965A5999596AA95656
解码该报文得到flag。
先把已知ID的报文转二进制:
1111101010101010101010101001010110101001101001101010100101010110101001010110011001010110100101011010011010101010010101010101100101010101010110
这题是差分曼彻斯特编码,和上面第九题稍有不同,识别差分曼彻斯特编码的方法:主要看两个相邻的波形,如果后一个波形和前一个的波形相同,则后一个波形表示0,如果波形不同,则表示1。
因此上面的二进制四个一组的看,一组中前两个等于后两个则转换成0,不同转换成1:
1111 1010
上代码:
a = 0x3EAAAAA56A69AA55A95995A569AA95565556
b = 0x3EAAAAA56A69AA556A965A5999596AA95656
b2 = bin(b)
print len(b2)
str = ""
for i in range(len(b2[2:]) / 2):
a1 = b2[i * 2:i * 2 + 2]
a2 = b2[i * 2 + 2:i * 2 + 4]
if a2 != '10' and a2 != '01':
continue
if a1 != '10' and a1 != '01':
continue
if a1 != a2:
str += '1'
else:
str += '0'
print len(str)
print hex(int(str, 2)).upper()
# 0X10024D8893CA584181L
# 0X30024D8845ABF34119L10、信息化时代的步伐
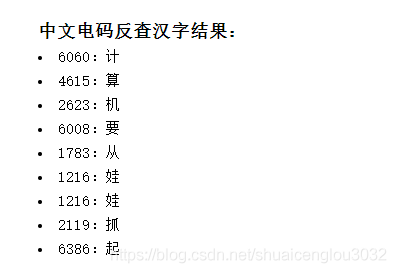
本地工具: