简述最优二叉树（赫夫曼树）

什么是哈夫曼树：
给定N个权值作为N个叶子结点，构造一棵二叉树，若该树的带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树，权值较大的结点离根较近。

哈夫曼树被用来进行哈夫曼编码，下面来介绍哈夫曼编码：
假设需要传送的电文为“ABACCDA”，它只有四种字符，只需要用两个字符的串就可以分辨，假设A,B,C,D的编码分别是00，01,10,11，则该电文的编码便是：“00010010101100”，总长为14位，对方接收时，只需要二位一分就可以进行译码。在现实中尽可能希望编码总长尽可能短，如果采用对每个字符设计长度不同的编码，那么让电文中出现次数较多的字符尽可能采用短的编码，那么电文总长就可以减少。比如设计A,B,C,D的编码为0,00,1，01，则上述电文可转换为：“000011010”，总长为9。但是这样的电文无法翻译，例如“0000”就有多种译法。或是“AAAA”，或者是“ABA”，又或者是“BB”等，因此，若要设计长度不等的编码，则必须是任一个字符的编码都不是另一个字符的编码的前缀，这种编码称为前缀编码

那么如何得到电文长度最短的二进制前缀编码呢？设计电文总长度最短的二进制前缀编码即为以n种字符出现的频率做权值，设计一棵哈夫曼树的问题，由此得到的二进制前缀编码称为哈夫曼码。

下面就来说说如何创建一棵赫夫曼树。

对于如何构造哈夫曼树，哈夫曼最早就给出了一个带有一般规律的算法，俗称哈夫曼算法：

（1）根据给定的n个权值{$w_1$,$w_2$……,$w_n$}构成n棵二叉树的集合F = {$T_1$,$T_2$……，$T_n$},其中每棵二叉树中的$T_i$中只有一个带权为$w_i$的根节点，其左右子树均为空。

（2）在F中选取两棵根节点的权值最小的树作为左右子树构成一棵新的二叉树，且置新的二叉树的根节点的权值为其左右子树上根节点的权值之和；

（3）在F中删除这两棵树，同时将新得到的二叉树加入F中；

（4）重复（2），和（3）步骤，直到F只含有一棵树为止。则这棵树就是哈夫曼树。

下面来看一个简单的案例：字母{a,b,c,d}，出现的次数为{7,5,2,4},构建出哈夫曼树：

我们按照哈夫曼算法来构建哈夫曼树。
第一步选取其中最小的两个构建成二叉树：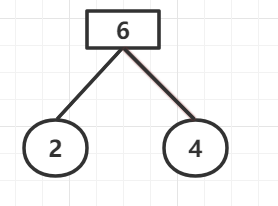

第二步将6添加至权值序列中，删除之前的2和4：
权值列表变成{7，5，6}
重复第一二步，直到构建完成：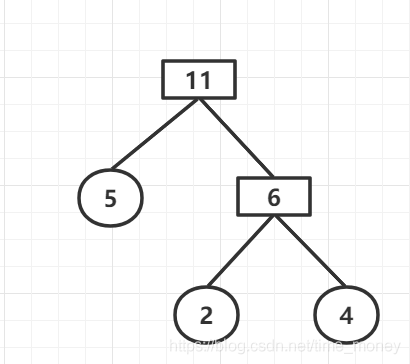

权值列表：{7,11}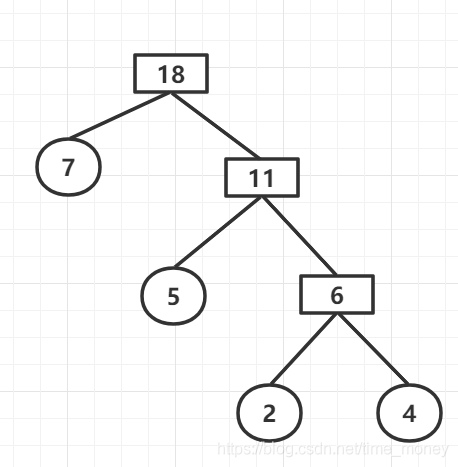

至此，哈夫曼树构建完成：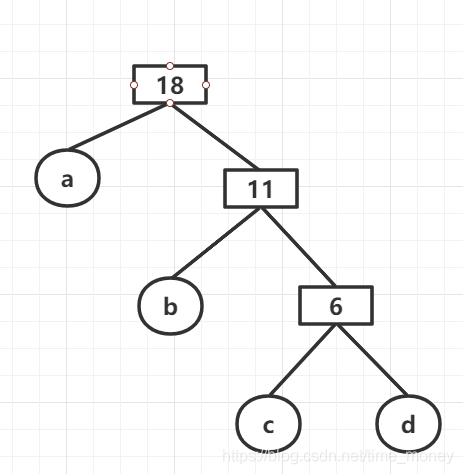

带权路径长度为：WPL = 7x1 + 5x2 + 2x3 + 4x3 = 35
当然，哈夫曼树不是唯一的，比如上面的哈夫曼树也可以为：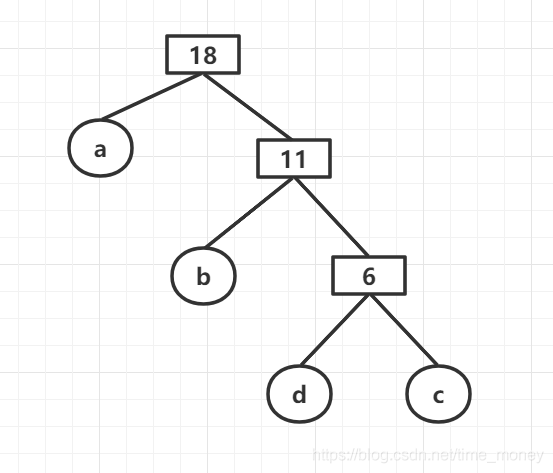

带权路径长度为：WPL = 7x1 + 5x2 + 2x3 + 4x3 = 35

但是不管哈夫曼树怎样构造，最短带权路径长度只有一个。

由于哈夫曼树中没有度为1的结点（又叫做正则二叉树），则一棵有n个叶子结点的哈夫曼树共有2n-1个结点，可以存储在哎一个大小为2n-1的一维数组中。

下面来看一个复杂的例题：
已知某系统的通信联络中只可能出现8中字符，次数别为w= {5，29，7，8，14，23，3，11}
按照哈夫曼算法来构建哈夫曼树：
权值列表：{3，5，7，8，11，14，23，29}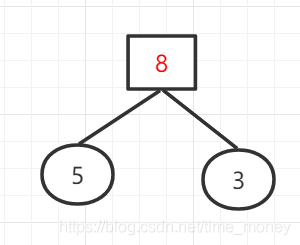

权值列表：{7，8，8，11，14，23，29}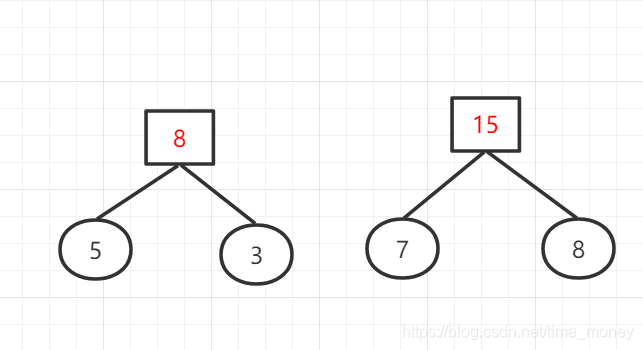

权值列表：{8，11，14，15，23，29}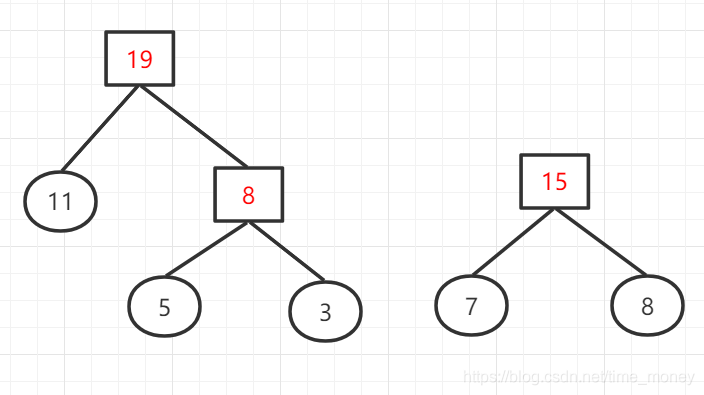

权值列表：{14，15，19，23，29}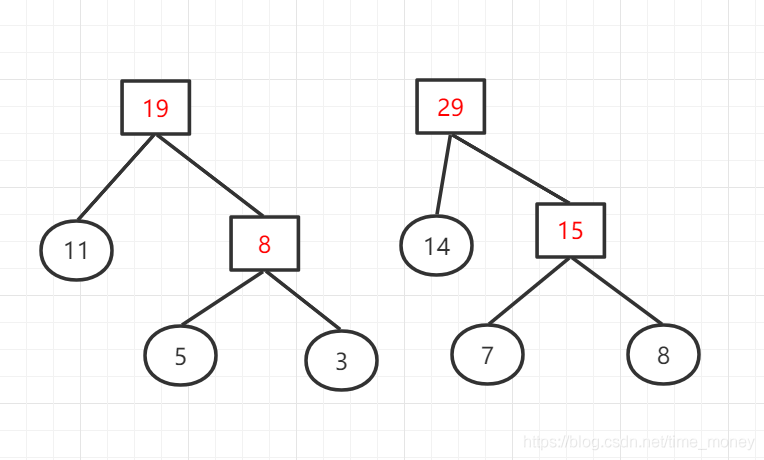

权值列表：{19，23，29，29}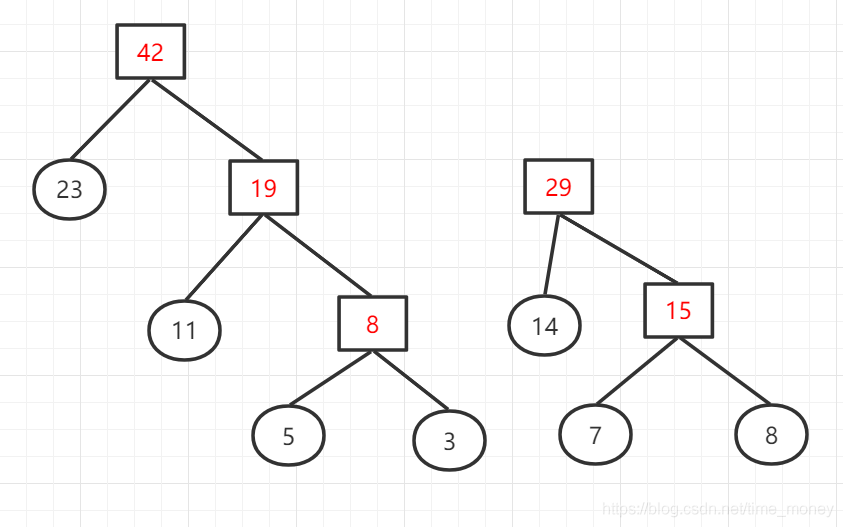

权值列表：{29，29，42}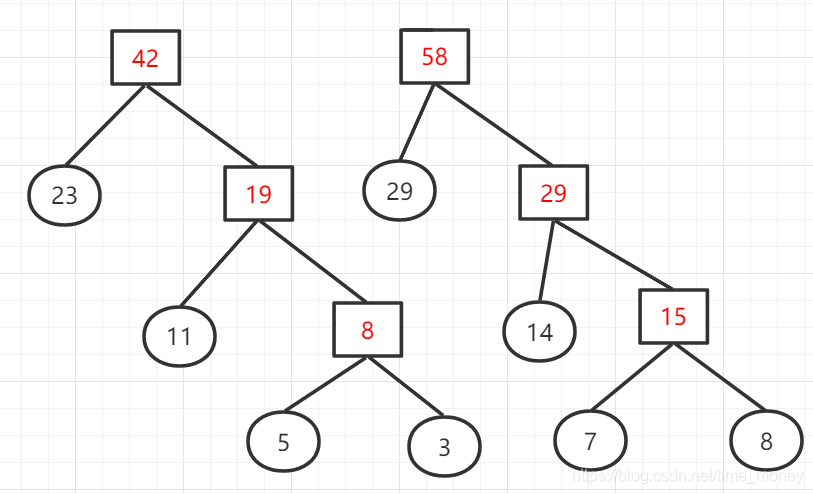

权值列表：{42，58}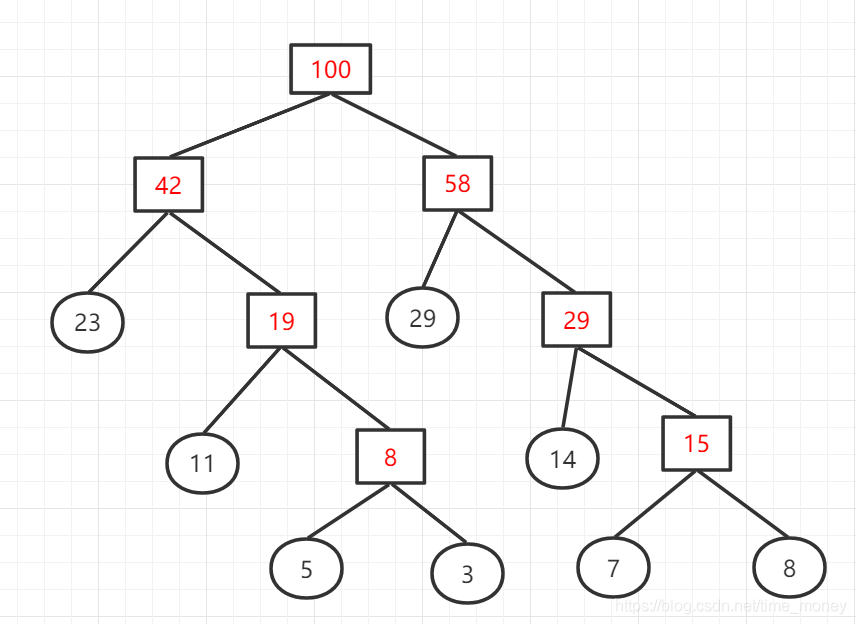

至此，哈夫曼树已经构建完成。我们来算算其带权路径：
WPL = 23x2 + 11x3 + 5x4 + 3x4 + 29x2 + 14x3 + 7x4 + 8x4 = 271
我们规定向左为0，向右为1，则，该哈夫曼树为：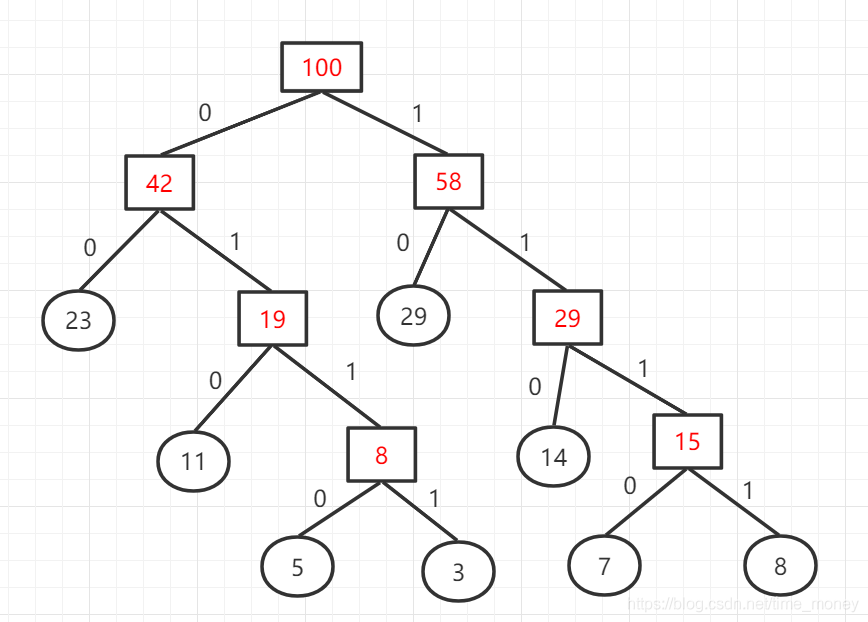

则这八种字符的编码分别为：{0110，10，1110，1111，110，00，011，010}

当然构造出的哈夫曼树不止一种，也可能为：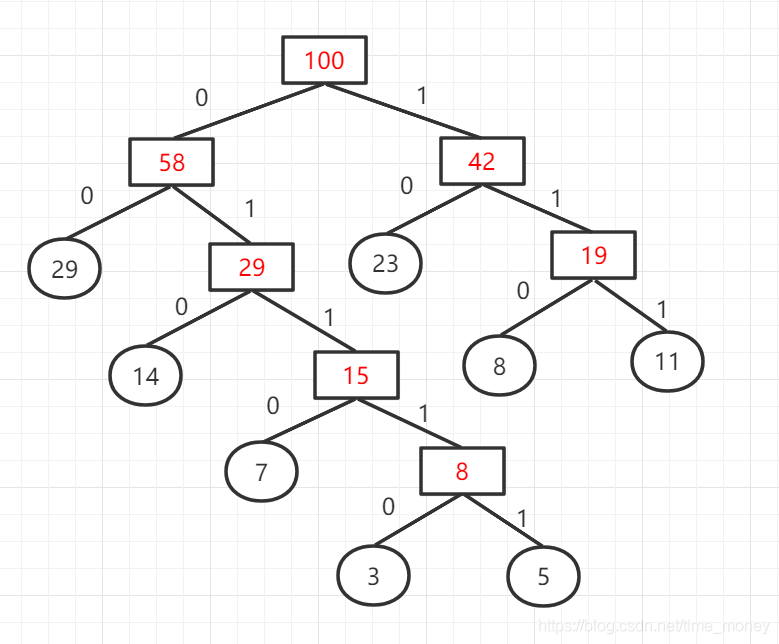
该图的带权路径为:
WPL = 29x2 + 14x3 + 7x4 + 3x5 + 5x5 + 23x2 + 8x3 + 11x3 = 271
由此看出，哈夫曼树可能不同，但是带权路径一定是同一个最小值。

已经了解了思想了，现在该如何实现了。

class Node:
    def __init__(self, name, weight):
        self.name = name #节点名
        self.weight = weight #节点权重
        self.left = None #节点左孩子
        self.right = None #节点右孩子
        self.father = None # 节点父节点
    #判断是否是左孩子
    def is_left_child(self):
        return self.father.left == self

#创建最初的叶子节点
def create_prim_nodes(data_set, labels):
    if(len(data_set) != len(labels)):
        raise Exception('数据和标签不匹配!')
    nodes = []
    for i in range(len(labels)):
        nodes.append( Node(labels[i],data_set[i]) )
    return nodes


# 创建huffman树
def create_HF_tree(nodes):
    #此处注意，copy()属于浅拷贝，只拷贝最外层元素，内层嵌套元素则通过引用，而不是独立分配内存
    tree_nodes = nodes.copy()
    while len(tree_nodes) > 1: #只剩根节点时，退出循环
        tree_nodes.sort(key=lambda node: node.weight)#升序排列
        new_left = tree_nodes.pop(0)
        new_right = tree_nodes.pop(0)
        new_node = Node(None, (new_left.weight + new_right.weight))
        new_node.left = new_left
        new_node.right = new_right
        new_left.father = new_right.father = new_node
        tree_nodes.append(new_node)
    tree_nodes[0].father = None #根节点父亲为None
    return tree_nodes[0] #返回根节点

#获取huffman编码
def get_huffman_code(nodes):
    codes = {}
    for node in nodes:
        code=''
        name = node.name
        while node.father != None:
            if node.is_left_child():
                code = '0' + code
            else:
                code = '1' + code
            node = node.father
        codes[name] = code
    return codes


if __name__ == '__main__':
    labels = ['A','B','C','D','E','F','G','H']
    data_set = [5,29,7,8,14,23,3,11]
    nodes = create_prim_nodes(data_set,labels)#创建初始叶子节点
    root = create_HF_tree(nodes)#创建huffman树
    codes = get_huffman_code(nodes)#获取huffman编码
    #打印huffman码
    for key in codes.keys():
        print(key,': ',codes[key])

运行结果：

A :  0001
B :  10
C :  1110
D :  1111
E :  110
F :  01
G :  0000
H :  001

代码参考自：哈夫曼树代码