21.动态规划整理

分割等和子集

分成元素和相等的两个部分,首先如果整体和为奇数肯定划分失败,因此需要排除此特殊情况,接下来按照背包问题进行递归分析:

当求出half值后,原本问题变成了,能否在数组中找到一组数字,使得他们的值为half,典型的背包问题,dp[i][j]表示,对于arr[0]...arr[i],能否找到一组数字的和刚好为j,写出递推关系:

dp[i][j]=dp[i-1][j] or dp[i-1][j-num[i-1]] 表示的是当前状态可以从不选入当前元素和选入当前元素两种选择中继承,但是此条件的成立条件首先是j>=num[i-1],当不满足此条件的时候dp[i][j]只能从不选入当前元素的状态继承

 public boolean canPartition(int[] nums) {
        int sum=Arrays.stream(nums).sum();
        if(sum%2!=0)return false;
        int half=sum/2;
        int n=nums.length;
        boolean[][] dp = new boolean[n+1][half + 1];
        dp[0][0]=true;
        for (int i = 1; i <=n; i++) {
            for (int j = 1; j <= half; j++) {
                dp[i][j]=dp[i-1][j];
                if(j>=nums[i-1]){
                    dp[i][j]=dp[i][j]||dp[i-1][j-nums[i-1]];
                }
            }
        }
        return dp[n][half];
    }

对二维的dp数组进行优化,由于dp[i][j]的状态只与dp[i-1][?]的状态有关,所以可以简化为一维数组,简化为一维数组过程中会产生问题,如果按照从小到大的顺序更新dp值,会导致在计算dp[j]的时候,dp[j-nums[i]]已经是被更新过的值,而不是我们需要的状态转移前的值

 public boolean canPartition(int[] nums) {
    int sum=Arrays.stream(nums).sum();
        if(sum%2!=0)return false;
        int half=sum/2;
        int n=nums.length;
        boolean[] dp = new boolean[half + 1];
        dp[0]=true;
        for (int i = 1; i <=n; i++) {
            for (int j = half; j > 0; j--) {
                if(j>=nums[i-1]){
                    dp[j]=dp[j]||dp[j-nums[i-1]];
                }
            }
        }
        return dp[half];
    }

此题我们可以总结出一个动态规划数组高维转低维的规律,如果dp[i]的状态由dp[j]转移而来,且i>j,则最好使用逆序来避免值的覆盖问题

加减的目标值

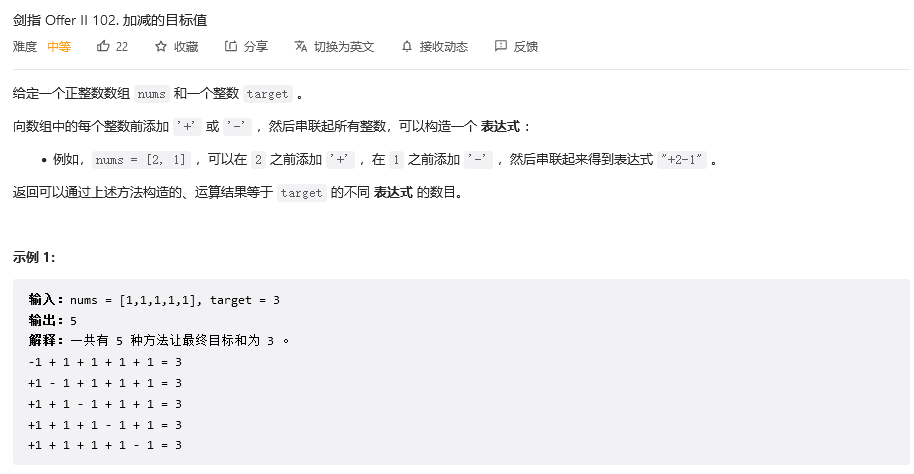
该问题是上一个问题的变种,记所有值的和为sum,负数的和为neg,目标值为target,正数和-负数和=target值:(sum-neg)-neg=target,直接变种为上一个问题,找到neg值即可

不同点在于,上一题只需要判断,这一题需要知道能有多少种方法dp[0][0]表示的是在数组为空,target为0的情况,我们让他=1,表示这也是一种方法,以此来进行后续的状态转移

• 在j<nums[i-1]的时候,状态只能由dp[i-1][j]继承而来,这和上一题没有区别
• 在j>=nums[i-1]的时候,状态可以由dp[i-1][j]和dp[i-1][j-nums[i-1]]继承而来,由于我们计算的是总次数,所以是他们的和(其实也和上一题一样,在bool运算中|就相当于和的概念)

 public int findTargetSumWays(int[] nums, int target) {
         int sum=Arrays.stream(nums).sum();
        int neg=sum-target;
        if(neg<0||neg%2==1)return 0;
         neg/=2;
        int n=nums.length;
        int[][] dp = new int[n + 1][neg + 1];
        dp[0][0]=1;
        for (int i = 1; i <=n; i++) {
            for (int j = 0; j <=neg ; j++) {
                dp[i][j]=dp[i-1][j];
                if(j>=nums[i-1]){
                    dp[i][j]+=dp[i-1][j-nums[i-1]];
                }
            }
        }
        return dp[n][neg];
    }

最少的硬币数目

与之前的题不同,现在每种硬币的数量是无限的,对于每个值,都遍历一边整个coin数组,就能达到金币无限的效果,由于与硬币的顺序无关,所以可以只使用一个一维数组

 public int coinChange(int[] coins, int amount) {
        int n=coins.length;
        int[] dp=new int[amount+1];
        Arrays.fill(dp,amount+1);
        dp[0]=0;
        for (int i = 1; i <=amount ; i++) {
            for (int coin : coins) {
                if(i>=coin)
                dp[i]=Math.min(dp[i],dp[i-coin]+1);
            }
        }
        return dp[amount]==amount+1?-1:dp[amount];
    }

排列的数目

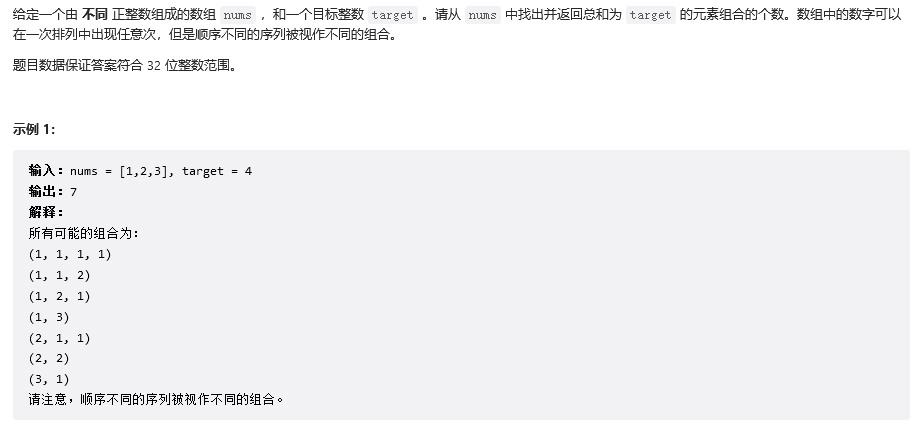
由于硬币数量无限,可以参考上题,但此题要求的是可能的组合数目,因此,每个dp[i]应该累加之前的结果,对于dp[0]表示的是,当target为0的时候出现的组合数,为了能有效的递推,应该将其设置为1,如果设为0的话,所有的值都是0

 public int combinationSum4(int[] nums, int target) {
        int n=nums.length;
        int[] dp = new int[target + 1];
        dp[0]=1;
        for (int i = 1; i <=target ; i++) {
            for (int num : nums) {
                if(i>=num){
                    dp[i]+=dp[i-num];
                }
            }
        }
        return dp[target];
    }