1、树的定义

树可以分为：非空树和空树（节点数为0）。
下图为非空树：

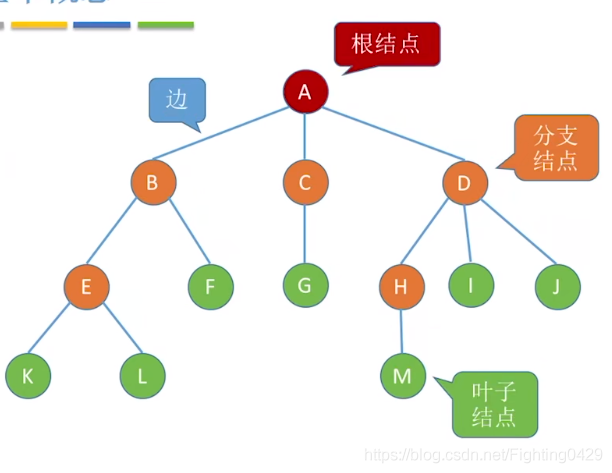
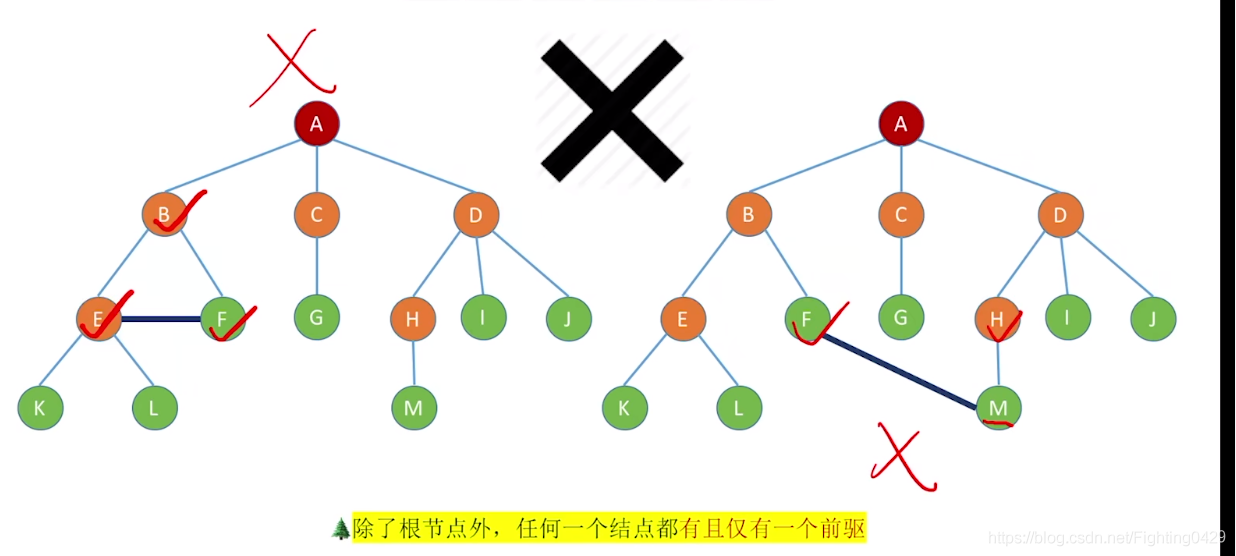
1.1、节点之间的关系描述

1.2、节点、树的属性描述

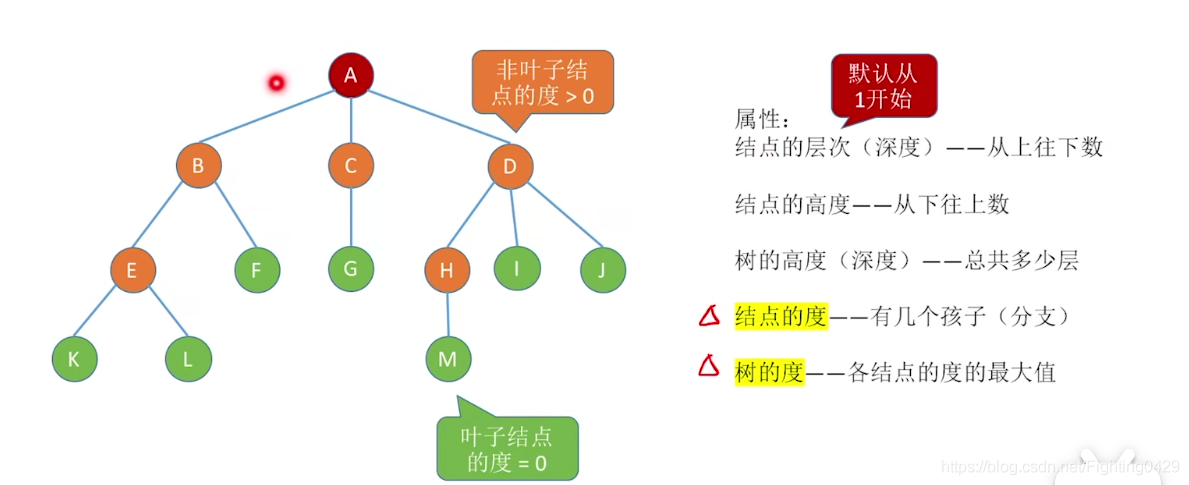
树的高度为4，树的度为3
B C D节点的高度为3，深度为2。
K L M的深度为4，高度为1。
C节点的度为1，G节点的度为0

1.3、有序树V.S无序树

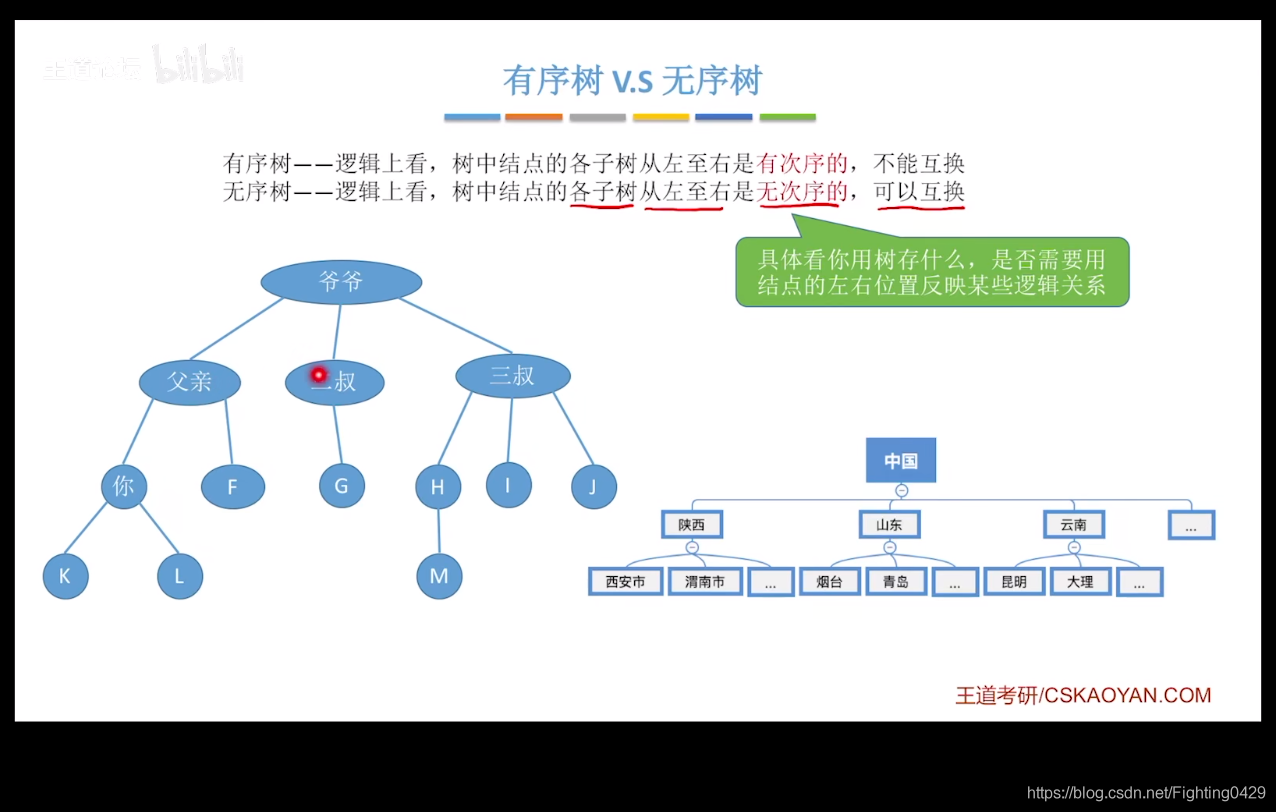
1.4、树和森林

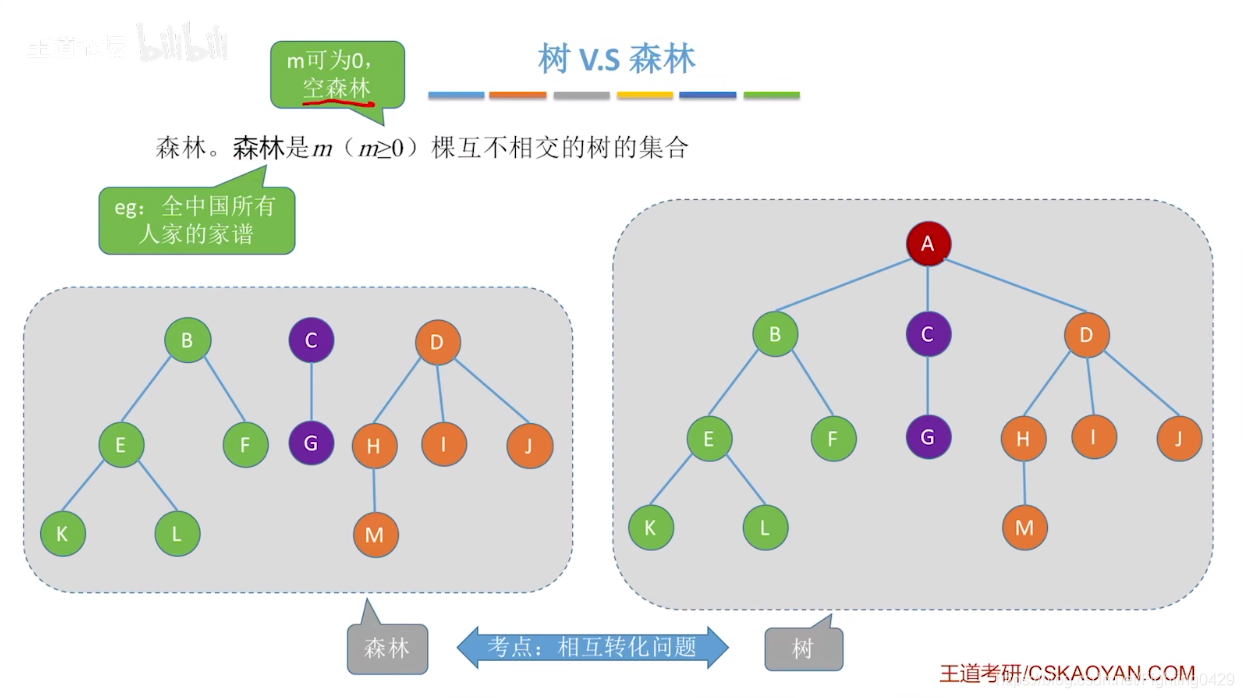
1.5、树的基本性质

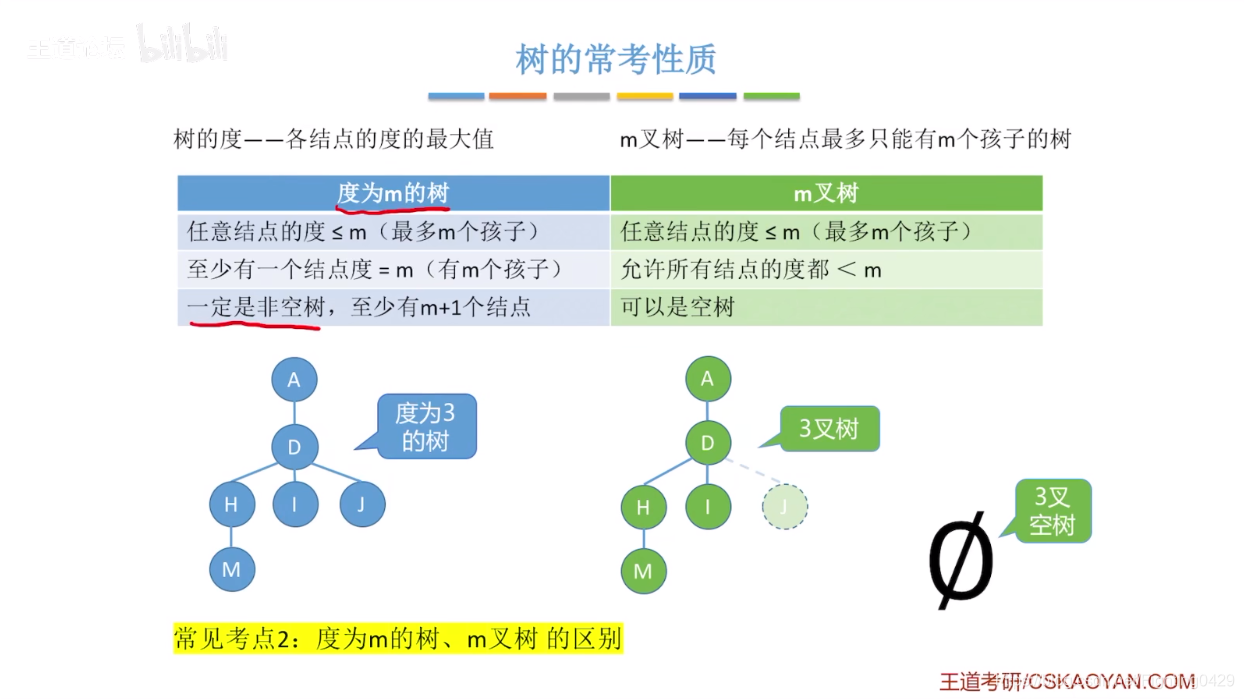
2、二叉树

2.1、二叉树的定义

2.1.1、基本概念

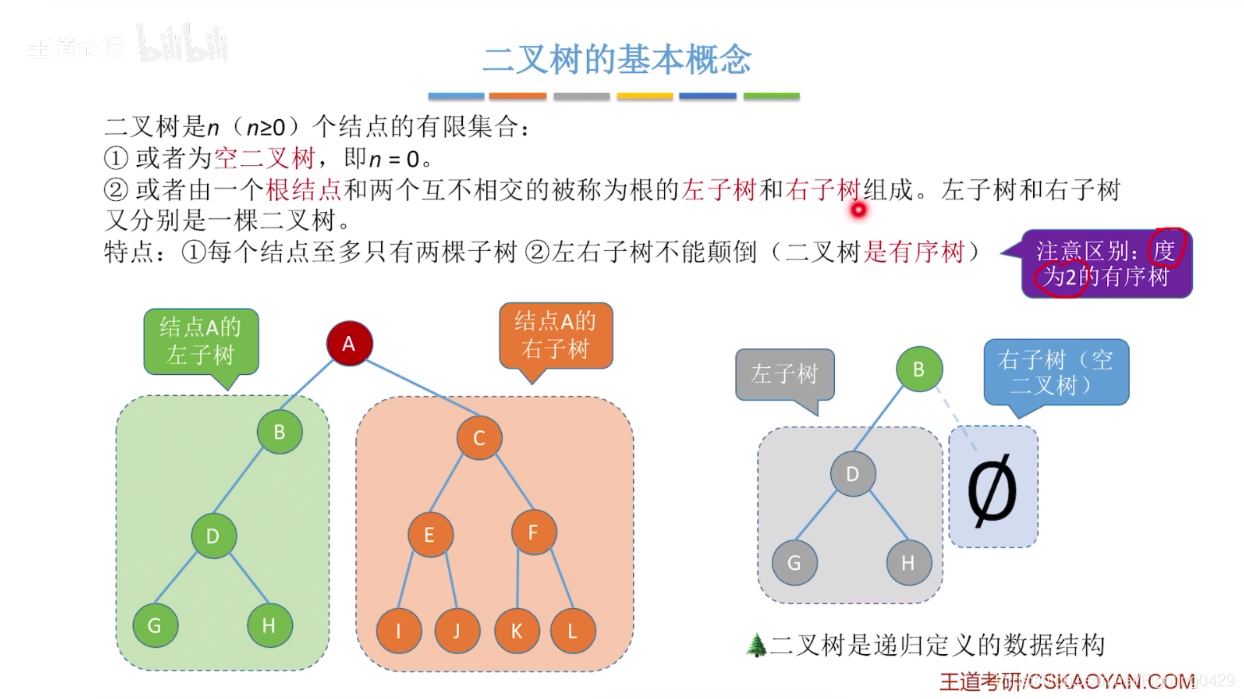
2.1.2、五种状态

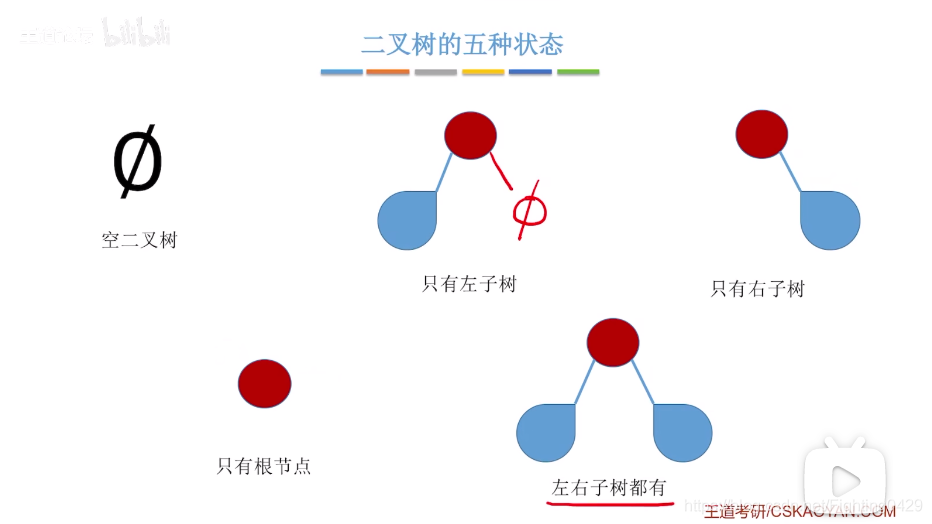
2.1.3、几个特殊的二叉树

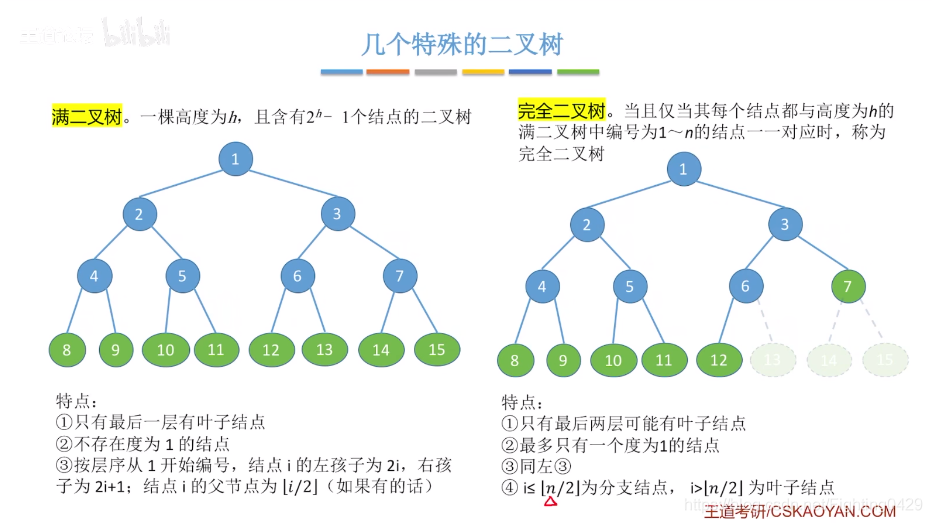
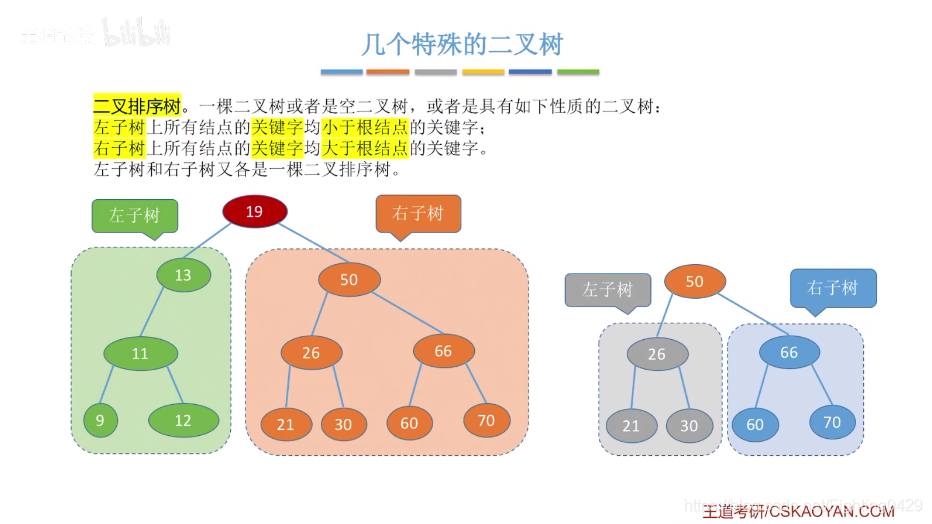
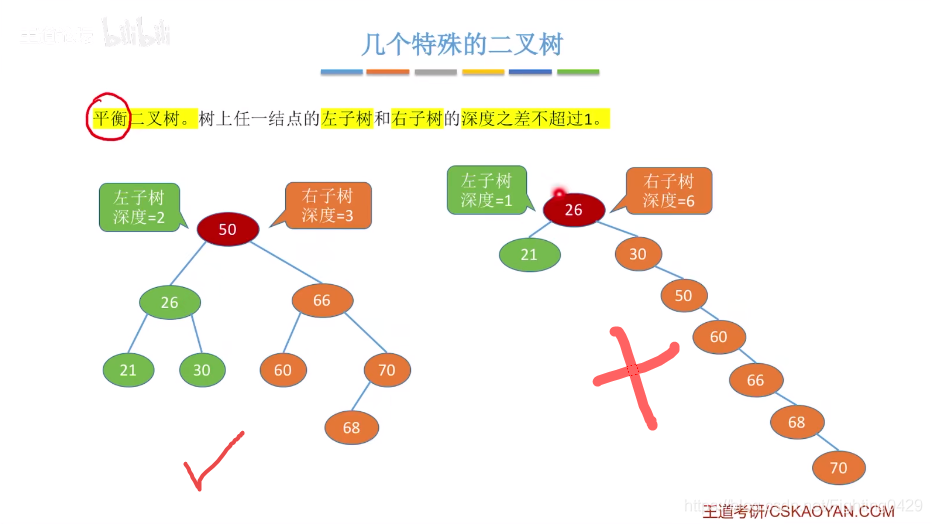
2.2、二叉树的存储结构

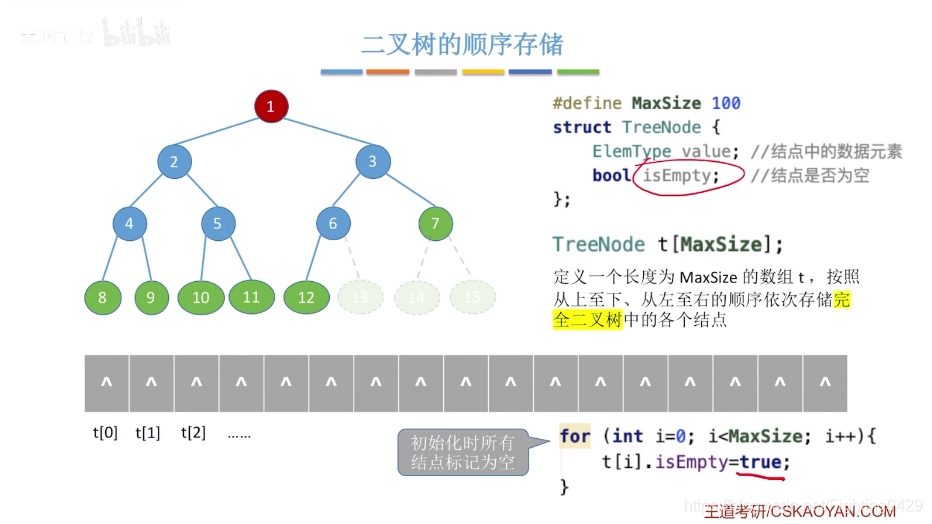
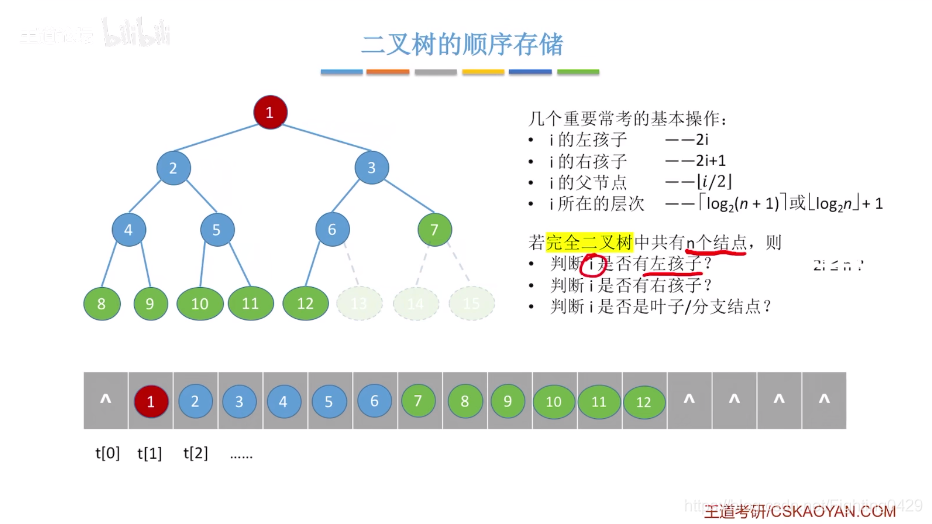
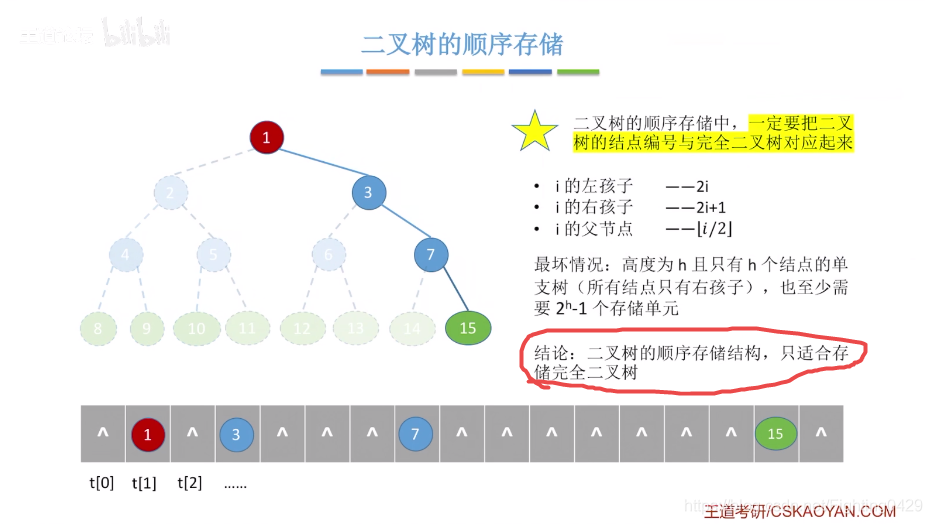
2.2.1、顺序存储

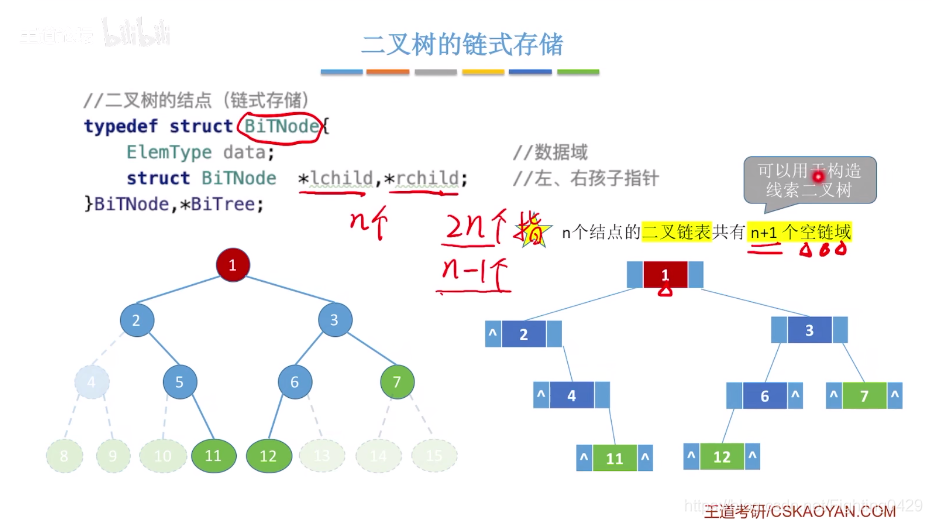
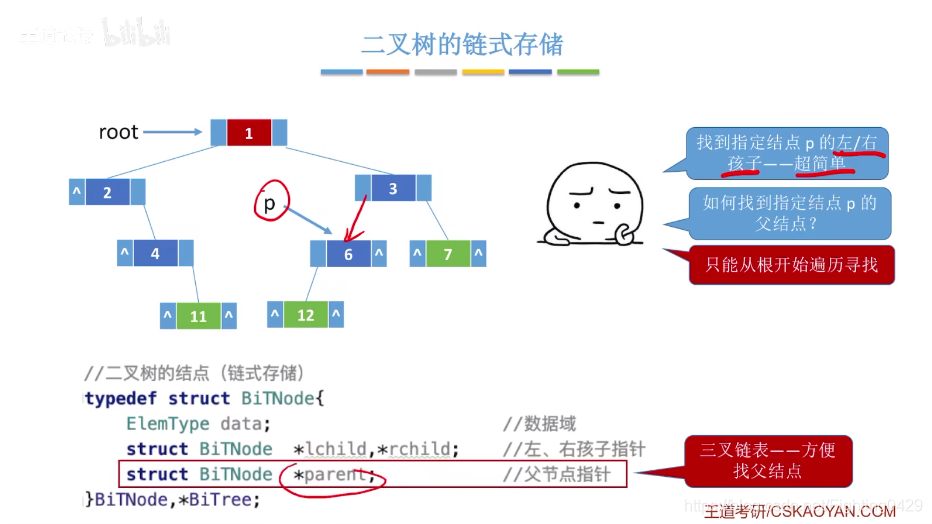
2.2.2、链式存储

2.3、二叉树的遍历

2.3.1、二叉树的先中后序遍历

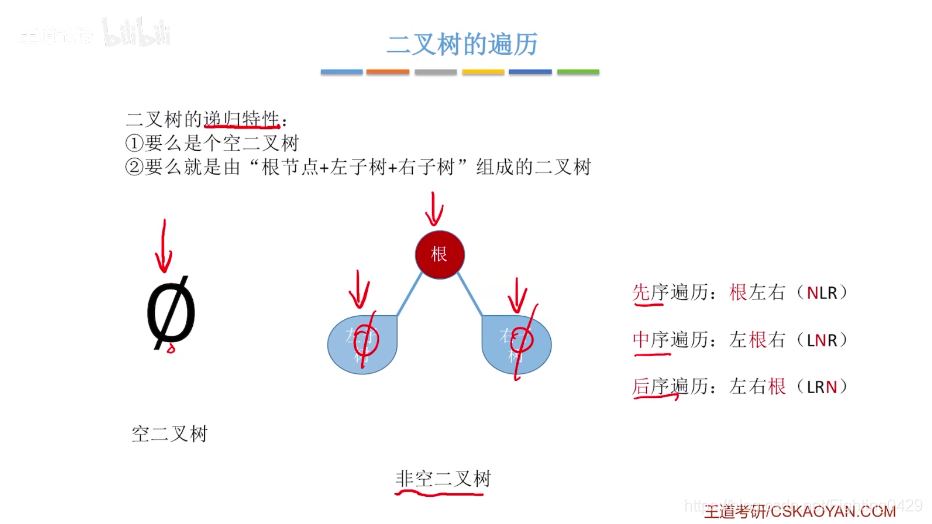
例子：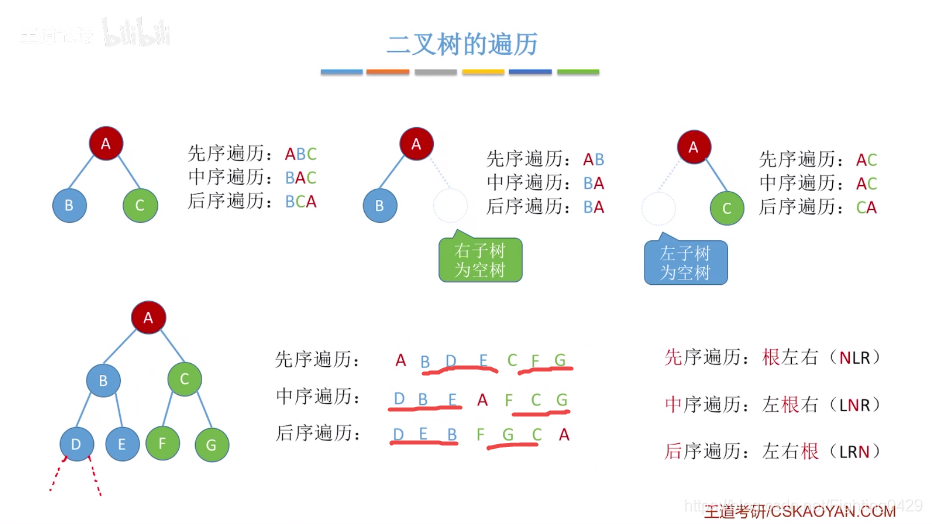

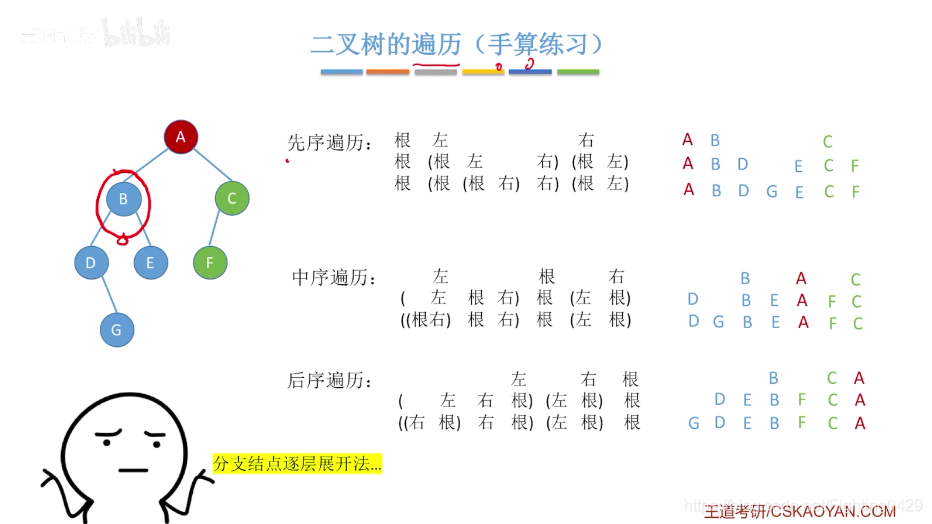
2.3.2、二叉树的层次遍历

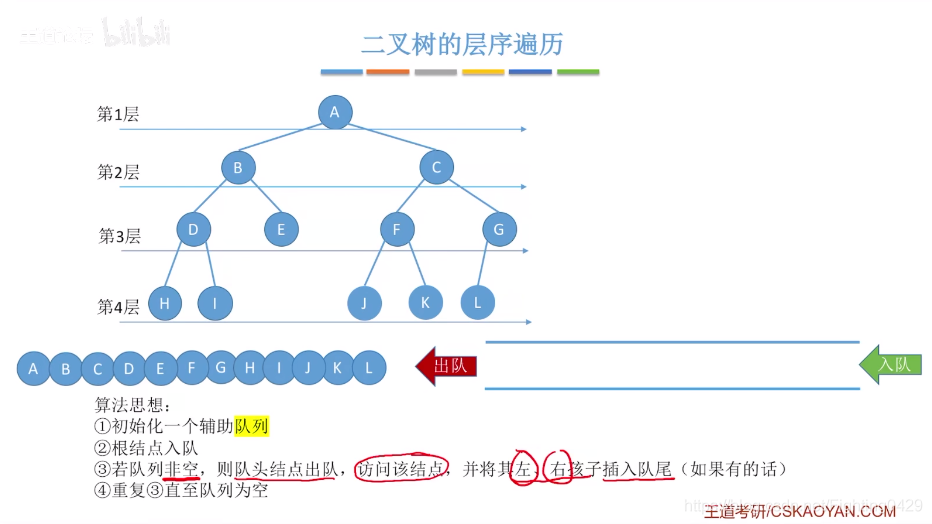
2.3.3、由遍历序列构造二叉树

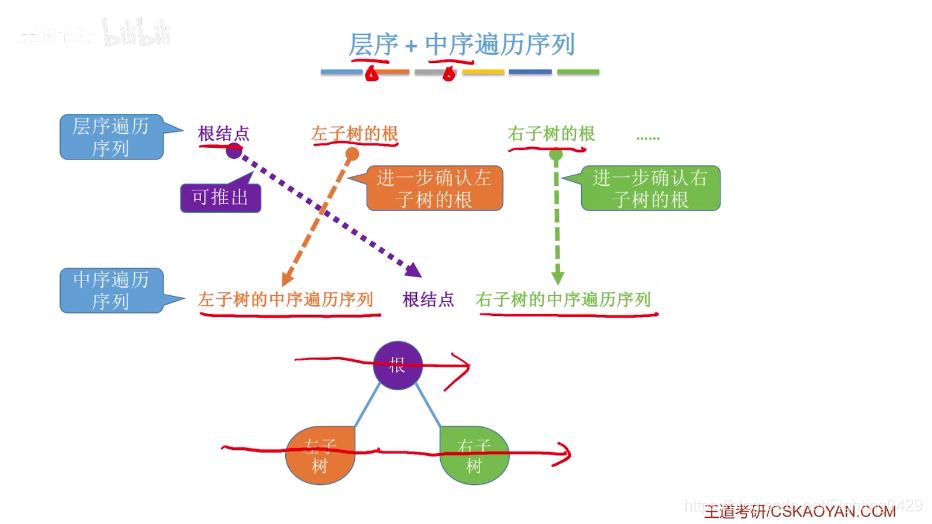
2.3、线索二叉树

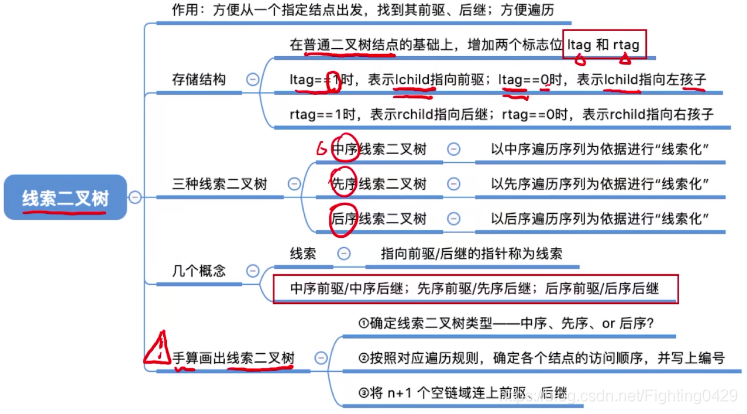
3、树

3.1树的结构

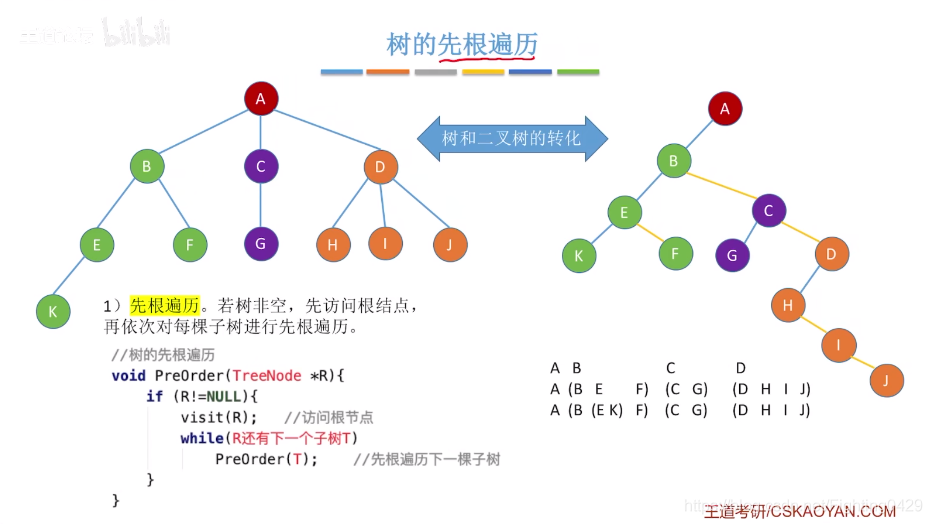
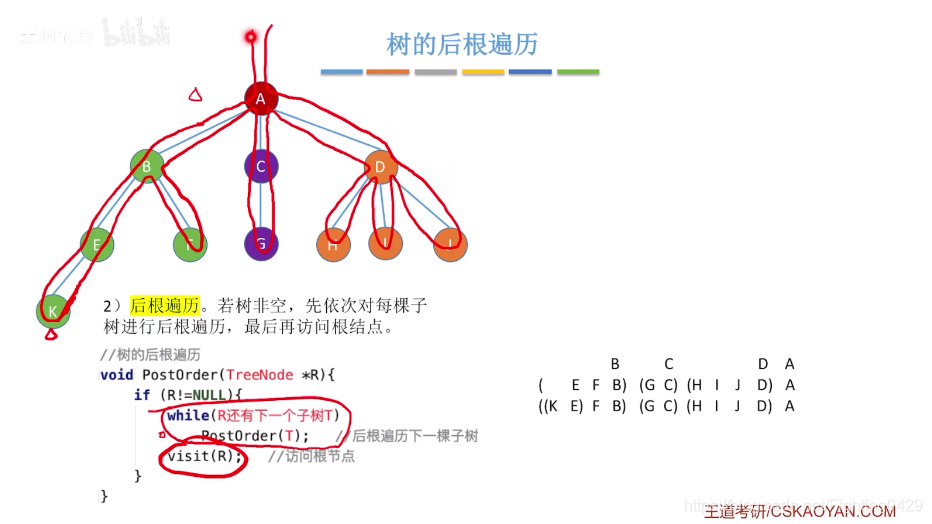
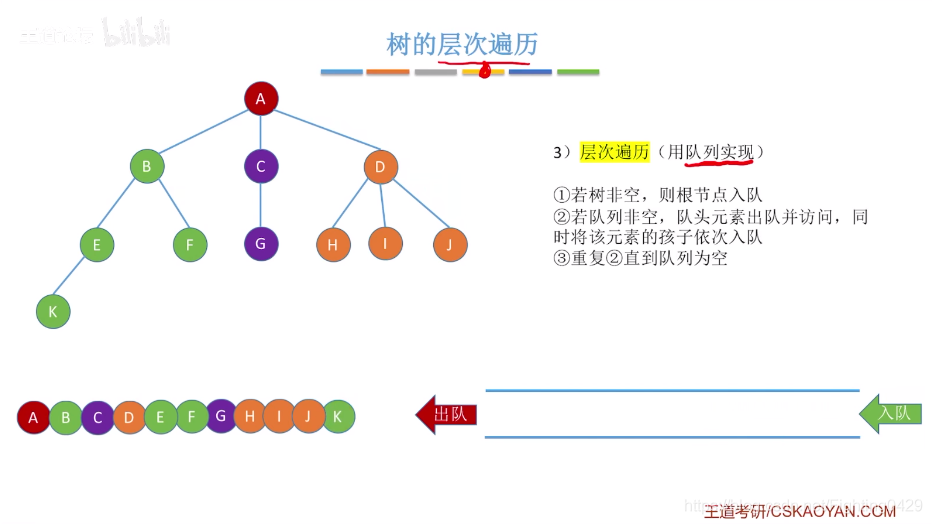
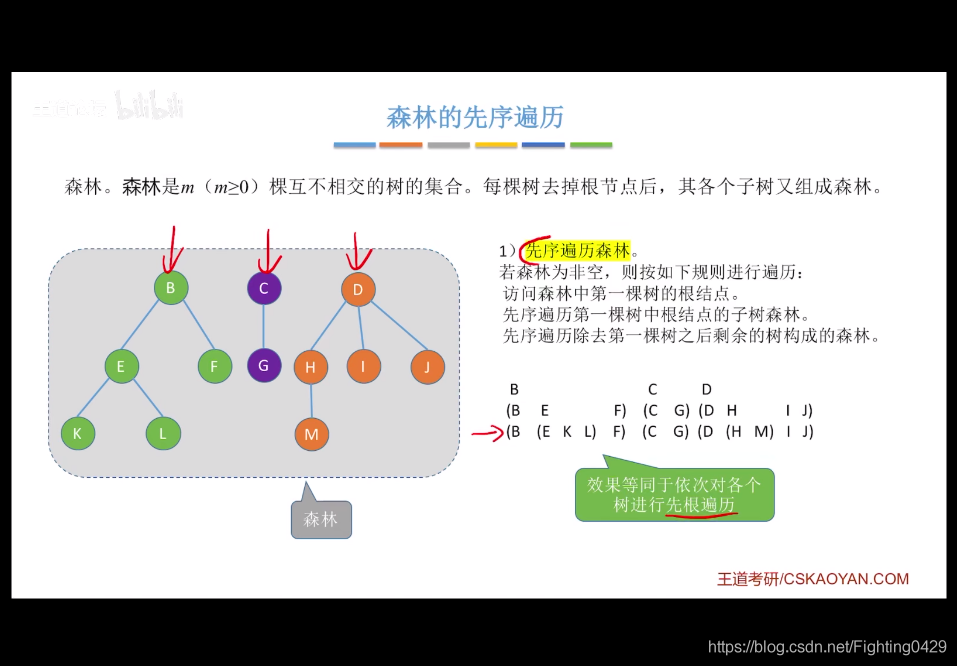
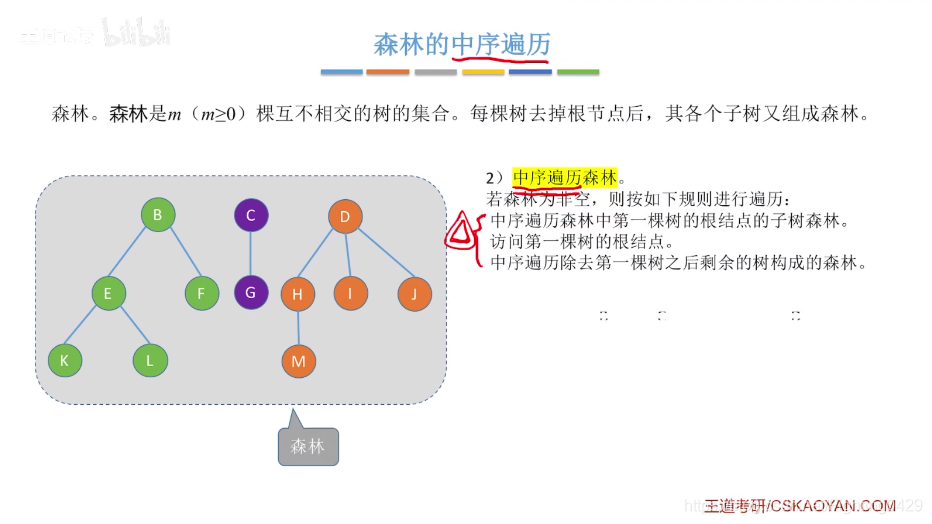
3.2、树和森林的遍历

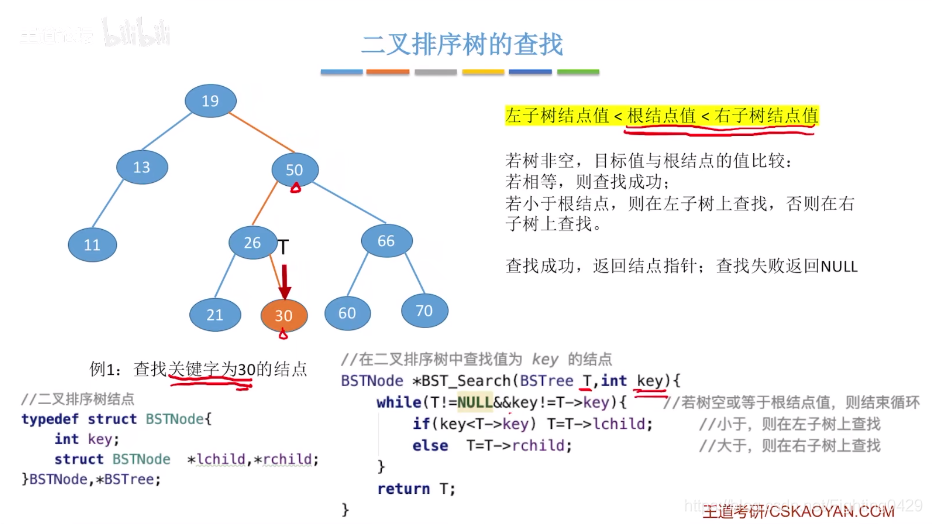
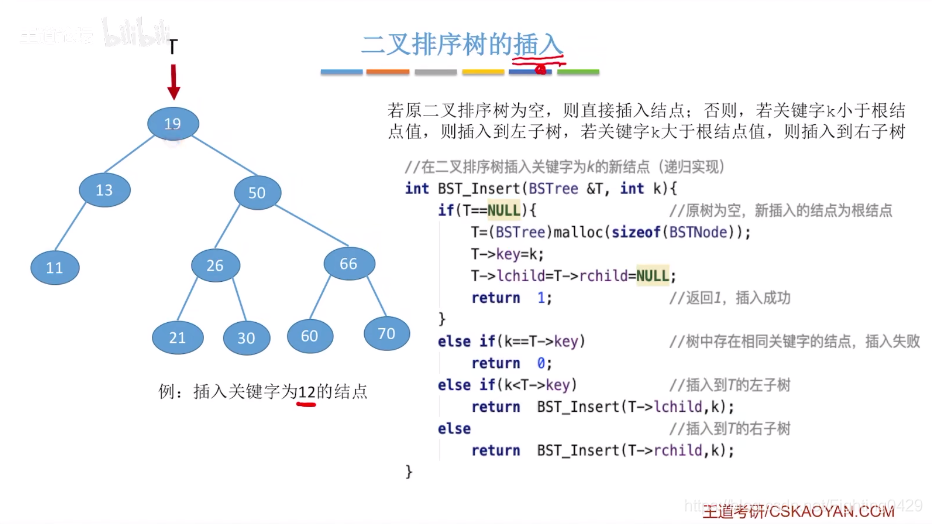
3.2、二叉排序树

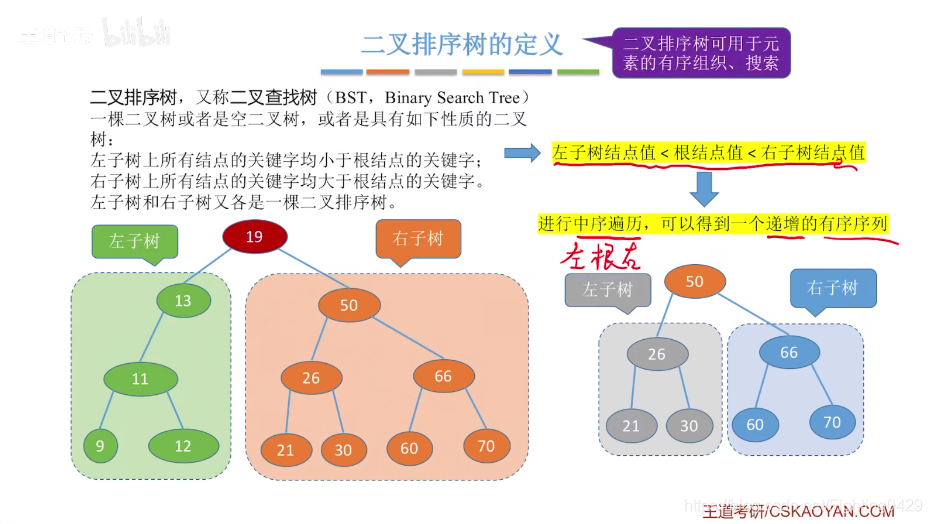
3.3、平衡二叉树

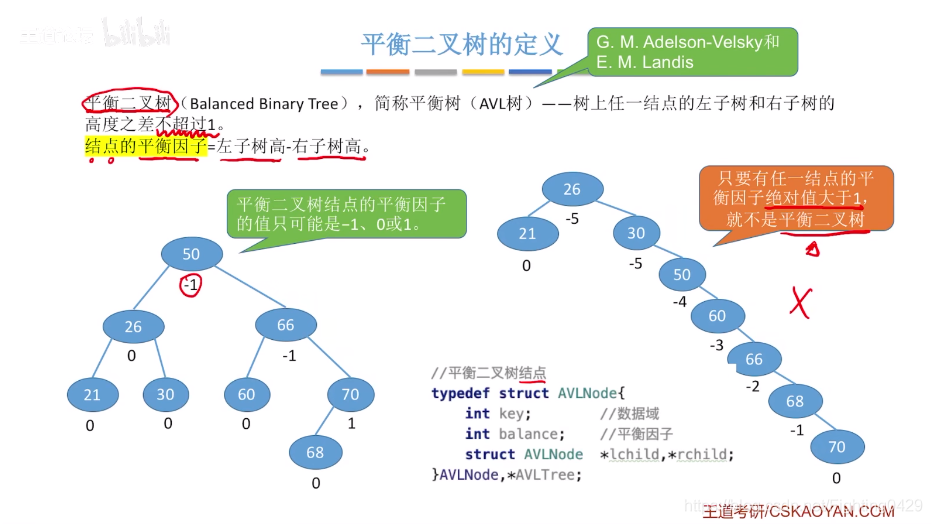
3.3.1、平衡二叉树的定义

3.3.1、调整最小平衡二叉树

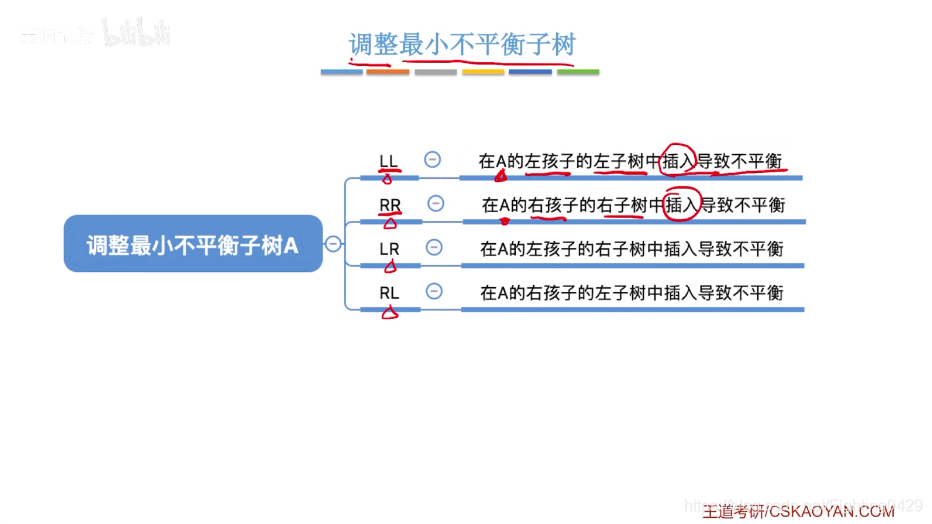
3.4、哈夫曼树

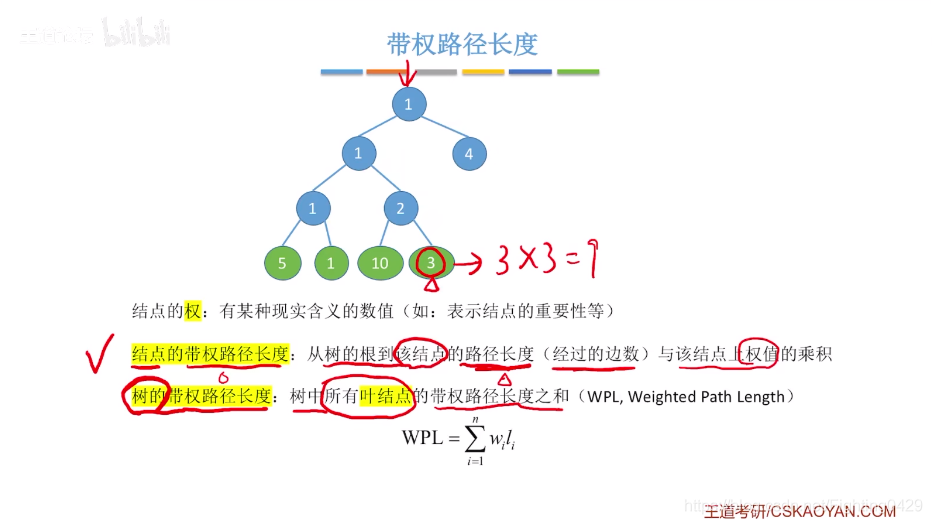
3.4.1、定义

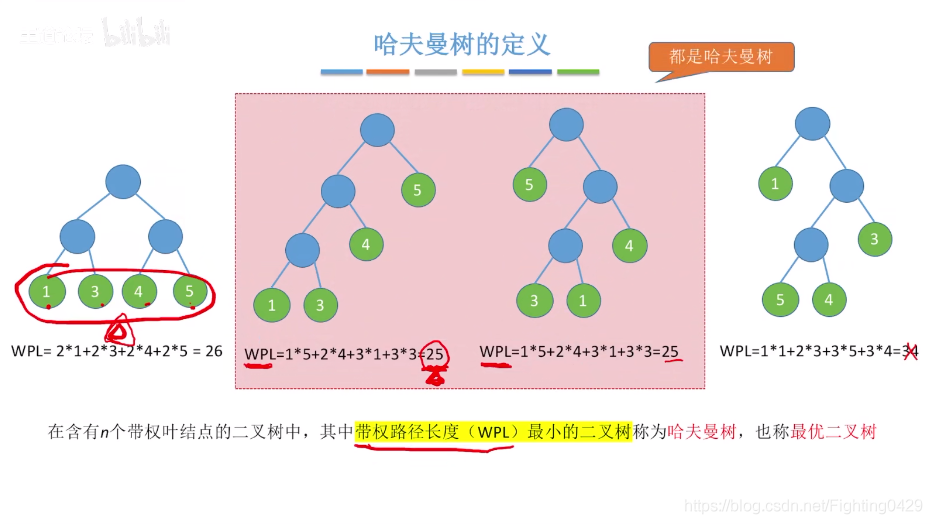
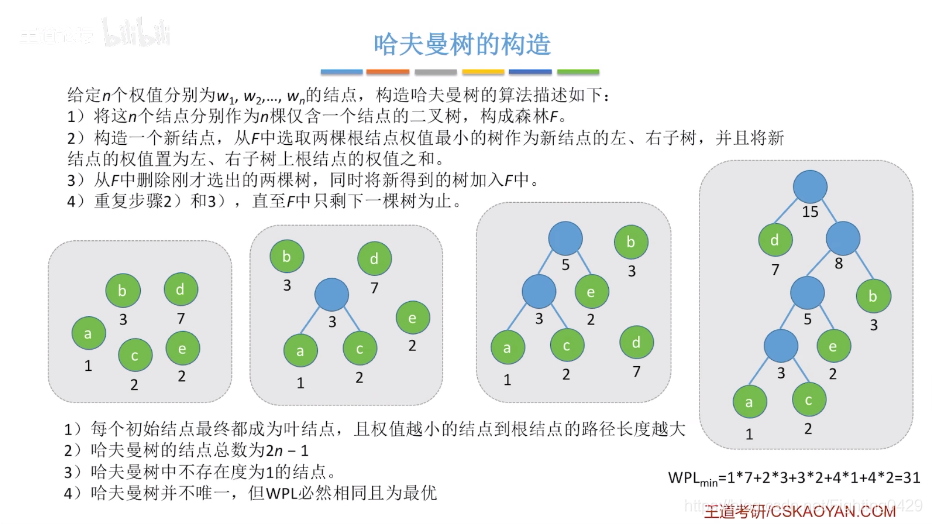
3.4.2、构造

4、python实现树以及遍历

定义一个节点类
class Node:
    """节点类"""
    def __init__(self, elem, left=None, right=None):
        self.elem = elem
        self.left = left
        self.right = right


class Tree:
    """树类"""
    def __init__(self, root=None):
        self.root = root


    # 增加节点
    def add(self,item):
        # 创建一个节点
        node = Node(item)
        if self.root is None:
            self.root = node
            return
        # 用一个队列存放根节点
        queue = [self.root]
        # 循环遍历数
        while queue:
            # 根节点出队列
            cur_node = queue.pop(0)
            # 当该节点没有左子树时，新节点连接到左边
            if not cur_node.left:
                cur_node.left = node
                return
            else:
                # 该节点存在左子树，将该左节点入队列
                queue.append(cur_node.left)
            # 当该节点没有右子树时，新节点连接到右边
            if not cur_node.right:
                cur_node.right = node
                return
            else:
                queue.append(cur_node.right)

    def breadth_trav(self):
        """广度遍历--层次遍历"""
        if self.root is None:
            return
        # 根节点队列
        queue = [self.root]
        # 循环遍历
        while queue:
            # 根节点出队
            cur_node = queue.pop(0)
            # 输出节点值
            print(cur_node.elem,end=" ")
            # 若该节点存在左节点
            if cur_node.left:
                # 将左节点入队
                queue.append(cur_node.left)
            if cur_node.right:
                queue.append(cur_node.right)

    def preorder(self,root):
        """深度先序递归遍历所有节点（递归）"""
        if root is None:
            return

        print(root.elem,end=" ")
        self.preorder(root.left)
        self.preorder(root.right)

    def depth_trav(self):
        """深度---先序遍历（迭代）"""
        if self._root is None:
            return
        # 根节点列表
        queue = [self._root]
        # 循环遍历
        while queue:
            # 取根节点
            cur_node = queue.pop()
            # 输出节点值
            print(cur_node.elem,end=" ")

            if cur_node.right:
                queue.append(cur_node.right)
            # 若该节点存在左节点
            if cur_node.left:
                # 将左节点入队
                queue.append(cur_node.left)

   
    def infix(self,root):
        """深度中序递归遍历所有节点（递归）"""
        if root is None:
            return

        self.infix(root.left)
        print(root.elem,end=" ")
        self.infix(root.right)

   
    def epilogue(self,root):
        """深度后序递归遍历所有节点（递归）"""
        if root is None:
            return

        self.epilogue(root.left)
        self.epilogue(root.right)
        print(root.elem,end=" ")


if __name__ == "__main__":
    tree = Tree()
    tree.add(1)
    tree.add(2)
    tree.add(3)
    tree.add(4)
    tree.add(5)
    tree.add(6)
    tree.add(7)
    tree.add(8)
    tree.breadth_trav()
    print(" ")
    tree.preorder(tree.root)
    print(" ")
    tree.infix(tree.root)
    print(" ")
    tree.epilogue(tree.root)