Softmax激活函数与梯度方向

Softmax函数属于有监督学习的范畴，一般用于多分类问题，在神经网络中应用广泛，很多时候作为输出层的激活函数使用。它可以被理解成升级版的Sigmoid函数，本质上是逻辑回归常用Sigmoid函数一般化，将k维的任意实数映射成k维的向量，Softmax的数值只能从0到1，表示的是分到相对应类别o的概率，因此所有的Softmax值加起来总和等于1。通常我们会选取概率最大的类别作为分类的结果。Softmax的作用在于相对“Hardmax”函数(即常用的max函数)，在任何地方都是连续可导的，这个数学特性在很多机器学习中的梯度下降过程中有着更重要的作用。

Softmax函数表达式如下：

$S_{i}=\frac{e^{y_{i}}}{\sum_{i=1}^{k}e^{y_{k}}}$ ，

其中 $S_{i}$ 为第 $S_{i}$ 个神经元中Softmax函数激活计算出来的值， $S_{i}$ 为为第 $S_{i}$ 个神经元的输出值， $S_{i}$ 表示需要分类类别的数量，如二分类器中， $S_{i}$ 就为2。

现在假设在BP神经网络中，一般形式为：

$S_{i}$ ，其中 $S_{i}$ 为为第 $S_{i}$ 个神经元的输出值，与上式的 $S_{i}$ 对应， $S_{i}$ 为第 $S_{i}$ 个特征的权重， $S_{i}$ 为第 $S_{i}$ 个特征的值。

另外假设损失函数为常用的交叉熵损失函数(Cross Entropy Loss Function)：

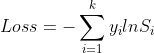$Loss=-\sum_{i=1}^{k}y_{i}lnS_{i}$ ，其中 $S_{i}$ 三者的含义同上。

在梯度下降法中，我们需要对损失函数求偏导，Softmax在这点上相对输出0,1值来说就提供了一个比较平滑的过度，由于假设是在BP神经网络中，因此每个特征的权重 $S_{i}$ 都是随机选择，最终拼凑计算成输出值 $S_{i}$ ，所以我们只需要对输出值 $S_{i}$ 求导就好了，得出的梯度方向就是计算机需要各种拼凑得出的值，我们接下来推导一下这个过程：

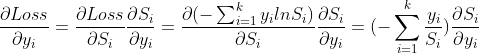$\frac{\partial Loss}{\partial y_{i}}=\frac{\partial Loss}{\partial S_{i}} \frac{\partial S_{i}}{\partial y_{i}}=\frac{\partial (-\sum_{i=1}^{k}y_{i}lnS_{i})}{\partial S_{i}}\frac{\partial S_{i}}{\partial y_{i}}=(-\sum_{i=1}^{k}\frac{y_{i}}{S_{i}})\frac{\partial S_{i}}{\partial y_{i}}$ ，

其中第二部分 $S_{i}$ 需要分情况讨论，分开梯度方向向该分类求导的时候(i=j)和梯度不向该分类求导的时候(i!=j)，

梯度方向向该分类求导的时候(i=j)：

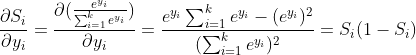
$\frac{\partial S_{i}}{\partial y_{i}}=\frac{\partial (\frac{e^{y_{i}}}{\sum_{i=1}^{k}e^{y_{i}}})}{\partial y_{i}}=\frac{e^{y_{i}}\sum_{i=1}^{k}e^{y_{i}}-(e^{y_{i}})^{2}}{(\sum_{i=1}^{k}e^{y_{i}})^{2}}=S_{i}(1-S_{i})$

梯度不向该分类求导的时候(i!=j)：

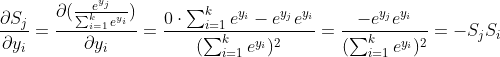
$\frac{\partial S_{j}}{\partial y_{i}}=\frac{\partial (\frac{e^{y_{j}}}{\sum_{i=1}^{k}e^{y_{i}}})}{\partial y_{i}}=\frac{0\cdot \sum_{i=1}^{k}e^{y_{i}}-e^{y_{j}}e^{y_{i}}}{(\sum_{i=1}^{k}e^{y_{i}})^{2}}=\frac{-e^{y_{j}}e^{y_{i}}}{(\sum_{i=1}^{k}e^{y_{i}})^{2}}=-S_{j}S_{i}$

所以合并上述两种情况，这者相加，

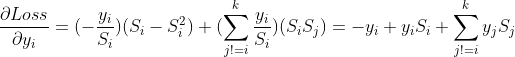
$\frac{\partial Loss}{\partial y_{i}}=(-\frac{y_{i}}{S_{i}})(S_{i}-S^{2}_{i})+(\sum_{j!=i}^{k}\frac{y_{i}}{S_{i}})(S_{i}S_{j})=-y_{i}+y_{i}S_{i}+\sum_{j!=i}^{k}y_{j}S_{j}$

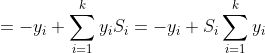
$=-y_{i}+\sum_{i=1}^{k}y_{i}S_{i}=-y_{i}+S_{i}\sum_{i=1}^{k}y_{i}$

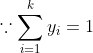
$\because \sum_{i=1}^{k}y_{i}=1$ $S_{i}$ $S_{i}$

我们可以看出，最后，梯度下降的方向只是真实分类的类别方向中基于Softmax函数得出的值减去1

参考文献：

Softmax 函数的特点和作用是什么？ - 忆臻的回答 - 知乎 https://www.zhihu.com/question/23765351/answer/240869755

原文链接：https://blog.csdn.net/joeland209/article/details/82623542