前边的文章介绍过在时域上系统的特征根对系统特性的影响:
二阶系统欠阻尼状态极点位置对阶跃响应的影响
这里简单回顾下:
典型二阶系统的传递函数如下:
H ( s ) = ω n 2 s 2 + 2 ξ ∗ ω n ∗ s + ω n 2 \ H(s)= \frac{ωn^2 }{s^2 +2ξ*ωn*s+ωn^2} H(s)=s2+2ξ∗ωn∗s+ωn2ωn2
特征方程为:
s 2 + 2 ξ ∗ ω n ∗ s + ω n 2 = 0 \ {s^2 +2ξ*ωn*s+ωn^2}=0 s2+2ξ∗ωn∗s+ωn2=0
欠阻尼状态下的特征根为:
s 1 , 2 = − ξ ∗ ω n ± j w n ∗ 1 − ξ 2 ( 0 < ξ < 1 ) \mathop{{s}} \nolimits_{{1,2}} = {-ξ*ωn \pm j wn*\sqrt{1-ξ^2}}(0<ξ<1)s1,2=−ξ∗ωn±jwn∗1−ξ2(0<ξ<1)
特征根的实部决定了系统的稳定时间ts,阻尼系数决定了系统的超调量。
σ = e − π ∗ ξ 1 − ξ 2 t s = 3.5 ξ ∗ ω n ( 包 络 线 正 负 百 分 5 ) \ σ = e^\frac {-π*ξ}{\sqrt{1-ξ^2}}\\ \ ts = \frac {3.5}{ξ*ωn}(包络线正负百分5) σ=e1−ξ2−π∗ξ ts=ξ∗ωn3.5(包络线正负百分5)
本文主要包含以下内容:
一、三段法简介
二、低频段对特性的影响
三、中频段对特性的影响
四、高频段对特性的影响
一、三段法简介
三段法即将系统幅频特性区域分为低频段,中频段,高频段三段,其中,低频段主要看系统的开环增益,决定系统的稳态误差;中频段主要看系统的相位余量以及穿越频率,决定系统的稳定时间以及超调量;高频段要求系统看系统的开环增益,决定系统的高频抗干扰能力。
二、低频段
通常指第一个转折频率左侧的频段,这一段的特性由积分环节和开环增益决定,设低频段对应的传递函数为:
G d ( s ) = K s v \ Gd(s) = \frac {K}{s^v} Gd(s)=svK
从《控制系统稳态误差(静态误差)分析》文章介绍
v决定系统的型别,K决定不同型别下不同响应的稳态误差: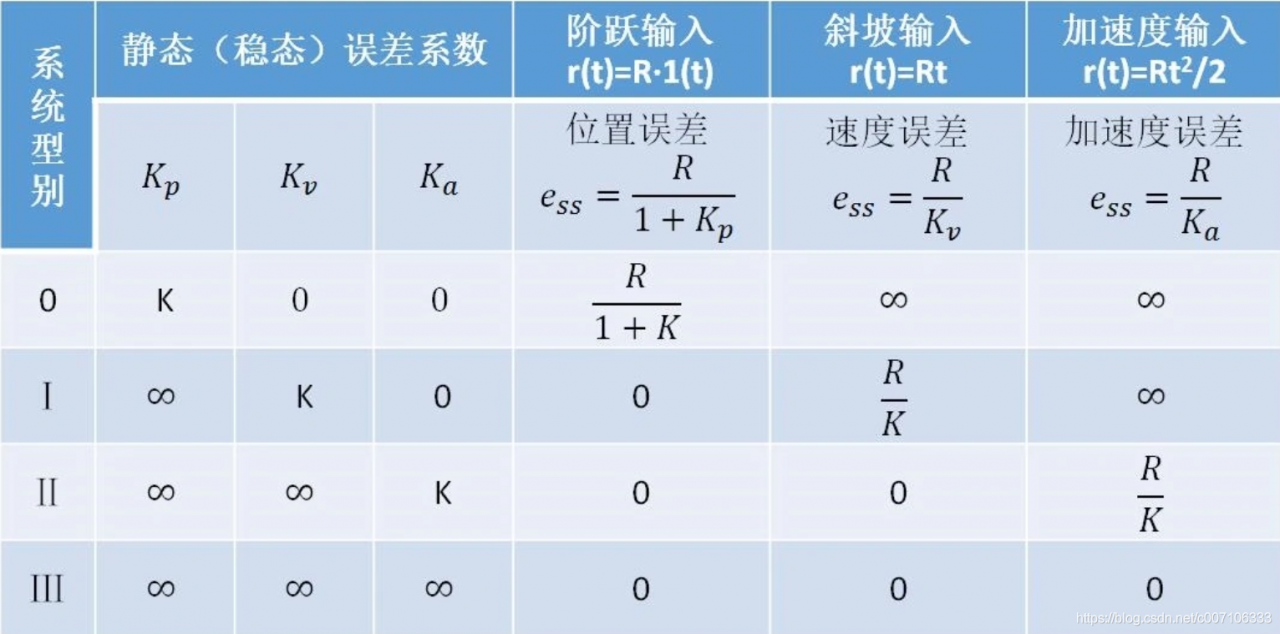
因此在设计系统时,我们需要根据稳态误差要求来确定最小需要的开环增益k.
三、中频段
通常中频段指截止频率附近的频段,相位裕度γ与阻尼系数ξ相关,确定相位余量后,系统的开环截止频率ωc决定了系统的稳定时间ts。
具体而言:
γ = a r c t a n 2 ξ 4 ξ 4 + 1 − 2 ξ 2 \ γ = arctan\frac {2ξ}{\sqrt{\sqrt{4ξ^4+1}-2ξ^2}} γ=arctan4ξ4+1−2ξ22ξ
由此可知ξ越大 γ 越大σ%越小。
t s ω c = 7 t a n γ \ tsωc = \frac {7}{tanγ} tsωc=tanγ7
当确下γ和ts要求时候,可以求出ωc。从公式可以看出,γ一定时候ωc 越大,越小。
四、高频段
高频段原理系统截止频率,对系统动态性能影响很小,但从系统扛干扰能力上来说,高频段增益越低,下降斜率越大,系统抗高频干扰能力越强。
五,高阶系统
从以上分析来看,二阶系统通过幅频特性曲线来分析系统动态性能,没有时域分析来的简单直观,但高阶是系统即使用时域法降阶分析也挺麻烦,当然三阶以上的系统要求出频域的γ和ωc也不容易。因此我们的前人总结了如下经验近似公式,方便估算系统特性:
σ = [ 0.16 + 0.4 ( 1 s i n γ − 1 ) ] ( 35 ° ≤ γ ≤ 90 ° ) t s = p i ω c [ 2 + 1.5 ( 1 s i n γ − 1 ) + 2.5 ( 1 s i n γ − 1 ) 2 ] ( 35 ° ≤ γ ≤ 90 ° ) \ σ = {[0.16+0.4( \frac{1}{sinγ}-1)]} (35°≤γ≤90°)\\ \ ts = \frac {pi}{ωc} [2+1.5(\frac {1}{sinγ}-1)+2.5(\frac {1}{sinγ}-1)^2](35°≤γ≤90°) σ=[0.16+0.4(sinγ1−1)](35°≤γ≤90°) ts=ωcpi[2+1.5(sinγ1−1)+2.5(sinγ1−1)2](35°≤γ≤90°)
当系统ωc一定时,γ增加, σ和ts都会下降。