ⅰ.设计题目:
已知某LIT系统的差分方程为:
3y(n)-4y(n-1)+2y(n-2)=x(n)+2x(n-1)
计算n=[-20:100]时的系统单位冲激响应。
ⅱ.设计要求:
本课程设计应满足以下要求:
1.
实用性:设计的典型函数应该能够正确运行.
2. 可读性:源程序代码清晰,有层次,主要程序段有注释.
ⅲ.设计目的:
在学习了数字信号处理这门课程后,按照基本原理,综合运用所学的知识,利用Matlab
,掌握系统的单位冲激响应内容,由给定的差分方程求解系统的单位冲激响应h(n).
ⅳ.设计原理:
根据给定的差分方程:
3y(n)-4y(n-1)+2y(n-2)=x(n)+2x(n-1)
利用z变换,求出H(z),再通过求其逆变换,得到系统单位冲激响应h(n)。
ⅴ.具体算法:
第一步,根据差分方程:
3y(n)-4y(n-1)+2y(n-2)=x(n)+2x(n-1)
用z变换求出H(z)的表达式,原式可化为:

ⅵ.MATLAB源程序:
计算系统单位冲激响应源程序:
num=[1,2,0];
den=[3,-4,2];
n=[-20:100];
hn=dimpulse(num,den)
hn=dimpulse(num,den);
stem(hn);
title('LTI系统的单位冲激响应')
ⅶ.系统仿真结果:
(1).LTI系统的单位冲激响应的计算结果:
h(n) =
0.3333 1.1111 1.2593
0.9383
0.4115
-0.0768
-0.3768
-0.4512
-0.3504 -0.1664 0.0117 0.1266
0.1609 0.1302
0.0663 0.0016
-0.0421 -0.0571 -0.0482
-0.0261
-0.0027 0.0138
0.0202
0.0177
0.0102
0.0018
-0.0045 -0.0071
-0.0065 -0.0039 -0.0009 0.0014
0.0025 0.0024
LTI系统的单位冲激响应的结果图:
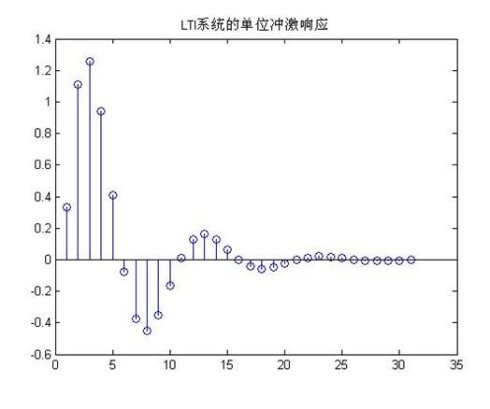
ⅷ.运算结果验证:
在matlab中输入以下程序进行验证:
num=[1,2,0];
den=[3,-4,2];
disp(‘系统传递函数H(z)’);
printsys(num,den,‘z’);
disp(‘转为零极点增益模型’);
[z1,p1,k1]=tf2zp(num,den)
disp(‘转为零极点留数模型’);
[r1,p1]=residue(num,den)
h(n)=dimpulse(num,den)
输出结果为:
系统传递函数H(z)
num/den =
z^2 + 2 z
---------------
3 z^2 - 4 z + 2
转为零极点增益模型
z1 = 0
-2
p1 =0.6667 + 0.4714i
0.6667 - 0.4714i
k1 =0.3333
转为零极点留数模型
r1 =0.5556 - 0.5500i
0.5556 + 0.5500i
p1 =0.6667 + 0.4714i
0.6667 - 0.4714i
h(n)=
0.3333 1.1111 1.2593 0.9383
0.4115
-0.0768
-0.3768 -0.4512
-0.3504 -0.1664 0.0117 0.1266
0.1609 0.1302
0.0663 0.0016
-0.0421 -0.0571 -0.0482 -0.0261
-0.0027 0.0138
0.0202 0.0177
0.0102
0.0018 -0.0045
-0.0071
-0.0065 -0.0039 -0.0009 0.0014
0.0025 0.0024
ⅸ.对其进行理论验证:
当n=0时,
当n=1时,
同理可证,当n=2,3,……时,结果均与源程序运行结果相符,此实践课题已正确完成。
