LeetCode 437. 路径总和 III

【问题描述】

给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的 路径 的数目。

路径 不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

LeetCode 437. 路径总和 III）

【示例1】

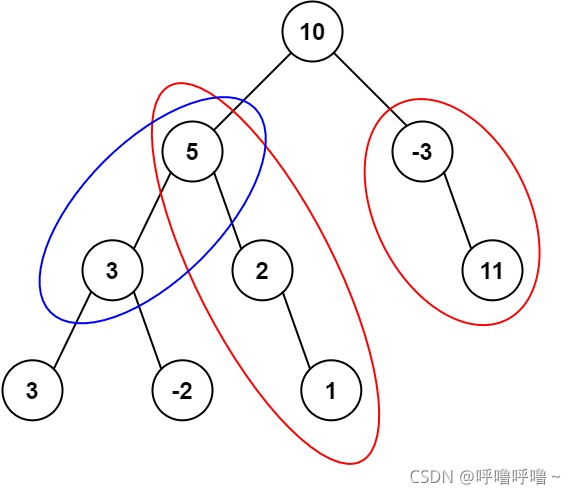
输入：root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
输出：3
解释：和等于 8 的路径有 3 条，如图所示。

【示例2】

输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：3

【数据范围】

二叉树的节点个数的范围是 [0,1000]
-10e9 <= Node.val <= 10e9
-1000 <= targetSum <= 1000

思路：

题目要求的是一段从父节点一直到子节点的连续段的和，有点类似 （一模一样）前缀和，就是在每条路径上进行求前缀和，在答案上加上满足条件条件的个数。
不了解前缀和的uu：
用pre[i]表示前i个数的和，然后用map存储起来，常用于判断连续和
例如：

当我要判断是否有连续段的和为9，当index=5时只需要查询map里面是否有6这个数（这里简单的描述就是pre[i]+targetSum==pre[j]，那么判断是否出现了targetSum，只要判断是否出现了pre[j]-targetSum);这里出现了pre[3]==6所以有【3，5】连续和为9。

那么这题的思路其实是一模一样，但是这里注意要对targetSum==0的情况进行特判，什么？你问我为什么？

以前序遍历为例：当每次遍历到叶子节点时，对根节点到该叶子节点的路径使用
前缀和技巧，添加该路径上的满足连续和为targetSum的数量。
因为本题出现了负值，所以这里对targetSum ==0需要进行判断。
常规的前缀和是可能不取数的，这里不能不取数，所以targetSum ==0时会出现错误，当targetSum ==0时，答案多加的数其实就是元素个数，用计数器统计一下元素个数，结果的时候减去num就行了。

代码示例：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
	int ans=0;
	int num=0;
	void dfs(TreeNode* root,int sum,
		int targetSum,unordered_map<int,int>&mp){
		    if(root==nullptr){//递归终止条件
		         return;
		    }
				    
		    sum+=root->val;
		    mp[sum]++;//添加前缀和
		    
		    num++;//计算元素个数
		    ans+=mp[sum-targetSum];//添加满足题意的连续和组数
				    
		    dfs(root->left,sum,targetSum,mp);//左子树
			dfs(root->right,sum,targetSum,mp);//右子树

             mp[sum]--;//还原状态
	}
    int pathSum(TreeNode* root, int targetSum) {
		unordered_map<int,int>mp;
	    mp[0]=1;//初始化边界
	    dfs(root,0,targetSum,mp);
		if(targetSum==0)//含负数，特判
			return ans-num;
		return ans;
    }
};

【结果】