顺序查找方法和二分查找方法

思考：给定一个已排好序的n个元素a[0:n-1]，如何在n个元素中找到特定的元素x？
此时提供两种方法：

顺序查找法：

顺序搜索法实现原理就是逐个比较a[0:n-1]中的元素，直到找出元素x或搜索遍整个数组后确定x不在其中。

所以，在最后情况下，需要比较O(n)次。可以看出顺序搜索法并没有很好的利用元素已经排序的条件。

二分查找法：

二分搜索法的基本思想是：将n个元素分成个数大致相同的两半，取a[n/2]与x作比较。如果x=a[n/2]，则找到x，算法终止；如果x<a[n/2]，则只在数组a的左半边继续搜索x；如果x>a[n/2]，则只在数组a的右半边继续搜索x。

所以，二分搜索法在最坏情况下需要比较O(log2n）（是以2为底，n的对数）次。

二分查找法的前提就是元素必须是从小到大或从大到小排序的。

语法补充：用在方法的内部，终止本方法的执行或返回数据值给方法的调用者。
难得的尝试写了代码验证一下

package curri;
import java.util.ArrayList;
import java.util.List;
/**
 * 假设有0-100个按照从小到大次序排序的数字，计算找出67需要比较的次数。
 */
public class Select {
	//顺序查找方法
	public int orderSearch(int n){
		List<Integer> list = new ArrayList<Integer>();
		for(int i=1;i<=100;i++){
			list.add(i);
		}
		int m = 0;
		for(int i:list){
			m++;
			if(i==n){
				break;
			}
		}
		return m;
	}
	/**二分查找法*/
	public int bipartiteSelect(int n) {
		List<Integer> list = new ArrayList<Integer>();
		for(int i=1;i<=100;i++){
			list.add(i);
		}
		int m=0,left = 0,right = list.size();
		while(left<=right){
			m++;
			int mid = (left+right)/2;
			if (n==mid) {
				return m;
			}else if(n>mid){
				left = mid+1;
			}else{
				right = mid-1;
			}
		}
		return -1;
	}
	public static void main(String[] args) {
		Select a = new Select();
		System.out.println("顺序法比较次数："+a.orderSearch(67)+"次");
		System.out.println("二分法比较次数为："+a.bipartiteSelect (67)+"次");
	}
}

结果为：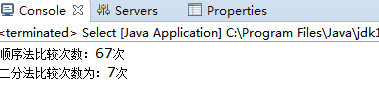

顺序法原理很简单，就不做解释了。
二分查找法的过程，我大致写了一下，

• m=1时，left=0，right=100，此时mid=50,67>mid=50,所以left=mid+1,right=list.size()
• m=2时，left=51，right=100，此时mid=75,67<mid=75,所以left=51,right=mid-1
• m=3时，left=51，right=74，此时mid=62,67>mid=62,所以left=mid+1,right=74
• m=4时，left=63，right=74，此时mid=68,67<mid=68,所以left=63,right=mid-1
• m=5时，left=63，right=67，此时mid=65,67>mid=65,所以left=mid+1,right=67
• m=6时，left=64，right=67，此时mid=66,67>mid=66,所以left=mid+1,right=67
• m=7时，left=67，right=67，此时mid=67,67==mid,结束计算。

两种方法效率很明显，二分查找在数据是排序后的情况下，效率远远高于顺序查找法。