最小二乘法则是一种统计学习优化技术，它的目标是最小化误差平方之和来作为目标，从而找到最优模型，这个模型可以拟合（fit）观察数据。
回归学习最常用的损失函数是平方损失函数，在此情况下，回归问题可以用著名的最小二乘法来解决。最小二乘法就是曲线拟合的一种解决方法。
最小二乘法的问题分为两类：

线性最小二乘法
非线性最小二乘法

如果是线性的则有闭式解(closed-form solution)，唯一解。理解为所有点都在某条线上，全拟合好了。
非线性的经常需要数值方法来求解。比如：随机梯度下降或者牛顿法等。当然，随机梯度下降也可以解决线性问题。

目标公式

J(θ)=∑i=1m(fθ(xi)−yi)2(1)(1)J(θ)=∑i=1m(fθ(xi)−yi)2

最小二乘法的目标就是最小化公式1。f则是模型（取自假设空间），y则是观察值。
通俗来讲，就是观察值和拟合值(模型给出）之间的距离平方和最小化作为目标来优化。

求解方法

矩阵求导方法

思想就是把目标函数划归为矩阵运算问题，然后求导后等于0，从而得到极值。以线性回归问题为例：
求解最小二乘的问题推导为如下：求解变量θθ,满足

(XTX)θ=XTy(2)(2)(XTX)θ=XTy

如果可逆，将得到：

θ=(XTX)−1XTyθ=(XTX)−1XTy

这是利用矩阵得到的最小二乘法的一种解法。
注意这是线性回归的最小二乘法的求解结果，不是其他问题的，其他问题的假设函数有时候很复杂。比如下面的博文对线性回归的推算挺好，但没有说明求导的大前提条件：线性回归，这容易把最小二乘法和最小二乘法的求解混在一起。
http://blog.csdn.net/ACdreamers/article/details/44662633

数值方法随机梯度下降

思路：对参数向量求导，使其梯度为0，然后得到参数变量的迭代更新公式。

θj:=θj−α∗∂J(θ)∂(θj)(3)(3)θj:=θj−α∗∂J(θ)∂(θj)

请参考：http://blog.csdn.net/iterate7/article/details/76709492

数值方法牛顿法

利用泰勒公式展开，利用梯度和海塞矩阵进行迭代下降。速度很快。

xk+1=xk−H−1kgk(4)(4)xk+1=xk−Hk−1gk

变量以牛顿方法来下降。
牛顿方向定义为：

−H−1kgk−Hk−1gk

请参考：

http://blog.csdn.net/iterate7/article/details/78387326

最小二乘和梯度下降区别

最小二乘看做是优化问题的话，那么梯度下降是求解方法的一种。梯度下降是一种解决最优化问题的数值方法。最小二乘法则是一个最优化问题。

简单总结

数值方法的基本含义则是对一个函数求极值，在无法直接求得解析解的情况下，通过求导为0的方法，找到迭代方向保证可以下降目标值，梯度方向或者牛顿方向等等。逐步下降直到满足一些工程要求则结束迭代。

后记

最小二乘法是一种对于偏差程度的评估准则思想，由公式1给出。个人认为，应该称之为：最小二乘准则。
公式1里没有给出f的值，也就是说假设空间。如果是线性回归，也就是wx+b的形式，那么公式2就是最小二乘法的解。所以大部分的博文都在此范畴讨论。为何都用这个线性回归直接说呢，其实最小二乘准则更适合线性回归。应该称之为狭义的最小二乘方法，是线性假设下的一种有闭式解的参数求解方法，最终结果为全局最优。
梯度下降只是数值求解的具体操作，和最小二乘准则下面的最优化问题都可以用随机梯度下降求解。

线性回归python

<span style="color:#000000"><code class="language-python"><span style="color:#000088">import</span> numpy <span style="color:#000088">as</span> np
<span style="color:#000088">import</span> matplotlib.pyplot <span style="color:#000088">as</span> plt
data = np.array([
    [<span style="color:#006666">1</span>, <span style="color:#006666">6</span>],
    [<span style="color:#006666">2</span>, <span style="color:#006666">5</span>],
    [<span style="color:#006666">3</span>, <span style="color:#006666">7</span>],
    [<span style="color:#006666">4</span>, <span style="color:#006666">10</span>]
])
m = len(data)
X = np.array([np.ones(m), data[:, <span style="color:#006666">0</span>]]).T
print(<span style="color:#009900">"X:"</span>, X)
y = np.array(data[:, <span style="color:#006666">1</span>]).reshape(-<span style="color:#006666">1</span>, <span style="color:#006666">1</span>)
print(<span style="color:#009900">"y:"</span>,y)
W = np.linalg.solve(X.T.dot(X), X.T.dot(y)) <span style="color:#880000">## 求解XW=y的值，W</span>
print(<span style="color:#009900">"W:"</span>,W)

<span style="color:#880000">##show</span>
plt.figure(<span style="color:#006666">1</span>)
xx = np.linspace(<span style="color:#006666">0</span>, <span style="color:#006666">5</span>, <span style="color:#006666">2</span>)
yy = np.array(W[<span style="color:#006666">0</span>] + W[<span style="color:#006666">1</span>] * xx)
plt.plot(xx, yy.T, color=<span style="color:#009900">'b'</span>)
plt.scatter(data[:, <span style="color:#006666">0</span>], data[:, <span style="color:#006666">1</span>], color=<span style="color:#009900">'r'</span>)
plt.show()</code></span>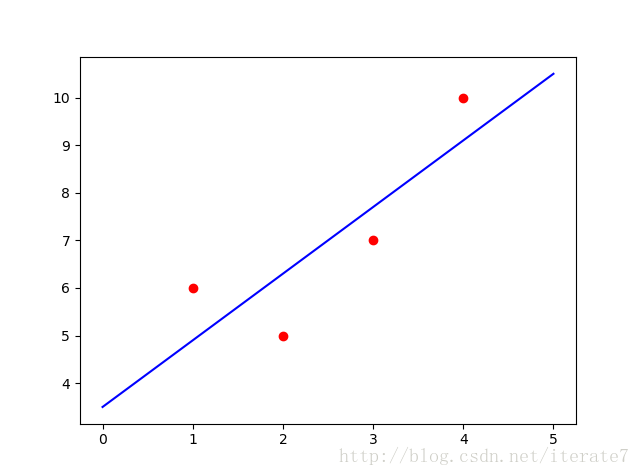

这里写图片描述

参考：
机器学习周志华线性模型和最小二乘法
https://en.wikipedia.org/wiki/Least_squares
https://en.wikipedia.org/wiki/Linear_least_squares_(mathematics)
https://en.wikipedia.org/wiki/Newton‘s_method_in_optimization

原文链接：https://blog.csdn.net/airufengye/article/details/81319089