
思路:
如何从底向上遍历?
遍历整棵树,还是遍历局部树?
如何把结果传到根节点的?
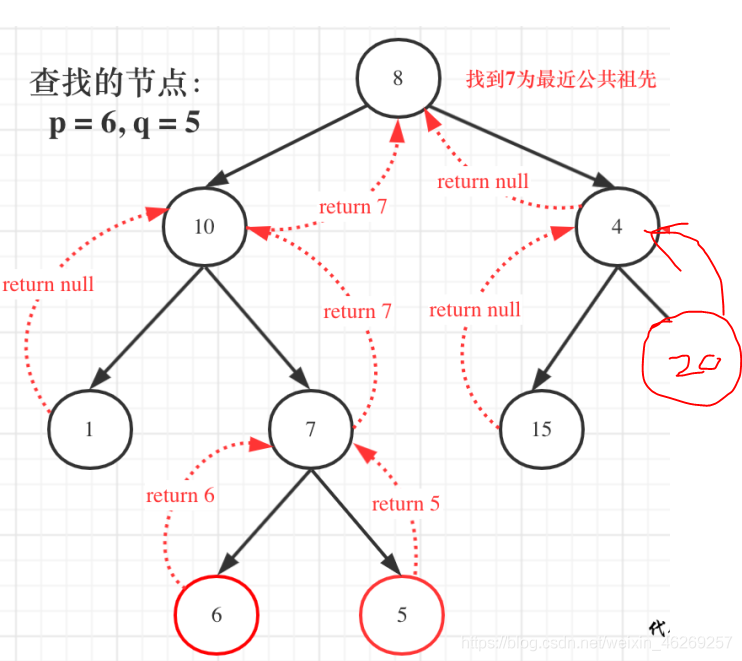
1、利用回溯实现自底向上搜索,查找最近公共祖先。
后序遍历就是一个回溯过程,最先处理的节点一定是叶子节点。
2、怎样判断节点p和节点q的最近公共祖先呢?
(1)、某个节点是节点p和节点q的公共祖先:如果找到一个节点,发现左子树出现节点p,右子树出现节点q。或者左子树出现节点q,右子树出现节点p,则该节点就是节点p和节点q的最近公共祖先。
(2)节点p或节点q是节点p和节点q的公共祖先:某一个节点左/右子树出现p/q,右/左子树为空
递归法
1、确定递归函数的参数和返回值:
需要递归函数的返回值来告诉我们是否找到了节点p和节点q,那么返回值类型理应是bool型。
但是我们如果找到了最近公共祖先,还要返回最近公共祖先这个节点。
怎么办呢,那就利用题目所给的TreeNode* ,如果遇到了p或者q,就把p或者q返回,代表找到了(true)。如果没遇到就返回空,代表没找到(false)
TreeNode* lowestCommonAncestor(TreeNode* root,TreeNode* p,TreeNode* q);
2、确定终止条件
如果找到了节点p或者q,或者遇到了空节点,就返回
if(root==p||root==q||root==NULL) return NULL;
3、确定单层递归的逻辑
TreeNode* left = lowestCommonAncestor(root->left, p, q);
TreeNode* right = lowestCommonAncestor(root->right, p, q);
if (left == NULL && right != NULL) return right;
else if (left != NULL && right == NULL) return left;
else { // (left == NULL && right == NULL)
return NULL;
}
完整递归代码
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if (root == q || root == p || root == NULL) return root;
TreeNode* left = lowestCommonAncestor(root->left, p, q);
TreeNode* right = lowestCommonAncestor(root->right, p, q);
if (left != NULL && right != NULL) return root; //1
if (left == NULL && right != NULL) return right;//2
else if (left != NULL && right == NULL) return left;//3,左边不为空,右边为空,如果先遇到p,说明q一定在p下面,两者公共祖先一定是先遇到的那个。
else { // (left == NULL && right == NULL)
return NULL;//4
}
}
};
总结
1、首先求最近公共祖先,需要从底向上遍历,那么⼆叉树,只能通过后序遍历(即:回溯)实现从底向上的遍历⽅式。
2、然后,我们要根据节点是否是公共祖先的评判标准 ,也就是如果找到⼀个节点,发现左⼦树出现结点p,右⼦树出现节点q,或者 左⼦树出现结点q,右⼦树出现节点p,那么该节点就是节点p和q的最近公共祖先,得出递归函数必须要有返回值用来判断节点左右子树情况,返回最近公共节点。
一般我们会想既然递归函数有返回值,则是单边搜索,于是就用了1的用法
但我们发现了在这种情况是无法完成任务的,因为存在两种情况使我们无法判断要返回哪个节点,即左右子树都不为空和左右子树有一个为空。
所以我们想出了用法2,即全树搜索,总的来看是对返回值根据不同场合进行了不同的处理。
1、
if (递归函数(root->left)) return ;
if (递归函数(root->right)) return ;
2、
left = 递归函数(root->left);
right = 递归函数(root->right);
left与right的逻辑处理;
3、所以在回溯的过程中,必然要遍历整棵⼆叉树,即使已经找到结果了,依然要把其他节点遍历完,因为要使⽤递归函数的返回值(也就是代码中的left和right)做逻辑判断。
4、 要理解如果返回值left为空, right不为空为什么要返回right,为什么可以⽤返回right传给上⼀层结果。
(1)如果当前节点是p或q,则返回p或q,为特殊情况之一,在终止条件得到解决。
(2)当前节点左子树p/q,右子树q/p,为一般情况,在单层处理逻辑中解决。
(3)当前节点左子树为空,右子树为q/p,或者左子树为q/p,右子树为空,为特殊情况之二,也在单层处理逻辑中解决。