目录
为什么要有跳表
目前经常使用的平衡数据结构有:B树,红黑树,AVL树,Splay Tree, Treep等。
想象一下,给你一张草稿纸,一只笔,一个编辑器,你能立即实现一颗红黑树,或者AVL树
出来吗? 很难吧,这需要时间,要考虑很多细节,要参考一堆算法与数据结构之类的树,
还要参考网上的代码,相当麻烦。
用跳表吧,跳表是一种随机化的数据结构,目前开源软件 Redis 和 LevelDB 都有用到它,
它的效率和红黑树以及 AVL 树不相上下,但跳表的原理相当简单,只要你能熟练操作链表,
就能轻松实现一个 SkipList。
搜索:从链表到跳表
我们知道,普通单链表查询一个元素的时间复杂度为O(n),即使该单链表是有序的,我们也不能通过2分的方式缩减时间复杂度。

如上图,我们要查询元素为55的结点,必须从头结点,循环遍历到最后一个节点,不算-INF(负无穷)一共查询8次。那么用什么办法能够用更少的次数访问55呢?最直观的,当然是新开辟一条捷径去访问55。
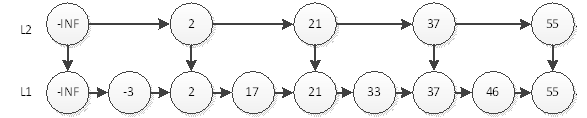
如上图,我们要查询元素为55的结点,只需要在L2层查找4次即可。在这个结构中,查询结点为46的元素将耗费最多的查询次数5次。即先在L2查询46,查询4次后找到元素55,因为链表是有序的,46一定在55的左边,所以L2层没有元素46。然后我们退回到元素37,到它的下一层即L1层继续搜索46。非常幸运,我们只需要再查询1次就能找到46。这样一共耗费5次查询。
那么,如何才能更快的搜寻55呢?有了上面的经验,我们就很容易想到,再开辟一条捷径。
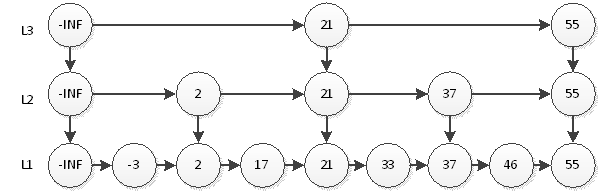
如上图,我们搜索55只需要2次查找即可。这个结构中,查询元素46仍然是最耗时的,需要查询5次。即首先在L3层查找2次,然后在L2层查找2次,最后在L1层查找1次,共5次。很显然,这种思想和2分非常相似,那么我们最后的结构图就应该如下图。
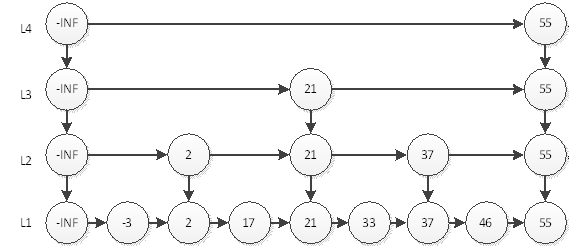
我们可以看到,最耗时的访问46需要6次查询。即L4访问55,L3访问21、55,L2访问37、55,L1访问46。我们直觉上认为,这样的结构会让查询有序链表的某个元素更快。那么究竟算法复杂度是多少呢?
如果有n个元素,因为是2分,所以层数就应该是log n层 (本文所有log都是以2为底),再加上自身的1层。以上图为例,如果是4个元素,那么分层为L3和L4,再加上本身的L2,一共3层;如果是8个元素,那么就是3+1层。最耗时间的查询自然是访问所有层数,耗时logn+logn,即2logn。为什么是2倍的logn呢?我们以上图中的46为例,查询到46要访问所有的分层,每个分层都要访问2个元素,中间元素和最后一个元素。所以时间复杂度为O(logn)。
至此为止,我们引入了最理想的跳跃表,但是如果想要在上图中插入或者删除一个元素呢?比如我们要插入一个元素22、23、24……,自然在L1层,我们将这些元素插入在元素21后,那么L2层,L3层呢?我们是不是要考虑插入后怎样调整连接,才能维持这个理想的跳跃表结构。我们知道,平衡二叉树的调整是一件令人头痛的事情,左旋右旋左右旋……一般人还真记不住,而调整一个理想的跳跃表将是一个比调整平衡二叉树还复杂的操作。幸运的是,我们并不需要通过复杂的操作调整连接来维护这样完美的跳跃表。有一种基于概率统计的插入算法,也能得到时间复杂度为O(logn)的查询效率,这种跳跃表才是我们真正要实现的。
跳表简介
简单说跳表(SkipList)是一种可以替代平衡树的数据结构。跳跃表让已排序的数据分布在多层次的链表结构中,默认是将Key值升序排列的,以 0-1 的随机值决定一个数据是否能够攀升到高层次的链表中。它通过容许一定的数据冗余,达到 “以空间换时间” 的目的。
跳跃表的效率和AVL相媲美,查找/添加/插入/删除操作都能够在O(LogN)的复杂度内完成。
跳表具有如下性质:
(1) 由很多层结构组成
(2) 每一层都是一个有序的链表
(3) 最底层(Level 1)的链表包含所有元素
(4) 如果一个元素出现在 Level i 的链表中,则它在 Level i 之下的链表也都会出现。
(5) 每个节点包含两个指针,一个指向同一链表中的下一个元素,一个指向下面一层的元素。
跳表的实现
java实现参考了 https://blog.csdn.net/fly_yuge/article/details/82755393
节点类
这里的节点类有点像HashMap里的entry,有key和value,如果只想排序的话,可以put的时候value为null(从treemap到treeset)
package datastructure.link.skiplist;
public class Node<T> {
/**
* 在跳表中排序的关键字
*/
public int key;
/**
* 在跳表中存储的值,每个key对应一个value(也可以不放value,这样就相当于从treemap变成treeset)
* 注意:在跳表中,只有最底层的node才有真正的value,其它层的node的value都为null,查找时会到最底层得到value
*/
public T value;
/**
* 左右节点
*/
public Node<T> pre,next;
/**上下节点
*
*/
public Node<T> up,down;
/**
* 头结点被设置成int的min
*/
public static int HEAD_KEY=Integer.MIN_VALUE;
/**尾节点被设置成int的max
*
*/
public static int TAIL_KEY=Integer.MAX_VALUE;
/**Node的构造函数
* @param key 在跳表中排序的关键字
* @param value 在跳表中存储的值,每个key对应一个value
*/
public Node(int key, T value) {
this.key = key;
this.value = value;
}
public int getKey() {
return key;
}
public void setKey(int key) {
this.key = key;
}
public T getValue() {
return value;
}
public void setValue(T value) {
this.value = value;
}
@Override
public String toString() {
return "Node [key=" + key + ", value=" + value + "]";
}
}
跳表的结构
public class SkipList<T> {
/**
* 跳表的头尾
*/
public Node<T> head,tail;
/**
* 跳表所含的关键字的个数
*/
public int size;
/**跳表的层数
*
*/
public int level;
/**随机数发生器
*
*/
public Random random;
/**
* 向上一层的概率
*/
public static final double PROBABILITY=0.5;
/**
* 跳表的构造函数
*/
public SkipList(){
//初始化头尾节点及两者的关系
head=new Node<>(Node.HEAD_KEY, null);
tail=new Node<>(Node.TAIL_KEY, null);
head.next=tail;
tail.pre=head;
//初始化大小,层,随机
size=0;
level=0;
random=new Random();
}搜索
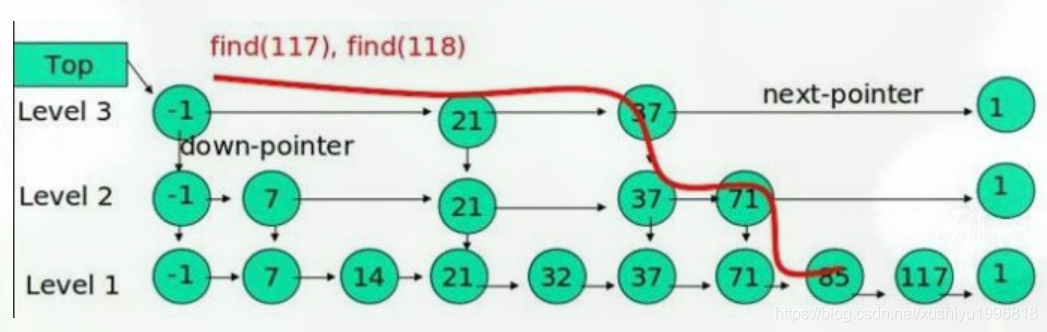
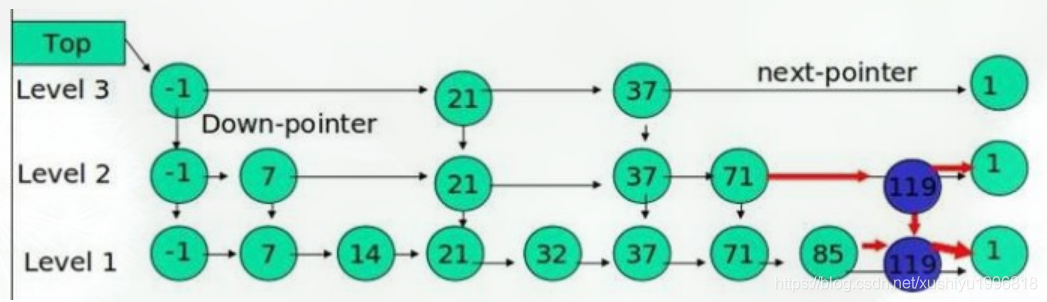
例子:查找元素 117
(1) 比较 21, 比 21 大,往后面找
(2) 比较 37, 比 37大,比链表最大值小,从 37 的下面一层开始找
(3) 比较 71, 比 71 大,比链表最大值小,从 71 的下面一层开始找
(4) 比较 85, 比 85 大,从后面找
(5) 比较 117, 等于 117, 找到了节点。
这里就是先找到最底层最接近key的node(因为这个方法,待会put的时候还要用),然后根据这个node的key,选择返回node或者返回null
/**根据key,返回最底层对应的node,如果不存在这个key,则返回null
* @param key
* @return
*/
public Node<T> get(int key){
//返回跳表最底层中,最接近这个key的node
Node<T> p=findNearestNode(key);
//如果key相同,返回这个node
if(p.key==key){
return p;
}
//如果不相同,返回null
return null;
}
/**返回跳表最底层中,最接近这个key的node<br>
* 如果跳表中有这个key,则返回最底层中,对应这个key的node<br>
* 如果没有这个key,则返回最底层中,小于这个key,并且最接近这个key的node
* @param key
* @return
*/
private Node<T> findNearestNode(int key){
Node<T> p=head;
Node<T> next;
Node<T> down;
while (true) {
next=p.next;
//p先前进到这一层中(一开始在最顶层),p的next>key的位置,然后再考虑向下
if(next!=null&&next.key<=key){
p=next;
continue;
}
down=p.down;
//走到这一步,p在这一层已经无法前进了,就下降一层,在那层进入循环,再往前走
if(down!=null){
p=down;
continue;
}
//到这里,说明已经无法再向下(已经到最底层),无法再向前(当前的p<=key,next>key),最接近key,跳出循环
break;
}
return p;
}插入
插入,现在最底层插入,然后根据概率,向上建立镜像节点(有可能插入n层的概率为0.5^n)
相当与做一次丢硬币的实验,如果遇到正面,继续丢,遇到反面,则停止,
用实验中丢硬币的次数 K 作为元素占有的层数。显然随机变量 K 满足参数为 p = 1/2 的几何分布,
K 的期望值 E[K] = 1/p = 2. 就是说,各个元素的层数,期望值是 2 层。
/**1. 如果put的key,在跳表中不存在,则在跳表中加入,并由random产生的随机数决定生成几层,返回一个null
* 2. 如果put的key存在,则在跳表中对应的node修改它的value,并返回过去的value
* @param key
* @param value
* @return
*/
public T put(int key,T value){
//首先得到跳表最底层中,最接近这个key的node
Node<T> p=findNearestNode(key);
if(p.key==key){
//如果跳表中有这个key,则返回最底层中,对应这个key的node
//在跳表中,只有最底层的node才有真正的value,只需修改最底层的value就行了
T old=p.value;
p.value=value;
return old;
}
//如果跳表中,没有这个key,那么p就是最底层中,小于这个key,并且最接近这个key的node
//q为新建的最底层的node
Node<T> q=new Node<>(key, value);
//在最底层,p的后面插入q
insertNodeHorizontally(p, q);
//当前level(要与总层数Level进行比较)
int currentLevel=0;
//PROBABILITY为进入下一层的可能性,nextDouble()返回[0,1)
//小于PROBABILITY,说明可能性到达(比如说假设为0.7,小于它的概率就是0.7),进入循环,加入上层节点
while (random.nextDouble()<PROBABILITY) {
//最底层为0,到这里currentlevel为当前指针所在的层,被插入的镜像变量在currentlevel+1层
//所以currentLevel=level时,要在level+1层插入,就要加入一层
if(currentLevel>=level){
addEmptyLevel();
}
//找到q的左边(也就是<=p)第一个能够up的节点,并上浮,赋予p
while (p.up==null) {
p=p.pre;
}
p=p.up;
//创建q的镜像变量z,只有key,没有value,插入在现在的p的后面
Node<T> z=new Node<>(key, null);
insertNodeHorizontally(p, z);
//设置z与q的上下关系
z.down=q;
q.up=z;
//指针上浮
q=z;
currentLevel++;
}
//插入完毕后,size扩大,返回null
size++;
return null;
}
/**返回跳表最底层中,最接近这个key的node<br>
* 如果跳表中有这个key,则返回最底层中,对应这个key的node<br>
* 如果没有这个key,则返回最底层中,小于这个key,并且最接近这个key的node
* @param key
* @return
*/
private Node<T> findNearestNode(int key){
Node<T> p=head;
Node<T> next;
Node<T> down;
while (true) {
next=p.next;
//p先前进到这一层中(一开始在最顶层),p的next>key的位置,然后再考虑向下
if(next!=null&&next.key<=key){
p=next;
continue;
}
down=p.down;
//走到这一步,p在这一层已经无法前进了,就下降一层,在那层进入循环,再往前走
if(down!=null){
p=down;
continue;
}
//到这里,说明已经无法再向下(已经到最底层),无法再向前(当前的p<=key,next>key),最接近key,跳出循环
break;
}
return p;
}
/** 在同一层,水平地,在pre的后面,插入节点now
* @param pre 插入节点前面的节点,应该pre.key小于now.key小于pre.next.key
* @param now 插入的节点
*/
private void insertNodeHorizontally(Node<T> pre,Node<T> now){
//先考虑now
now.next=pre.next;
now.pre=pre;
//再考虑pre的next节点
pre.next.pre=now;
//最后考虑pre
pre.next=now;
}
/**
* 在现在的最顶层之上新加一层,并更新head和tail为新加的一层的head和tail,然后更新总level数(字段level)
*/
private void addEmptyLevel(){
Node<T> p1=new Node<T>(Node.HEAD_KEY, null);
Node<T> p2=new Node<T>(Node.TAIL_KEY, null);
//设置p1的下右
p1.next = p2;
p1.down = head;
//设置p2的下左
p2.pre = p1;
p2.down = tail;
//设置之前头尾的上
head.up = p1;
tail.up = p2;
//设置现在的头尾
head=p1;
tail=p2;
//更新level
level++;
}删除
/**在跳表中删除这个key对应的所有节点(包括底层节点和镜像节点)<br>
* 如果确实有这个key,返回这个key对应的value<br>
* 如果没有这个key,返回null
* @param key
* @return
*/
public T remove(int key){
//在底层找到对应这个key的节点
Node<T> p=get(key);
if(p==null){
//如果没有这个key,返回null
return null;
}
T oldValue=p.value;
Node<T> next;
while (p!=null) {
next=p.next;
//在这一行中,将p删除
//设置p的next和pre的指针
next.pre=p.pre;
p.pre.next=next;
//p上移,继续删除上一行的p
p=p.up;
}
//更新size,返回旧值
size--;
return oldValue;
}打印整个跳表
public void printSkipList(){
System.out.println("跳表打印开始,总层数为"+level+",节点个数为"+size);
Node<T> first=head;
Node<T> p=first;
int currentLevel=level;
while(first!=null){
//循环first这一层
System.out.print("打印第"+currentLevel+"层: ");
p=first;
while (p!=null) {
System.out.print(p+" ");
p=p.next;
}
first=first.down;
currentLevel--;
System.out.println();
}
System.out.println();
}测试
package datastructure.link.skiplist;
public class Main {
public static void main(String[] args) {
SkipList<Double> list=new SkipList<>();
list.printSkipList();
list.put(1, 2.0);
list.printSkipList();
list.put(3, 4.0);
list.printSkipList();
list.put(2, 3.0);
list.printSkipList();
System.out.println(list.get(2));
System.out.println(list.get(4));
list.remove(2);
list.printSkipList();
}
}
跳表整个java代码
package datastructure.link.skiplist;
import java.util.Random;
public class SkipList<T> {
/**
* 跳表的头尾
*/
public Node<T> head,tail;
/**
* 跳表所含的关键字的个数
*/
public int size;
/**跳表的层数
*
*/
public int level;
/**随机数发生器
*
*/
public Random random;
/**
* 向上一层的概率
*/
public static final double PROBABILITY=0.5;
/**
* 跳表的构造函数
*/
public SkipList(){
//初始化头尾节点及两者的关系
head=new Node<>(Node.HEAD_KEY, null);
tail=new Node<>(Node.TAIL_KEY, null);
head.next=tail;
tail.pre=head;
//初始化大小,层,随机
size=0;
level=0;
random=new Random();
}
public void printSkipList(){
System.out.println("跳表打印开始,总层数为"+level+",节点个数为"+size);
Node<T> first=head;
Node<T> p=first;
int currentLevel=level;
while(first!=null){
//循环first这一层
System.out.print("打印第"+currentLevel+"层: ");
p=first;
while (p!=null) {
System.out.print(p+" ");
p=p.next;
}
first=first.down;
currentLevel--;
System.out.println();
}
System.out.println();
}
/**1. 如果put的key,在跳表中不存在,则在跳表中加入,并由random产生的随机数决定生成几层,返回一个null
* 2. 如果put的key存在,则在跳表中对应的node修改它的value,并返回过去的value
* @param key
* @param value
* @return
*/
public T put(int key,T value){
//首先得到跳表最底层中,最接近这个key的node
Node<T> p=findNearestNode(key);
if(p.key==key){
//如果跳表中有这个key,则返回最底层中,对应这个key的node
//在跳表中,只有最底层的node才有真正的value,只需修改最底层的value就行了
T old=p.value;
p.value=value;
return old;
}
//如果跳表中,没有这个key,那么p就是最底层中,小于这个key,并且最接近这个key的node
//q为新建的最底层的node
Node<T> q=new Node<>(key, value);
//在最底层,p的后面插入q
insertNodeHorizontally(p, q);
//当前level(要与总层数Level进行比较)
int currentLevel=0;
//PROBABILITY为进入下一层的可能性,nextDouble()返回[0,1)
//小于PROBABILITY,说明可能性到达(比如说假设为0.7,小于它的概率就是0.7),进入循环,加入上层节点
while (random.nextDouble()<PROBABILITY) {
//最底层为0,到这里currentlevel为当前指针所在的层,被插入的镜像变量在currentlevel+1层
//所以currentLevel=level时,要在level+1层插入,就要加入一层
if(currentLevel>=level){
addEmptyLevel();
}
//找到q的左边(也就是<=p)第一个能够up的节点,并上浮,赋予p
while (p.up==null) {
p=p.pre;
}
p=p.up;
//创建q的镜像变量z,只有key,没有value,插入在现在的p的后面
Node<T> z=new Node<>(key, null);
insertNodeHorizontally(p, z);
//设置z与q的上下关系
z.down=q;
q.up=z;
//指针上浮
q=z;
currentLevel++;
}
//插入完毕后,size扩大,返回null
size++;
return null;
}
/**返回跳表最底层中,最接近这个key的node<br>
* 如果跳表中有这个key,则返回最底层中,对应这个key的node<br>
* 如果没有这个key,则返回最底层中,小于这个key,并且最接近这个key的node
* @param key
* @return
*/
private Node<T> findNearestNode(int key){
Node<T> p=head;
Node<T> next;
Node<T> down;
while (true) {
next=p.next;
//p先前进到这一层中(一开始在最顶层),p的next>key的位置,然后再考虑向下
if(next!=null&&next.key<=key){
p=next;
continue;
}
down=p.down;
//走到这一步,p在这一层已经无法前进了,就下降一层,在那层进入循环,再往前走
if(down!=null){
p=down;
continue;
}
//到这里,说明已经无法再向下(已经到最底层),无法再向前(当前的p<=key,next>key),最接近key,跳出循环
break;
}
return p;
}
/** 在同一层,水平地,在pre的后面,插入节点now
* @param pre 插入节点前面的节点,应该pre.key小于now.key小于pre.next.key
* @param now 插入的节点
*/
private void insertNodeHorizontally(Node<T> pre,Node<T> now){
//先考虑now
now.next=pre.next;
now.pre=pre;
//再考虑pre的next节点
pre.next.pre=now;
//最后考虑pre
pre.next=now;
}
/**
* 在现在的最顶层之上新加一层,并更新head和tail为新加的一层的head和tail,然后更新总level数(字段level)
*/
private void addEmptyLevel(){
Node<T> p1=new Node<T>(Node.HEAD_KEY, null);
Node<T> p2=new Node<T>(Node.TAIL_KEY, null);
//设置p1的下右
p1.next = p2;
p1.down = head;
//设置p2的下左
p2.pre = p1;
p2.down = tail;
//设置之前头尾的上
head.up = p1;
tail.up = p2;
//设置现在的头尾
head=p1;
tail=p2;
//更新level
level++;
}
/**根据key,返回最底层对应的node,如果不存在这个key,则返回null
* @param key
* @return
*/
public Node<T> get(int key){
//返回跳表最底层中,最接近这个key的node
Node<T> p=findNearestNode(key);
//如果key相同,返回这个node
if(p.key==key){
return p;
}
//如果不相同,返回null
return null;
}
/**在跳表中删除这个key对应的所有节点(包括底层节点和镜像节点)<br>
* 如果确实有这个key,返回这个key对应的value<br>
* 如果没有这个key,返回null
* @param key
* @return
*/
public T remove(int key){
//在底层找到对应这个key的节点
Node<T> p=get(key);
if(p==null){
//如果没有这个key,返回null
return null;
}
T oldValue=p.value;
Node<T> next;
while (p!=null) {
next=p.next;
//在这一行中,将p删除
//设置p的next和pre的指针
next.pre=p.pre;
p.pre.next=next;
//p上移,继续删除上一行的p
p=p.up;
}
//更新size,返回旧值
size--;
return oldValue;
}
}
跳表复杂度
时间
跳表搜索的时间复杂度是 O(logn),插入/删除也是。
空间
对于每层的期待:第一层n,第二层n/2,第三层n/22,...,直到 n/2log n=1。所以,总空间需求:
S = n + n/2 + n/22 + ... + n/2log n < n(1 + 1/2 + 1/22 + ... + 1/2∞) =2n
因此他的空间复杂度为 2n = O(n)
高度
对每层来说,它会向上增长的概率为1/2,则第m层向上增长的概率为1/2m;n个元素,则在m层元素数目的期待为Em = n/2m;当Em = 1,m = log2n即为层数的期待。故其高度期待为 Eh = O(log n)。