基于数组的循环队列C++实现

1. 思想

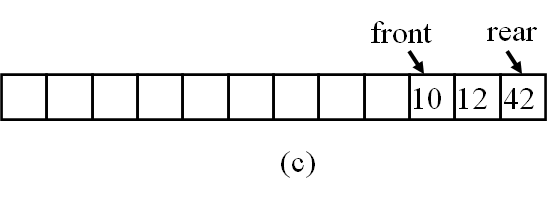
如果不采用循环的方法，那么这种情况下左边一大半空间都无法利用效率低下。为此，考虑循环的思想，即考虑循环的方法，将其视作一个“环”。

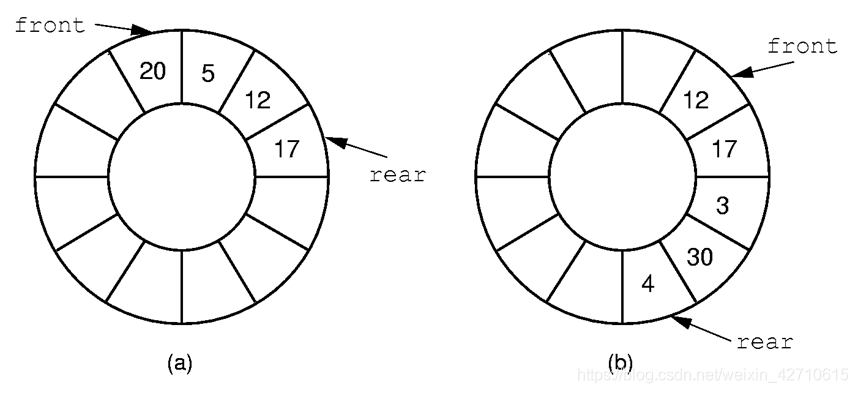
假设建立的数组的大小为$size$，那么环的周期就是$size$，索引为$i$的元素其前一元素为$(i+1)\%size$，后一元素为$(i-1)\%size$。这样就可以将环视作一个正常的数组队列，只是前后元素的表示发生了改变而已。

重点：如何判定队列已满或者队列为空？

如果不预留一个空位的话，是无法判定队列为空或者队列已满的，例如下面这种情况就无法判定到底是空的还是满的。

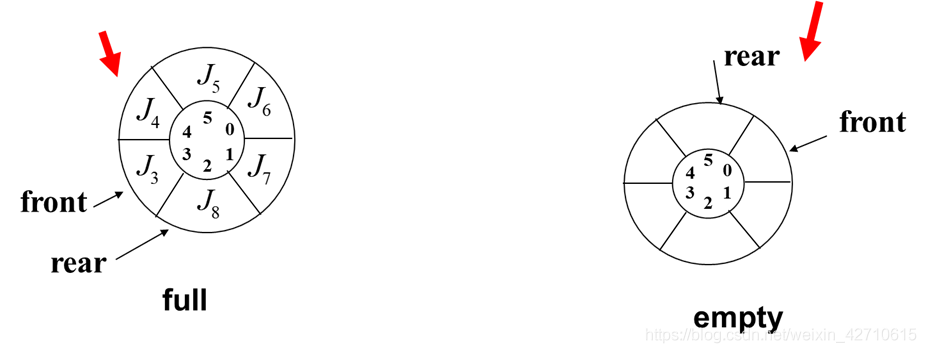
为了能够分别这两种情况就必须在rear和front之间保留一个空位，一旦rear在front的后一位那么说明为空，一旦rear在front的后两位那么说明已满。此时队列最多容纳的元素个数为$size-1$，队列中元素个数可以表示为$(rear+1-front+size)$.

2. C++实现

#include "Queue.h"

/*基于数组的循环队列实现 */
template <class E>
class AQueue : public Queue<E>
{
private:
    int size;     // 最大队列长度
    int front;    // 队首
    int rear;     // 队尾
    E *listArray; // 保存队列元素
public:
    AQueue(int defaultSize = 1000)
    {
        size = defaultSize;
        front = 0;
        rear = -1;
        listArray = new E[size];
    }
    ~AQueue() { delete[] listArray; listArray = NULL;}
    void clear();
    bool enqueue(const E &);    // 入队列
    bool dequeue(E &);          // 出队列
    bool frontValue(E &) const; // 队首元素
    int length() const;         // 队列元素个数
};

template <class E>
void AQueue<E>::clear()
{
    delete[] listArray;
    listArray = new E[size];
    front = 0;
    rear = -1;
}

template <class E>
int AQueue<E>::length() const
{
    return (rear + size - front + 1) % size ;
}

template <class E>
bool AQueue<E>::enqueue(const E &it)
{
    if (length() == size-1)
        return false;
    rear = (rear + 1) % size;
    listArray[rear] = it; 
    return true;
}

template <class E>
bool AQueue<E>::dequeue(E &it)
{
    if (length() == 0)
        return false;
    it = listArray[front]; 
    front = (front+1) % size; 
    return true; 
}

template<class E> 
bool AQueue<E>::frontValue(E &it) const 
{
    if (length() == 0)
        return false; 
    it = listArray[front]; 
    return true; 
}