知识点

KMP算法通常用于解决模式串匹配问题

一个讲解很好的视频： KMP字符串匹配

一 . 字符串的前缀、真前缀、后缀、真后缀

前缀：字符串从左开始的任意子串（或者说是字符串的任意首部）

真前缀（又称前缀真子串）：是指不包含本身的前缀。

后缀定义：字符串从右开始的任意子串（或者说是字符串的任意尾部）

真后缀（又称后缀真子串）：是指不包含本身的后缀。

以x=“ABCD”为例：

前缀：空串，“A”，“AB”，“ABC”，“ABCD”；

后缀：空串，“D”，“DC”、“DCB”，“DCBA”；

类比中学阶段集合概念，真子集就是真前缀，空集就是空字符，子集就是所有的前缀，后缀同理。

二 . KMP算法原理

（1）暴力：

将子串（较短的字符串）的第一位与长串进行一位一位的比较，若出现一位不匹配，整个子串向后移动一位。

初始状态：（i，j作为指针，标记搜索的位置）

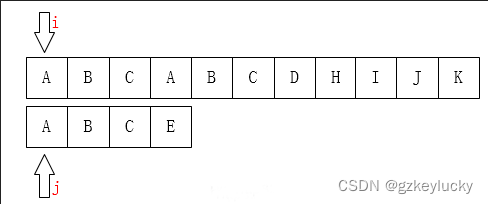
找到未匹配的状态：

子串向后移动一位：

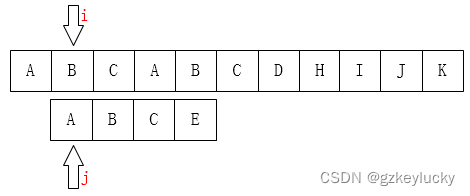
暴力搜索会出现子串与长串完全不匹配的情况，会浪费大量的时间。

2.KMP算法的搜索移动

字符组1：

初始状态：

第一次不匹配移动后的状态：

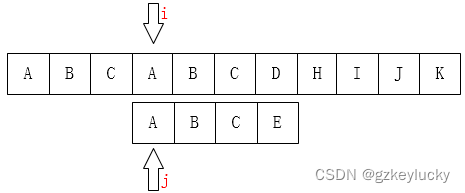
字符组2：

初始状态：

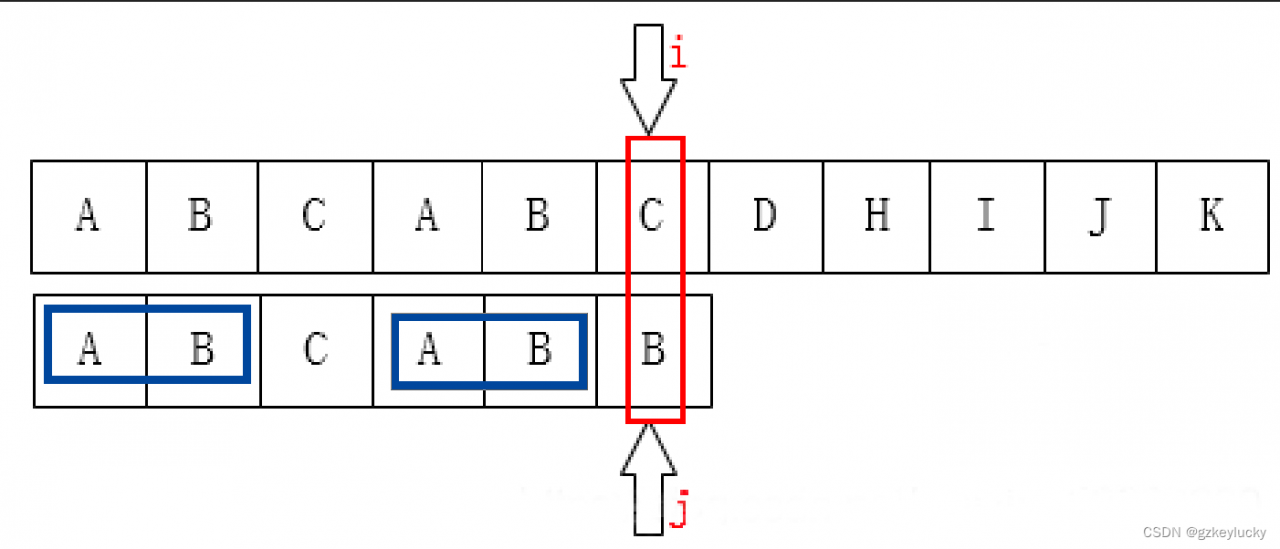
第一次不匹配的移动后的状态：

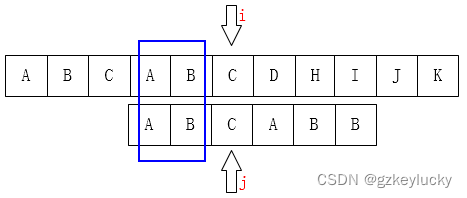
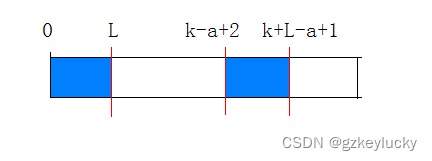
3.求前缀和后缀的长度

以子串ABABC为例：

子串长度	子串	前后缀长度（小于子串长度）
1	A	0
2	AB	0
3	A B A	1
4	AB AB	2
5	ABABC	0

表格中前后缀长度就是next数组。

注意：最长相同前后缀不能是字符串本身

模板题

例题：洛谷 P3375 【模板】KMP字符串匹配

题目描述

给出两个字符串 $s_1$ 和 $s_2$ ，若 $s_1$ 的区间 [l, r] 子串与 $s_2$ 完全相同，则称 $s_2$ 在 $s_1$ 中出现了，其出现位置为 l。
现在请你求出 $s_2$ 在 $s_1$ 中所有出现的位置。

定义一个字符串 s 的 border 为 s 的一个非 s 本身的子串 t，满足 t 既是 s 的前缀，又是 s 的后缀。
对于 $s_2$ ，你还需要求出对于其每个前缀 s' 的最长 border t' 的长度。

输入格式

第一行为一个字符串，即为 $s_1$ 。
第二行为一个字符串，即为 $s_2$ 。

输出格式

首先输出若干行，每行一个整数，按从小到大的顺序输出 $s_2$ 在 $s_1$ 中出现的位置。
最后一行输出 $|s_2|$ 个整数，第 i 个整数表示 $s_2$ 的长度为 i 的前缀的最长 border 长度。

输入输出样例

输入 #1

ABABABC
ABA

输出 #1

1
3
0 0 1

说明/提示

样例 1 解释

对于 $s_2$ 长度为 3 的前缀 ABA，字符串 A 既是其后缀也是其前缀，且是最长的，因此最长 border 长度为 1。

数据规模与约定

本题采用多测试点捆绑测试，共有 3 个子任务。

Subtask 1（30 points）： $|s_1| \leqslant 15 , |s_2| \leqslant 5$ 。
Subtask 2（40 points）： $|s_1| \leqslant 10^4$ ， $|s_2| \leqslant 10^2$ 。
Subtask 3（30 points）：无特殊约定。

对于全部的测试点，保证 $1 \leqslant |s_1|,|s_2| \leqslant 10^6$ ， $s_1$ , $s_2$ 中均只含大写英文字母。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <string>
using namespace std;
const int maxn=1e5+5;
string a,b;
int len1,len2,Next[maxn],next2[maxn]; 
void table(string b) //求前缀表
{
	next2[0]=0;  //定义一个数组：用于存储截止至目前i字符串前缀的长度
	int i=1;  //从字符串第二个字符开始计算
	int len=0; //用于统计前缀的长度
	while(i<b.length())
	{
		if(b[i]==b[len]) //如果第i项的字母与len位的字母相同
		{
		len++; //前缀的长度加1；
		next2[i]=len; //当指针搜到i位置的时候，前缀的长度
		i++; //指针后移，进行下一次查找
		}
		else//如果第i项的字母与len位的字母不相同
		{
		    if(len>0) //如果此时的前缀长度不为0（小心下标越界）
		    {
		        len=next2[len-1]; 
	            //前缀长度等于数组存的第len-1的位置的长度（遗留问题）
		    }
		    else
		    {
		        next2[i]=len; //数组中存入0
		        ++i;//将指针i向后移动1位
		    }
		}
	}
}

void kmp(string a,string b) //KMP算法的核心
{
	int i=0,j=0; //定义两个指针
	Next[0]={-1}; //把用于存前缀表的数组第一位改成-1
	len1=a.length();  //记录长串的长度
	len2=b.length(); //记录短串的长度
	for(int i=1;i<=len2-1;++i)
	{
		Next[i]=next2[i-1]; //将前缀表的位置向后移动1位
	}
	
	while(i<=len1-1) //搜到长串的最后一个字母前
	{
		if((j==len2-1)&&(a[i]==b[j])) //如果子串全部与长串匹配
		{
			cout<<i-j+1<<endl; //输出子串s2在长串s1的位置
			j=Next[j];     
                //*是难点也是关键点！
	    //如果a[i]和b[j]中字符不同，则视为匹配失败，将j的值退回至Next[j]的位置上，直至两者相同
	    //好处：减少逐步向后移进行不必要的比较
		}
		if ((a[i]==b[j])||(j==-1)) 
            //如果未到子串的最后一位相等，或子串第一位序号j对应的是前缀表的-1
		{
			i++;
			j++;
			//两个指针都向后移
		}
		else j=Next[j];	
	}
}

int main()
{
	cin>>a>>b;
	table(b); //前缀表只需处理子串
	kmp(a,b);
	for(int i=0;i<=len2-1;++i)
	{
	cout<<next2[i]<<" ";  //输出前缀表
	}
	return 0;
}

KMP算法的优化：（待填坑）

有些时候，KMP算法还不够快，比如以下的情况：

原文链接：https://blog.csdn.net/gzkeylucky/article/details/126801252