数据结构 - 统计二叉树度为0/1/2的结点个数（递归）

0. 变量/函数声明

树的结构体

#define ElemType int

typedef struct BiTNode {
    ElemType data; // 数据域
    struct BiTNode *l_child, *r_child; // 左右孩子指针
} BiTNode, BstNode, *BiTree;

函数声明

int GetNodeCountOfZeroDegree(BiTree &T); // 统计二叉树中度为0的结点数（递归）
int GetNodeCountOfOneDegree(BiTree &T); // 统计二叉树中度为1的结点数（递归）
int GetNodeCountOfTwoDegree(BiTree &T); // 统计二叉树中度为2的结点数（递归）

1. 统计结点数

思路：

f(T) = 0; // T==NULL
f(T) = f(T->l) + f(T->r) + 1; // 满足条件的结点（度为0/1/2）
f(T) = f(T->l) + f(T->r); // 不满足条件的结点

统计度为0的结点数

/**
 * 统计二叉树中度为0的结点数（递归）
 * @param T
 * @return 度为0的结点数
 */
int GetNodeCountOfZeroDegree(BiTree &T) {
    if (T == NULL) {
        return 0;
    } else if (T->l_child == NULL && T->r_child == NULL) {
        // 度为0的结点，累加
        return GetNodeCountOfZeroDegree(T->l_child) + GetNodeCountOfZeroDegree(T->r_child) + 1;
    } else {
        // 度为1或2的结点，不累加
        return GetNodeCountOfZeroDegree(T->l_child) + GetNodeCountOfZeroDegree(T->r_child);
    }
}

统计度为1的结点数

/**
 * 统计二叉树中度为1的结点数（递归）
 * @param T
 * @return 度为1的结点数
 */
int GetNodeCountOfOneDegree(BiTree &T) {
    if (T == NULL) {
        return 0;
    } else if ((T->l_child == NULL && T->r_child != NULL) || (T->l_child != NULL && T->r_child == NULL)) {
        // 度为1的结点，累加
        return GetNodeCountOfOneDegree(T->l_child) + GetNodeCountOfOneDegree(T->r_child) + 1;
    } else {
        // 度为0或2的结点，不累加
        return GetNodeCountOfOneDegree(T->l_child) + GetNodeCountOfOneDegree(T->r_child);
    }
}

统计度为2的结点数

/**
 * 统计二叉树中度为2的结点数（递归）
 * @param T
 * @return 度为2的结点数
 */
int GetNodeCountOfTwoDegree(BiTree &T) {
    if (T == NULL) {
        return 0;
    } else if (T->l_child != NULL && T->r_child != NULL) {
        // 度为2的结点，累加
        return GetNodeCountOfTwoDegree(T->l_child) + GetNodeCountOfTwoDegree(T->r_child) + 1;
    } else {
        // 度为1或0的结点，不累加
        return GetNodeCountOfTwoDegree(T->l_child) + GetNodeCountOfTwoDegree(T->r_child);
    }
}

2. 运行情况

INPUT

{3, 1, 8, 7, 5, 6, 9}

插入时按照排序树插入，当然这不是本文的重点，没有给代码

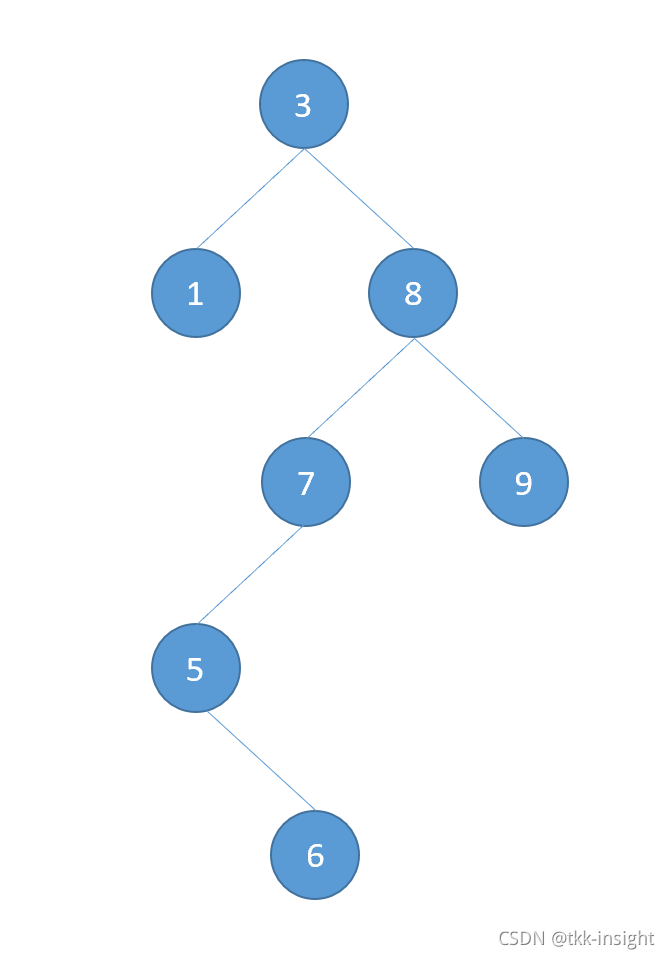
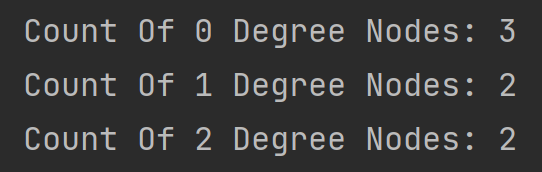
OUTPUT