树状数组 是一种被用于解决区间问题的算法。位思想和树思想是核心。
先看一个例子。
例
请你设计一个数据结构,维护一个整形数列 a aa,支出以下几种操作:
- 将 a i a_iai 的值加上为 x xx;
- 求 ∑ k = l r a k \sum_{k=l}^ra_kk=l∑rak
保证操作次数、数组长度均小于 5 × 1 0 5 5×10^55×105.
显然朴素算法会超时。不妨想,优化时间复杂度的方法是用一个元素表示多个元素的信息。如果用二分思想,单次修改或查询的时间复杂度将会下降到 log n \log nlogn 的水平。(线段树)
这里我们使用另一种方式维护这个数组。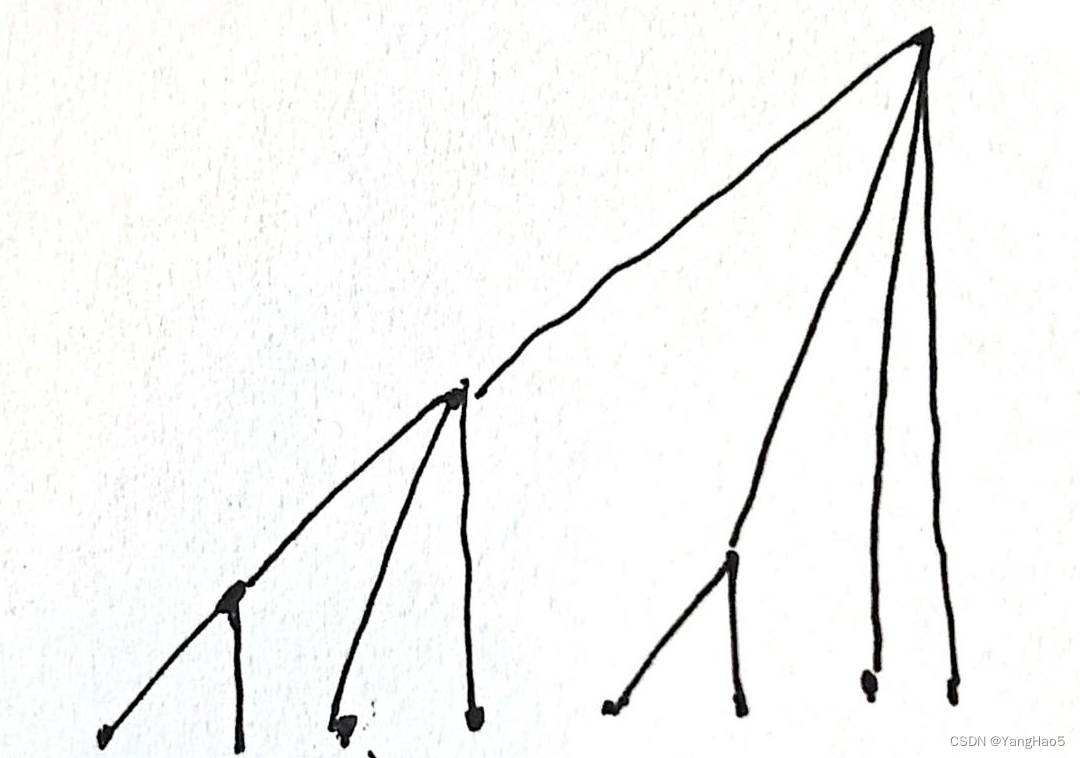
在这种维护模式下即可实现 O ( log n ) O(\log n)O(logn) 复杂度的修改和查询。
下面我们探究每次修改或查询时,从叶子节点到根节点的路径的节点的编号的规律。
这种建树方式与 2 的若干次幂有关,不难想到观察编号的二进制表示。再写出每个节点管理的点数量(记作 lowbit)。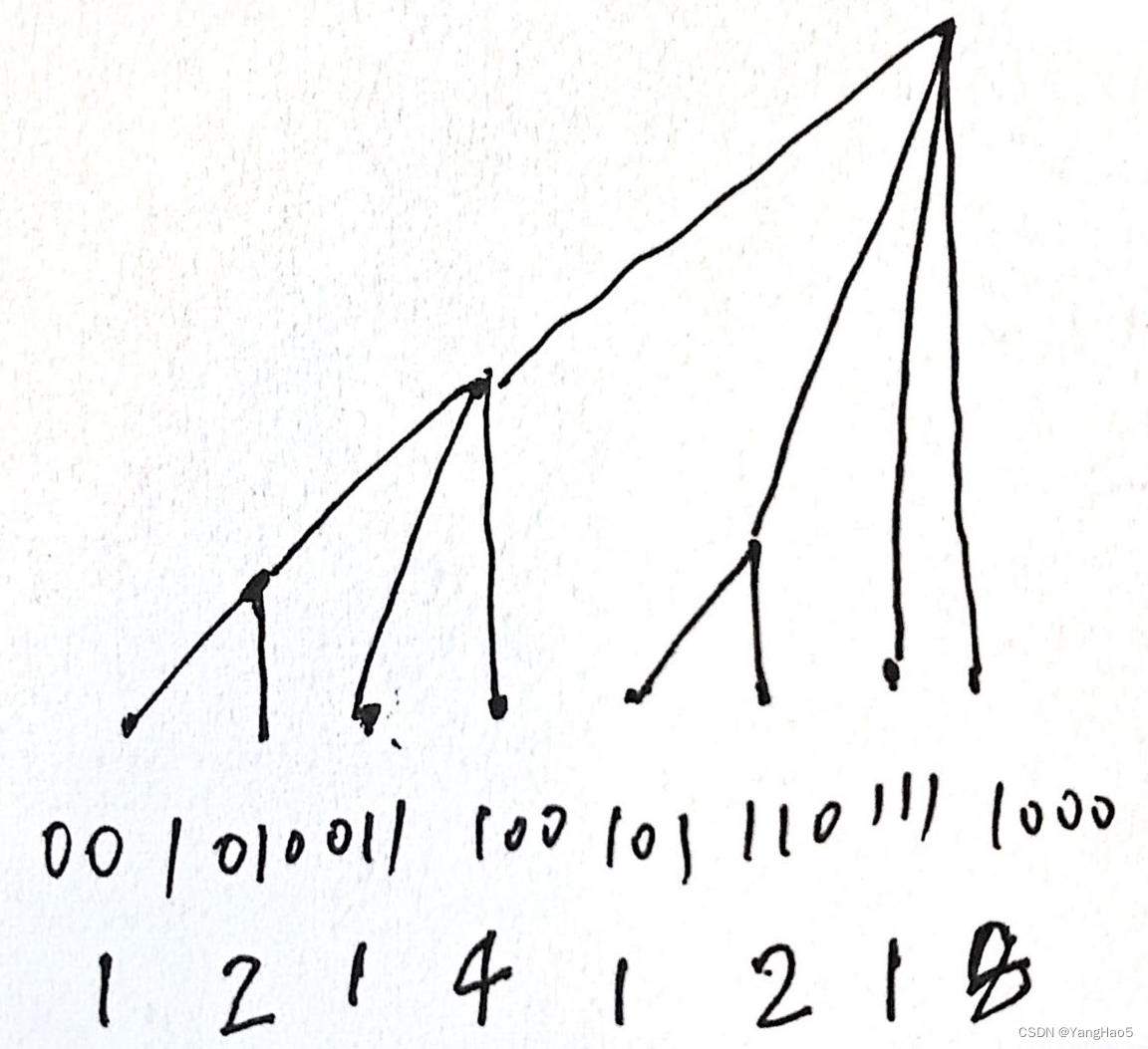
经过推导我们不难发现,一个节点管理的点数量=只保留二进制下最右边的1构成的二进制数。比如6=110(2),最右边的1在二号位,所以6号节点管理10(2)=2个结点。
现在我们考虑如何计算上述公式。
考虑使用 & 运算。他能帮我们消去多余的1。如果我们能构造一个跟原来的数 a 完全相反的数 b(二进制意义下),但是最右边的1仍保留。那么我们就能得到 a & b。
考虑如何得到一个与 a 完全相反的数。回顾所学知识,由计算机存储负数为补码可以发现,b = -a 能完美解决问题。(因为补码=反码+1)
由构图方式可知,一个节点与父亲的距离=这个节点管辖的节点数。这样,我们就实现了树状数组的构建与维护。下面给出例题的代码。
#include <cstdio>
#include <cstdlib>
#include <cstring>
//因为要构建一个完整的树状数组,所以需要双倍空间
const int MAXN=1000010;
int n, m;
int tree[MAXN];
inline int lowbit (int x){
return x&(-x);
}
inline int read (){
int x=0, flag=1; char c;
do {
c=getchar ();
if ('-'==c) flag=0;
}while ('0'>c||'9'<c);
while ('0'<=c&&'9'>=c)
x=x*10+c-48, c=getchar ();
return flag?x:(-x);
}
void change (int x, int d){
int now=x;
while (now<=n){
tree[now]+=d;
now+=lowbit (now);
}
}
int query (int x){
int now=x, sum=0;
while (now){
sum+=tree[now];
now-=lowbit (now);
}
return sum;
}
int s1, s2, s3;
int main(){
memset (tree, 0, sizeof (tree));
n=read (); m=read ();
for (int i=1; i<=n; ++i)
change (i, read ());
for (int i=1; i<=m; ++i){
s1=read (); s2=read (); s3=read ();
if (1==s1)
change (s2, s3);
else
printf ("%d\n", query (s3)-query (s2-1));
}
}
版权声明:本文为YangHao5原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。