数据结构与算法整理4——栈及其操作(C语言)
目录
1、栈的基本概念与特点
栈和队列也是线性表,只是操作受限制的线性表,他们线性表的区别在于线性表可以在在任意位置插入或删除元素,而栈只能在栈顶操作,队列只能在队尾操作。
1.1栈的特点:后进先出(LIFO)可看做装电池,只能对栈顶进行操作。
1.2存储方式:顺序存储和链式存储。
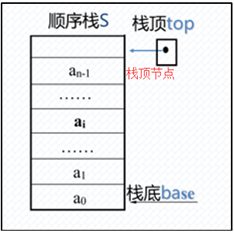
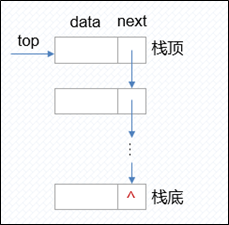
有n个元素的栈的顺序存储 栈的链式存储
2、栈的两种存储结构的基本操作,如何入栈,出栈,判空
操作 | 栈 | |
存储方式类型 | 顺序栈 | 链式栈 |
定义数据类型 | Typedef struct{ Int stack[maxsize]; Int top; }sequencestack; | Typedef struct snode{ Int data; Int snode *next; }singlelinkednode; |
初始化 | S->top=0; |
|
取栈顶 | *d=S.stack[S.top-1];
| Singlelinkednode *p=head->next; *d=p->data; |
入栈 | S->stack[S->top]=x; S->top++; 移动top指针 | Singlelinkednode *p; p->data=x; p->next=head->next;//先执行 head->next=p; //后执行
|
出栈 | S->top--; 直接移动top指针,不用删除原栈顶 | head->next=head->next->next; free(p);//需要释放出栈的元素
|
判空 | if(S->top==0) printf(“stack is empty”); | If(head->next==null) Printf(“stack is empty”); |
3、栈的应用举例(进制转换,递归,迷宫,表达式求值等)
栈的应用 | 内容 |
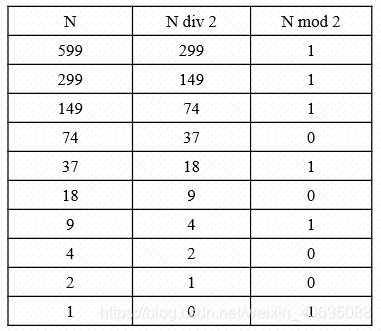
进制转换 | 算法原理:辗转相除法算法公式:N=(N div 2) * 2 +N mod 2
|
递归 |
|
迷宫 |
|
表达式求值 | 例1:A+(B-C/D)*E(也称为中缀表达式) 前缀表达式为:+A*-B/CDE 即运算符在数值前面 后缀表达式为:ABCD/-E*+ 运算符在数值后面 例2:[(a+b)+c*(d+e)+f]*(g+h) 前缀表达式为:*++ab*+cdeg+gh 后缀表达式为:ab+cde+*+f+gh+* |
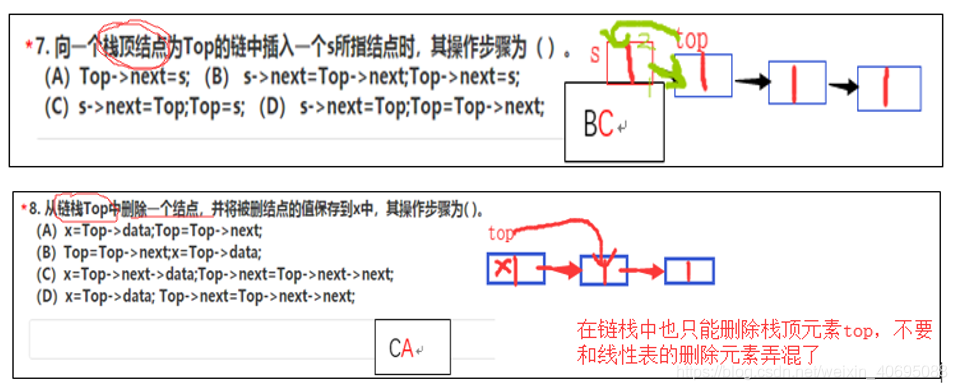
4、栈相关的几个例题

5、栈的操作代码实现(C语言)
(1)入栈问题:
#include "stdio.h"
#include "stdlib.h"
typedef struct stack{
int data;
struct stack *next;
}Lstack,*LinkStrack; //Lstrack表示链式栈中结点的类型, LinkStrack是申明了一个指向节点的指针数据类型
int pushstrack(LinkStrack head,int n){ //将元素n压入栈 此时head指的是直接指向栈顶的头结点
LinkStrack p=(Lstack *)malloc(sizeof(Lstack)); //创建一个新的节点
if(p==NULL){
printf("内存不足,无法入站");
return 0;
}
p->data=n;
p->next=head->next; //让p结点成为栈顶
head->next=p; //把head结点的指针指向新的栈顶p 保持head始终指向最新的栈顶
return 1;
}
int gettop(LinkStrack top){
return top->data;
}
int main(){
LinkStrack S;
int e;
//InitialStack(S);
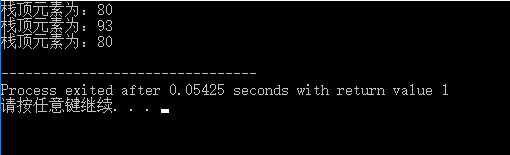
pushstrack(S,13);
pushstrack(S,93);
pushstrack(S,80);
printf("栈顶元素为:%d\n",gettop(S));
return 1;
} (2)顺序存储方式的栈的操作
#include "stdio.h"
#include "stdlib.h"
//顺序存储的栈的应用
#define maxsize 30
//定义栈的结构体
struct stack
{
int top;
int stack[maxsize];
}; //pseqstack S 相当于 stack *S
typedef struct stack *pseqstack;
//创建一个栈
pseqstack CreatStack(void){
pseqstack s=(pseqstack)malloc(sizeof(struct stack));
if(s==NULL)
printf("溢出!!");
else
s->top=0;
return s;
}
//进栈(先进后出)
void pushstack(pseqstack s,int n){
if(s->top>=maxsize)
{
printf("栈已满,无法插入!");
}
else
{
s->top++; //top上移 s->top指的是栈顶的位置 注意两者顺序
s->stack[s->top]=n; //把栈顶的位置的值放入n
}
}
//删除栈顶(出栈)
int popstack(pseqstack s,int e){
if(s->top<0)
{
printf("栈已空,无法删除!");
return 0;
}
else
{
e=s->stack[s->top]; //注意两者顺序
s->top--; //直接把top向下移一个单位,被删除的栈点(原栈顶)存储位置没有变没有被释放
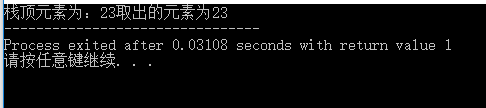
printf("取出的元素为%d",e);
return 1;
}
}
//取出栈顶的元素
int gettopele(pseqstack s){
return s->stack[s->top];
}
//main测试函数
main(){
pseqstack S;
int e;
//Initialstack(S);
S=CreatStack();
pushstack(S,11);
pushstack(S,23);
printf("栈顶元素为:%d",gettopele(S));
popstack(S, e);
} 
(3)链式存储方式的栈的操作
#include "stdio.h"
#include "stdlib.h"
typedef struct stack{
int data;
struct stack *next;
}Lstack,*LinkStrack; //Lstrack表示链式栈中结点的类型, LinkStrack是申明了一个指向节点的指针数据类型
void InitialStack(Lstack * * head){ //初始化带头结点的链式栈 但是 Lstack * * head是什么意是呢?
if((*head=(Lstack *)malloc(sizeof(Lstack)))==NULL){
exit(1);
}
(*head)->next=NULL;
}
//入栈
LinkStrack pushstrack(LinkStrack top,int n){ //将元素n压入栈 此时top指的是直接指向栈顶的指针
LinkStrack temp=(Lstack *)malloc(sizeof(Lstack)); //创建一个新的节点
if(temp==NULL){
printf("内存不足,无法入站");
return 0;
}
temp->data=n;
temp->next=top; //把栈顶指针指向新入栈的元素
top=temp;
return top; //返回栈顶指针
}
//入栈方法二
//int pushstrack(LinkStrack head,int n){ //将元素n压入栈 此时head指的是直接指向栈顶的头结点
// LinkStrack p=(Lstack *)malloc(sizeof(Lstack)); //创建一个新的节点
// if(p==NULL){
// printf("内存不足,无法入站");
// return 0;
// }
// p->data=n;
// p->next=head->next; //让p结点成为栈顶
// head->next=p; //把head结点的指针指向新的栈顶p 保持head始终指向最新的栈顶
// return 1;
//}
//出栈 方法一 可以成功
//LinkStrack popstack(LinkStrack top,int e){
// LinkStrack temp;
// if(top==NULL)
// {
// printf("error\n");
// return NULL;
// }
// e=top->data; //将栈顶元素返回给e
// temp=top; //将栈顶指针暂时存放在temp指针里面,使temp指针也指向栈顶
// top=temp->next; //temp->next的值是原栈顶的下面一个元素的data域的地址,所以 top=temp->next就是把top指向原栈顶的下一个元素的data域,由此打到出栈的目的
// free(temp); //释放中间指针temp 但是没有释放掉原栈顶
// printf("栈顶元素为:%d\n",top->data);
// return top;
//}
//出栈方法二
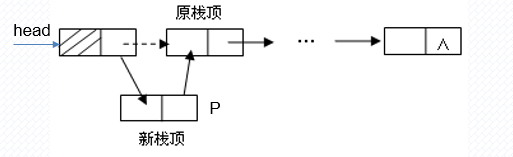
int popstack(Lstack *head,int e){ //head是头指针,指向栈顶
LinkStrack p=head->next; //p就是head->next是原栈顶
if(p==NULL)
{
printf("error\n");
return NULL;
}
e=p->data; //将栈顶元素返回给e
printf("栈顶元素为:%d\n",e);
head->next=p->next; //将头指针指向原栈顶的下一个元素的data域
free(p); //释放原栈顶的内存p
return 1;
}
//取栈顶元素
int gettop(LinkStrack top){
return top->data;
}
int main(){
LinkStrack S;
int e;
//InitialStack(S);
S=pushstrack(S,13);
S=pushstrack(S,93);
S=pushstrack(S,80);
printf("栈顶元素为:%d\n",gettop(S));
popstack(S,e);
printf("栈顶元素为:%d\n",gettop(S));
return 1;
}