加权最小二乘法
参考文献
逻辑
- 普通最小二乘法OLS
- 加权最小二乘法
(1) 广义最小二乘法(加权最小二乘法是广义最小二乘法的一种特殊情形)
(2) 加权最小二乘法
(3) 广义最小二乘 & 普通最小二乘模型 的转换
一 普通最小二乘法OLS
普通最小二乘法的回归模型:Y = X β + ϵ Y=Xβ+\epsilonY=Xβ+ϵ
Y : n ∗ 1 , X : n ∗ p , ϵ : p ∗ 1 , Y: n∗1, X: n∗p, \epsilon: p∗1,Y:n∗1,X:n∗p,ϵ:p∗1, 由于有常数项,所以自变量个数其实是 p − 1 p-1p−1 个.
普通最小二乘法就是使得 残差平方和 最小:R S S ( β ) = ∣ ∣ Y − X β ∣ ∣ 2 = ( Y − X β ) T ( Y − X β ) . RSS(β)=||Y−Xβ||^2=(Y−Xβ)^T(Y−Xβ).RSS(β)=∣∣Y−Xβ∣∣2=(Y−Xβ)T(Y−Xβ). β \betaβ 的估计:β ^ = ( X T X ) − 1 X T Y . \hat{\beta}=(X^TX)^{−1}X^TY.β^=(XTX)−1XTY.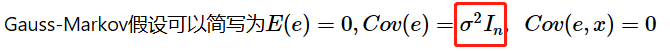
在该假设下,估计 β ^ \hat{\beta}β^ 是 β ββ 所有线性无偏估计中方差最小的。
二 加权最小二乘法
加权最小二乘法是广义最小二乘法的一种特殊情形,普通最小二乘法是一种特殊的加权最小二乘法。
普通最小二乘法 ∈ \in∈ 加权最小二乘法 ∈ \in∈ 广义最小二乘法
1 广义最小二乘法
广义最小二乘法模型:![]()
Σ ΣΣ 是我们已知的一个 n ∗ n n∗nn∗n 正定对称矩阵,其中 σ 2 σ^2σ2 不一定是已知的。且不要求误差项 ϵ \epsilonϵ 的各分量间互不相关了。
广义最小二乘法就是使得 广义残差平方和 最小:R S S ( β ) = ( Y − X β ) T Σ − 1 ( Y − X β ) . RSS(β)=(Y−Xβ)^TΣ^{-1}(Y−Xβ).RSS(β)=(Y−Xβ)TΣ−1(Y−Xβ). β ββ 的估计:β ^ = ( X T Σ − 1 X ) − 1 X T Σ − 1 Y . \hat{β}=(X^TΣ^{-1}X)^{-1}X^TΣ^{-1}Y.β^=(XTΣ−1X)−1XTΣ−1Y.
2 加权最小二乘法
加权最小二乘法:对上述的 Σ ΣΣ 取一种特殊的矩阵——对角阵,且这个对角阵的对角元都是常数,也就是权重 w i w_iwi 的倒数.
C o v ( ϵ ) = σ 2 Σ = σ 2 ( 1 w 1 0 ⋯ 0 0 1 w 2 ⋯ 0 ⋮ ⋮ ⋱ ⋮ 0 0 ⋯ 1 w n ) Cov(\epsilon)=σ^2Σ=σ^2 \left( \begin{matrix} \frac{1}{w_1} & 0 & \cdots & 0 \\ 0 & \frac{1}{w_2} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \frac{1}{w_n} \\ \end{matrix} \right)Cov(ϵ)=σ2Σ=σ2⎝⎜⎜⎜⎛w110⋮00w21⋮0⋯⋯⋱⋯00⋮wn1⎠⎟⎟⎟⎞ ω i ω_iωi 表示第 i ii 个样本在回归里的权重,从上式可以看出来,具有较大权的样本具有较小的方差,因此,它在回归问题里显得更加重要。
不妨用 W WW 来表示权重矩阵,那么 W = Σ − 1 W=Σ^{-1}W=Σ−1,此时,我们用广义最小二乘的方法来求系数的估计,即最小化广义残差平方和:R S S ( β ) = ( Y − X β ) T W ( Y − X β ) . RSS(β)=(Y−Xβ)^TW(Y−Xβ).RSS(β)=(Y−Xβ)TW(Y−Xβ). β ββ 的估计结果为:β = ( X T W X ) − 1 X T W Y . β^=(X^TWX)^{−1}X^TWY.β=(XTWX)−1XTWY.
3 加权最小二乘 & 普通最小二乘模型 的转换
Σ − 1 Σ^{-1}Σ−1 的平方根 C CC:
C = W = Σ − 1 ( w 1 0 ⋯ 0 0 w 2 ⋯ 0 ⋮ ⋮ ⋱ ⋮ 0 0 ⋯ w n ) C=\sqrt{W}=\sqrt{Σ^{-1}} \left( \begin{matrix} \sqrt{w_1} & 0 & \cdots & 0 \\ 0 & \sqrt{w_2} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \sqrt{w_n} \\ \end{matrix} \right)C=W=Σ−1⎝⎜⎜⎜⎛w10⋮00w2⋮0⋯⋯⋱⋯00⋮wn⎠⎟⎟⎟⎞
对加权最小二乘法回归模型 Y = X β + ϵ Y=Xβ+\epsilonY=Xβ+ϵ 的每一项乘以 C CC:C Y = C X β + C ϵ . CY=CXβ+C\epsilon.CY=CXβ+Cϵ. C ϵ C\epsilonCϵ 的协方差阵为:V a r ( C ϵ ) = C V a r ( ϵ ) C T = C σ 2 Σ C T = C σ 2 ( C T C ) − 1 C T = σ 2 I n . Var(C\epsilon)=CVar(\epsilon)C^T=C\ σ^2Σ\ C^T=C\ σ^2(C^TC)^{-1}\ C^T=σ^2I_n.Var(Cϵ)=CVar(ϵ)CT=C σ2Σ CT=C σ2(CTC)−1 CT=σ2In.就是满足 G a u s s − M a r k o v Gauss-MarkovGauss−Markov 假设的普通线性回归模型了.
不妨重新对变量命名:Z = M β + d Z=Mβ+dZ=Mβ+d其中,Z = C Y = ( w 1 y 1 w 2 y 2 ⋮ w n y n ) Z=CY= \left( \begin{matrix} \sqrt{w_1}\ y_1 \\ \sqrt{w_2}\ y_2 \\ \vdots \\ \sqrt{w_n}\ y_n \\ \end{matrix} \right)Z=CY=⎝⎜⎜⎜⎛w1 y1w2 y2⋮wn yn⎠⎟⎟⎟⎞
M = C X = ( w 1 w 1 x 11 ⋯ w 1 x 1 , p − 1 w 2 w 2 x 21 ⋯ w 2 x 2 , p − 1 ⋮ ⋮ ⋱ ⋮ w n w n x n 1 ⋯ w n x n , p − 1 ) M=CX= \left( \begin{matrix} \sqrt{w_1} & \sqrt{w_1}\ x_{11} & \cdots & \sqrt{w_1}\ x_{1,p-1} \\ \sqrt{w_2} & \sqrt{w_2}\ x_{21} & \cdots & \sqrt{w_2}\ x_{2,p-1} \\ \vdots & \vdots & \ddots & \vdots \\ \sqrt{w_n} & \sqrt{w_n}\ x_{n1} & \cdots & \sqrt{w_n}\ x_{n,p-1} \\ \end{matrix} \right)M=CX=⎝⎜⎜⎜⎛w1w2⋮wnw1 x11w2 x21⋮wn xn1⋯⋯⋱⋯w1 x1,p−1w2 x2,p−1⋮wn xn,p−1⎠⎟⎟⎟⎞
d = C ϵ d=C\epsilond=Cϵ 新模型用普通最小二乘所估计出来的 β ^ \hat{β}β^ 和原模型(加权最小二乘模型)是一样的,而且线性无偏方差最小的性质和分布,检验等都可以用起来了,如 R 2 R^2R2 及显著性检验等来看拟合的好坏。