SIFT简化版理解

1. 构建高斯差分金字塔

高斯金字塔

将原始图像不断降阶采样，原图像为金字塔的第一层，每次降采样得到金字塔的一层，整个金字塔共n层。金字塔层数又原始图像的大小和塔顶图像的大小共同决定。
$n=lo{g}_{2}min(M,N)-t,t\in [0,lo{g}_{2}min(M,N)]$
其中M，N分别为原始图像的shape, t为塔顶图像大小取对数。如512x512的图像，有

此处，t = $lo{g}_{2}1$=1
为了让尺度体现连续性，高斯金字塔在简单降采样的基础上，添加了高斯滤波。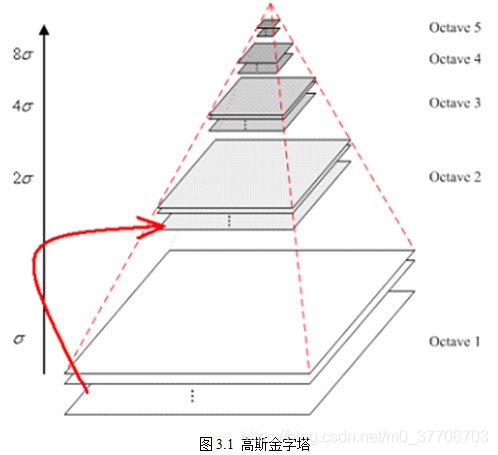

对最初每层一张图像进行不同参数的高斯滤波，使得每层得到一组(Octave)图像大小相同，但模糊程度不同的大小。每一组的多张图像称为层Interval图像。降采样时，高斯金字塔上一层图像的初始图像是由前一组的倒数第三张图像隔点采样得到。如下图所示。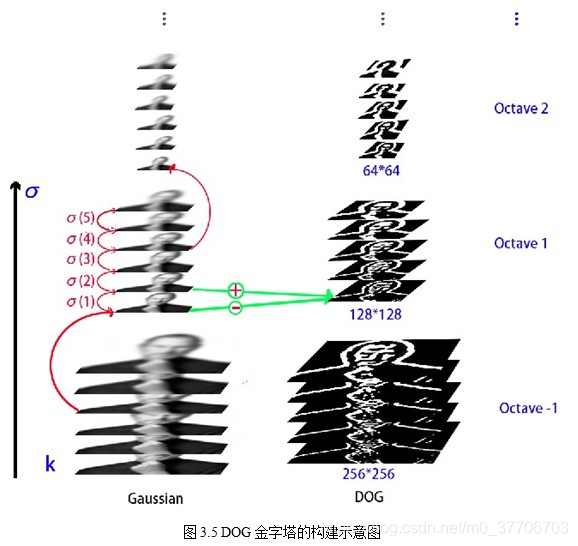

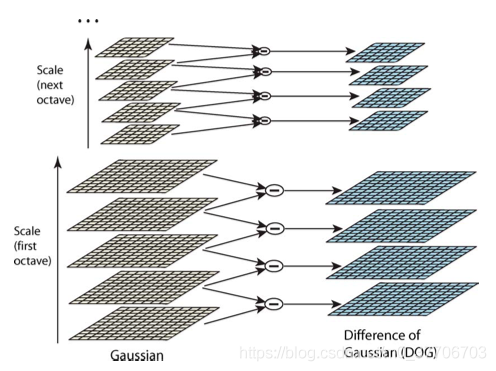
高斯差分金字塔

对高斯金字塔每组中的图像执行上下两层相减，得到差分图像。

2. 空间极值点检测

关键点是DOG空间的局部极值点，而局部极值点是通过将该图像与上下相邻的图像比较得到。如图，中间的检测点要和它的8个相邻点以及相同尺度上下相邻图像对应的9个点进行比较，一共8+9x2=26个点进行比较，得到极大值或极小值点。最后利用子像素插值得到连续空间的极值点。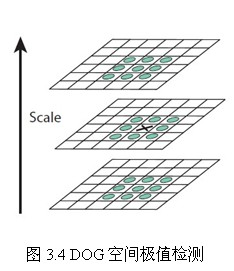

为了在DOG空间每组中检测S个尺度的关键点，由于每组第一张和最后一张图像无法完成上述的比较，所以需要S+2个高斯差分图像。同时，高斯差分图像是由高斯金字塔图像相减得到，故高斯金字塔每组需要S+3个图像。如上图高斯差分金字塔形成过程：高斯金字塔每组5张图像，对应差分图像每组4张。

构建尺度空间需要确定的参数

$\sigma$:尺度空间坐标
$O$:金字塔的总组（octave)数
$S$:每组组内总层数 应该是要检测的关键点的数目，总层数为S+3
关键点的尺度坐标计算如下：
$\sigma (o,s)={\sigma }_0{2}^{o+\frac{s}{S}}o\in [0,...,O-1],s\in [0,...,S+2]$
其中s表示层索引，从0开始，下图从1开始。不能和S搞混。
最开始建立高斯金字塔时，第0组第0个图像并不是原图像，需要对其模糊。若(1)已经进行了${\sigma }_{-1}=0.5$的高斯模糊，那么(2)再将图像的尺寸通过双线性差值扩大一倍，相当于${\sigma }_{-1}=1.0$，得到第0组第0个图像。
定义$k=2^{\frac{1}{S}}$
将下图n换成S,每组共有S+3层，有每层的尺度$\sigma =k^s{\sigma }_0=(2^{\frac{1}{S}}{)}^s{\sigma }_0$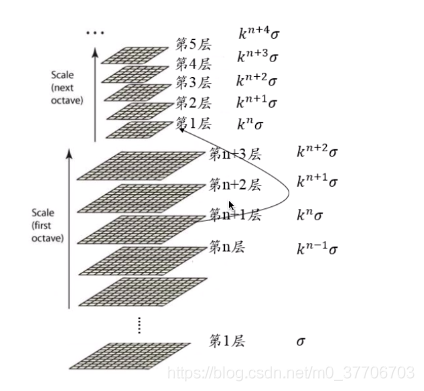

在构建高斯金字塔时，组内每层的尺度坐标按如下公式计算：
$\sigma (s)=\sqrt{(k^s{\sigma }_0{)}^2-(k^{s-1}{\sigma }_0{)}^2}$
这里${\sigma }_0=\sqrt{1.6^2-0.5^2}=1.52$
用于一次生成组内不同尺度的高斯图像，组内下一层图像由前一层图像按$\sigma (s)$进行高斯模糊取得。
在计算组内某一层图像的尺度时，直接用如下公式计算：
$\sigma \_oct(s)={\sigma }_0{2}^{\frac{s}{S}}$，与上式$\sigma =k^{n-1}{\sigma }_0=(2^{\frac{1}{S}}{)}^{n-1}{\sigma }_0$保持一致，因为上图索引从1开始，这里从0开始。

3. 关键点方向分配

统计以关键点为原点，利用所有在此邻域窗口内像素点的梯度形成一个方向直方图。梯度直方图将0~360度的方向范围分为36个柱，每柱10度。直方图的横坐标是梯度方向，共 36 项，每项代表了 10 度的范围；纵坐标是梯度大小，对于归到横坐标上任一项内所有的点，将其梯度大小相加，其和作为纵坐标。直方图最大值为关键点的主方向，大于主方向80%方向作为关键点辅方向。梯度的幅值和方向如下：
$m(x,y)=\sqrt{(L(x+1,y)-L(x-1,y){)}^2+(L(x,y+1),L(x,y-1){)}^2}$
$\theta (x,y)=ta{n}^{-1}((L(x,y+1)-L(x,y-1)/L(x+1,y)-L(x-1,y))$

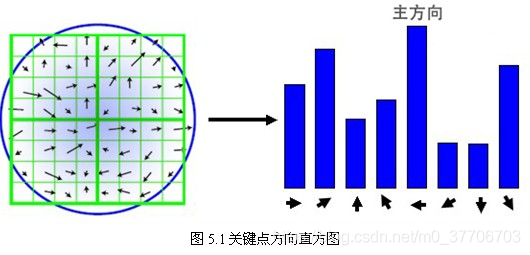
4. 关键点特征描述

使用在关键点尺度空间内4x4窗口计算8个方向的梯度信息，共4x4x8=128维向量将关键点表达出来。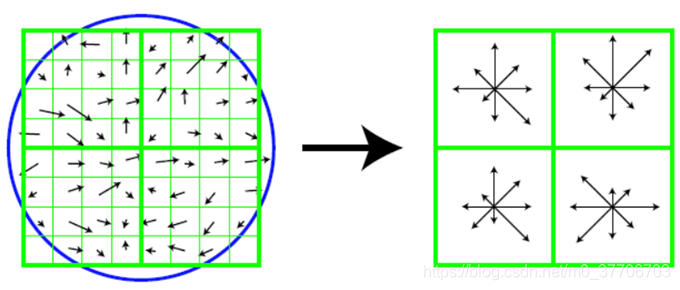

左侧图片为在关键点周围取一个88邻域，每一个小格都代表了特征点邻域所在的尺度空间的一个像素，箭头方向代表了像素梯度方向，箭头长度代表该像素的幅值。
右侧图片为四分之一个邻域，由4个大小22的像素区域组成，每个子区域生成一个八方向的梯度直方图，绘制每个梯度方向的累加可形成一个种子点。
这样一个特征点由4*4个种子点的信息所组成，如下图所示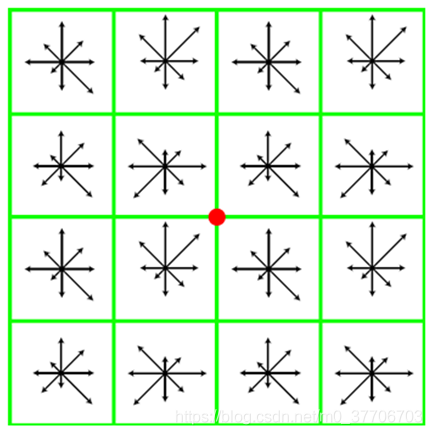

参考博客

https://blog.csdn.net/jinshengtao/article/details/50167533
https://blog.csdn.net/zddblog/article/details/7521424