
非线性方程使用简单迭代、牛顿、弦割
方程组使用牛顿、弦割、布罗伊登
import sympy
import numpy as np
import matplotlib.pyplot as plt
from sympy import *
def Nonlinear_equation_value(x): #计算非线性方程的值
value = (x**6)-5*(x**5)+3*(x**4)+(x**3)-7*(x**2)+7*x-20
return value
def simple_iteration(x0,alpha): #简单迭代法
print('------Using simple iteration------')
#print('iteration_times:', 1)
list_x = [] # 画图
x_next = ((x0**6) + 20) / ((2*(x0**5)) - 5*(x0**4) + 3*(x0**3) + (x0**2) - (7*x0) + 7)
list_x.append(x_next) # 画图 加入第一次计算的x
error = abs(Nonlinear_equation_value(x_next))
list_count = [] # 画图
k = 1
list_count.append(k) # 画图 加入第一次迭代计数
while(error>=alpha):
k += 1
list_count.append(k) # 画图 加入第2~N次迭代计数
#print('iteration_times:', k)
x_next = ((x_next**6) + 20) / ((2*(x_next**5)) - 5*(x_next**4) + 3*(x_next**3) + (x_next**2) - (7*x_next) + 7)
list_x.append(x_next) # 画图 加入第2~N次计算的x
error = abs(Nonlinear_equation_value(x_next))
#print('x',x_next)
print('total_iteration_times:', k)
print('error',error)
print('x*=',x_next)
plt.plot(list_count, list_x,"-o",color = 'red')
plt.show()
def Newton_iteration(x0,alpha):
print('------Using Newton iteration------')
list_x = [] # 画图
x_next = x0 - (Nonlinear_equation_value(x0) / (6*(x0 ** 5) - 25* (x0 ** 4) + 12*(x0 ** 3) + 3*(x0 ** 2) - 14*x0 + 7))
list_x.append(x_next) # 画图 加入第一次计算的x
error = abs(Nonlinear_equation_value(x_next))
list_count = [] # 画图
k = 1
list_count.append(k) # 画图 加入第一次迭代计数
while (error >= alpha):
k += 1
list_count.append(k) # 画图 加入第2~N次迭代计数
#print('iteration_times:', k)
x_next = x_next - (Nonlinear_equation_value(x_next) / (6*(x_next ** 5) - 25* (x_next ** 4) + 12*(x_next ** 3) + 3*(x_next ** 2) - 14*x_next + 7))
list_x.append(x_next) # 画图 加入第2~N次计算的x
error = abs(Nonlinear_equation_value(x_next))
print('total_iteration_times:', k)
print('error', error)
print('x*=', x_next)
plt.plot(list_count, list_x,"-o",color = 'red')
plt.show()
def String_cutting_iteration(x0,alpha):
print('------Using String cutting iteration------')
list_x = [] # 画图
x1 = ((x0**6) + 20) / ((2*(x0**5)) - 5*(x0**4) + 3*(x0**3) + (x0**2) - (7*x0) + 7) #使用简单迭代法获得x1
list_x.append(x1) # 画图 加入第一次计算的x
list_count = [] # 画图
list_count.append(1)
x_next = x1 - ((Nonlinear_equation_value(x1) * (x1 - x0)) / (Nonlinear_equation_value(x1) - Nonlinear_equation_value(x0)))
list_x.append(x_next) # 画图 加入第二次计算的x
error = abs(Nonlinear_equation_value(x_next))
k = 2
list_count.append(k)
while (error >= alpha):
k += 1
list_count.append(k)
#print('iteration_times:', k)
x1 = x_next
x_next = x1 - ((Nonlinear_equation_value(x1) * (x1 - x0)) / (Nonlinear_equation_value(x1) - Nonlinear_equation_value(x0)))
list_x.append(x_next)
error = abs(Nonlinear_equation_value(x_next))
print('total_iteration_times:', k)
print('error', error)
print('x*=', x_next)
plt.plot(list_count, list_x, "-o", color='red')
plt.show()
def Nonlinear_equation_sets_value(x0):
x0 = np.transpose(x0)
f = np.zeros(shape=(3, 1)) # 构造矩阵f
f_row0 = [x0[0,0]**2 + x0[0,1]**2 + x0[0,2]**2 - 1] # 每行重置空row
f_row1 = [2 * x0[0,0]**2 + x0[0,1]**2 -4*x0[0,2]]
f_row2 = [3 * x0[0,0]**2 + -4 * x0[0,1]**2 + x0[0,2]**2]
f[0] = f_row0
f[1] = f_row1
f[2] = f_row2
value = f
#print('v',value)
return value
def Newton(x0,alpha):
print('------Using Newton solve sets------')
J = np.zeros(shape=(3, 3)) #构造矩阵J
J_row0 = [2*x0[0,0],2*x0[1,0],2*x0[2,0]] # 每行重置空row
J_row1 = [4*x0[0,0],2*x0[1,0],-4]
J_row2 = [6*x0[0,0],-8*x0[1,0],2*x0[2,0]]
J[0] = J_row0
J[1] = J_row1
J[2] = J_row2
x_next = np.linalg.solve(J,-Nonlinear_equation_sets_value(x0)) + x0
value = Nonlinear_equation_sets_value(x_next)
error = ((value[0,0])**2 +(value[1,0])**2 +(value[2,0])**2 ) ** (1/2)
k = 1
while(error >= alpha):
k += 1
J = np.zeros(shape=(3, 3)) # 构造矩阵J
J_row0 = [2 * x_next[0, 0], 2 * x_next[1, 0], 2 * x_next[2, 0]] # 每行重置空row
J_row1 = [4 * x_next[0, 0], 2 * x_next[1, 0], -4]
J_row2 = [6 * x_next[0, 0], -8 * x_next[1, 0], 2 * x_next[2, 0]]
J[0] = J_row0
J[1] = J_row1
J[2] = J_row2
x_next = np.linalg.solve(J,-Nonlinear_equation_sets_value(x_next)) + x_next
value = Nonlinear_equation_sets_value(x_next)
error = ((value[0, 0]) ** 2 + (value[1, 0]) ** 2 + (value[2, 0]) ** 2) ** (1 / 2)
print('total_iteration_times:', k)
print('error', error)
print('x*=', x_next)
def String(x0,alpha):
print('------Using String solve sets------')
e1 = np.array([[1.0],[0.0],[0.0]])
e2 = np.array([[0.0], [1.0], [0.0]])
e3 = np.array([[0.0], [0.0], [1.0]])
h = 1 #h越大,迭代次数越多
J = np.zeros(shape=(3, 3)) # 构造矩阵J
J_row0 = [((x0[0, 0]+e1[0, 0]*h)**2 - x0[0, 0]**2)/h , ((x0[1, 0]+e2[1, 0]*h)**2 - x0[1, 0]**2)/h, ((x0[2, 0]+e3[2, 0]*h)**2 - x0[2, 0]**2)/h] # 每行重置空row
J_row1 = [(2 * ((x0[0, 0]+e1[0, 0]*h)**2 - x0[0, 0]**2))/h , ((x0[1, 0]+e2[1, 0]*h)**2 - x0[1, 0]**2)/h, (-4 * e3[2, 0]*h)/h]
J_row2 = [(3 * ((x0[0, 0]+e1[0, 0]*h)**2 - x0[0, 0]**2))/h, (-4 * ((x0[1, 0]+e2[1, 0]*h)**2 - x0[1, 0]**2))/h, ((x0[2, 0]+e3[2, 0]*h)**2 - x0[2, 0]**2)/h]
J[0] = J_row0
J[1] = J_row1
J[2] = J_row2
x_next = np.linalg.solve(J ,-Nonlinear_equation_sets_value(x0)) + x0
value = Nonlinear_equation_sets_value(x_next)
error = ((value[0,0])**2 +(value[1,0])**2 +(value[2,0])**2 ) ** (1/2)
k = 1
while(error >= alpha):
k += 1
J = np.zeros(shape=(3, 3)) # 构造矩阵J,求偏导改为计算差商
J_row0 = [((x_next[0, 0] + e1[0, 0] * h) ** 2 - x_next[0, 0] ** 2) / h,
((x_next[1, 0] + e2[1, 0] * h) ** 2 - x_next[1, 0] ** 2) / h,
((x_next[2, 0] + e3[2, 0] * h) ** 2 - x_next[2, 0] ** 2) / h] # 每行重置空row
J_row1 = [(2 * ((x_next[0, 0] + e2[0, 0] * h) ** 2 - x_next[0, 0] ** 2)) / h,
((x_next[1, 0] + e2[1, 0] * h) ** 2 - x_next[1, 0] ** 2) / h, (-4 * e3[2, 0] * h) / h]
J_row2 = [(3 * ((x_next[0, 0] + e1[0, 0] * h) ** 2 - x_next[0, 0] ** 2)) / h,
(-4 * ((x_next[1, 0] + e2[1, 0] * h) ** 2 - x_next[1, 0] ** 2)) / h,
((x_next[2, 0] + e3[2, 0] * h) ** 2 - x_next[2, 0] ** 2) / h]
J[0] = J_row0
J[1] = J_row1
J[2] = J_row2
x_next = np.linalg.solve(J ,-Nonlinear_equation_sets_value(x_next)) + x_next
value = Nonlinear_equation_sets_value(x_next)
error = ((value[0, 0]) ** 2 + (value[1, 0]) ** 2 + (value[2, 0]) ** 2) ** (1 / 2)
print('total_iteration_times:', k)
print('error', error)
print('x*=', x_next)
def Broyden(x0,alpha):
print('------Using Broyden solve sets------')
J = np.zeros(shape=(3, 3)) # 构造矩阵J
J_row0 = [2 * x0[0, 0], 2 * x0[1, 0], 2 * x0[2, 0]] # 每行重置空row
J_row1 = [4 * x0[0, 0], 2 * x0[1, 0], -4]
J_row2 = [6 * x0[0, 0], -8 * x0[1, 0], 2 * x0[2, 0]]
J[0] = J_row0
J[1] = J_row1
J[2] = J_row2
A = J
A_inv = np.linalg.inv(A)
x_next = x0 - np.dot(A_inv,Nonlinear_equation_sets_value(x0))
value = Nonlinear_equation_sets_value(x_next)
error = ((value[0, 0]) ** 2 + (value[1, 0]) ** 2 + (value[2, 0]) ** 2) ** (1 / 2)
k = 1
while (error >= alpha):
k += 1
s = x_next - x0
y = Nonlinear_equation_sets_value(x_next) - Nonlinear_equation_sets_value(x0)
A_inv = A_inv + ((np.dot(np.dot((s - np.dot(A_inv,y)),np.transpose(s)),A_inv)) / np.dot(np.dot(np.transpose(s),A_inv),y))
x_next = x_next - np.dot(A_inv,Nonlinear_equation_sets_value(x_next))
value = Nonlinear_equation_sets_value(x_next)
error = ((value[0, 0]) ** 2 + (value[1, 0]) ** 2 + (value[2, 0]) ** 2) ** (1 / 2)
print('total_iteration_times:', k)
print('error', error)
print('x*=', x_next)
if __name__ == '__main__': #使用P228的Steffensen方法
alpha = 1e-8
x0 = np.array([[1.0],[1.0],[1.0]]) #非线性方程组的初值
Newton(x0,alpha) #牛顿法解非线性方程组
String(x0,alpha) #弦割法解非线性方程组
Broyden(x0,alpha) #布罗依登法解非线性方程组
'''
通过二分法确定解属于[4.25,4.34375]
'''
simple_iteration(4.25, alpha) #简单迭代法解非线性方程,初值为4.25
Newton_iteration(4.25, alpha) #牛顿法解线性方程
String_cutting_iteration(4.25,alpha) #牛顿法解线性方程
simple_iteration(4.34375, alpha) #简单迭代法解非线性方程,初值为4.34375
Newton_iteration(4.34375, alpha) #牛顿法解线性方程
String_cutting_iteration(4.34375,alpha) #牛顿法解线性方程
运行结果
C:\Anaconda\envs\pythonProject\python.exe C:/Users/871674389/PycharmProjects/pythonProject/Iteration.py
------Using Newton solve sets------
total_iteration_times: 5
error 4.888843483876897e-16
x*= [[0.69828861]
[0.6285243 ]
[0.34256419]]
------Using String solve sets------
total_iteration_times: 27
error 8.608313761523177e-09
x*= [[0.69828861]
[0.6285243 ]
[0.34256419]]
------Using Broyden solve sets------
total_iteration_times: 18
error 5.976752082256246e-09
x*= [[0.69828861]
[0.6285243 ]
[0.34256419]]
------Using simple iteration------
total_iteration_times: 12
error 2.4398936204761412e-09
x*= 4.333755446918165
------Using Newton iteration------
total_iteration_times: 4
error 2.984279490192421e-13
x*= 4.333755446919994
------Using String cutting iteration------
total_iteration_times: 11
error 2.0288908331167477e-09
x*= 4.333755446918473
------Using simple iteration------
total_iteration_times: 11
error 2.5482194132564473e-09
x*= 4.333755446921907
------Using Newton iteration------
total_iteration_times: 3
error 6.181721801112872e-13
x*= 4.333755446919995
------Using String cutting iteration------
total_iteration_times: 6
error 3.779234702960821e-10
x*= 4.333755446920279
Process finished with exit code 0
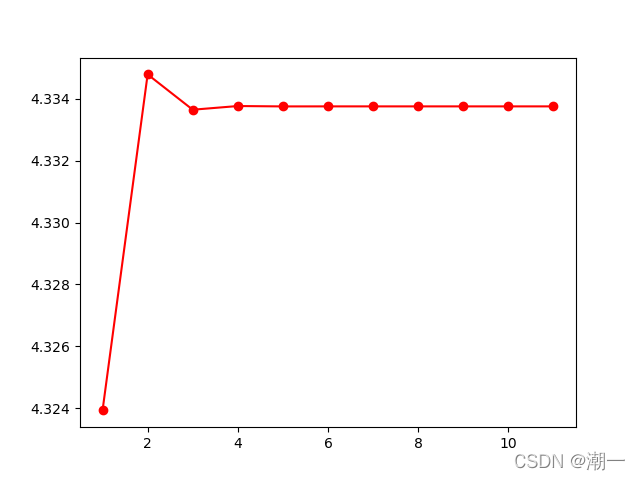
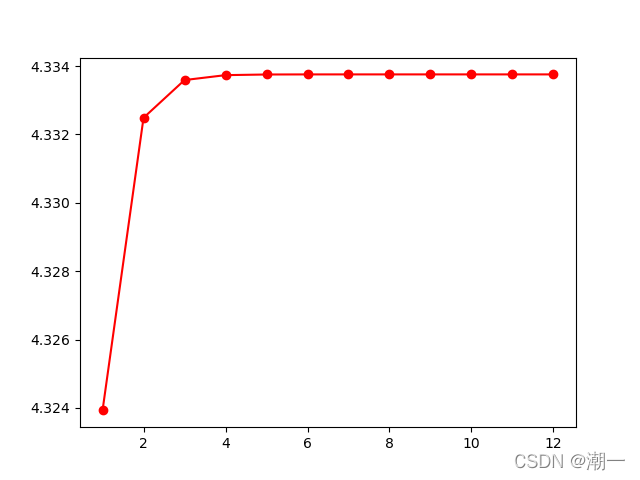
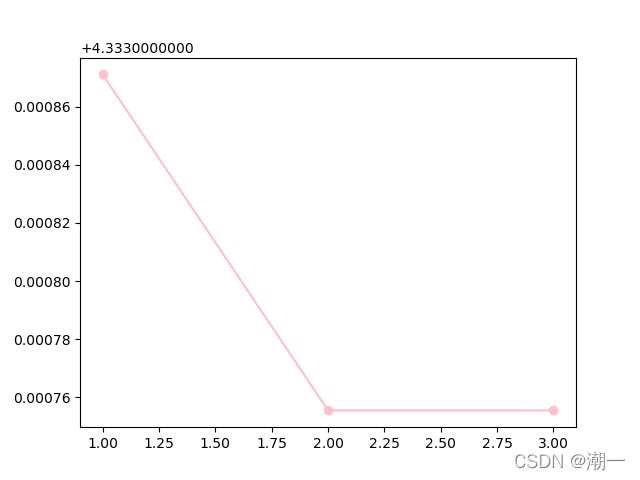
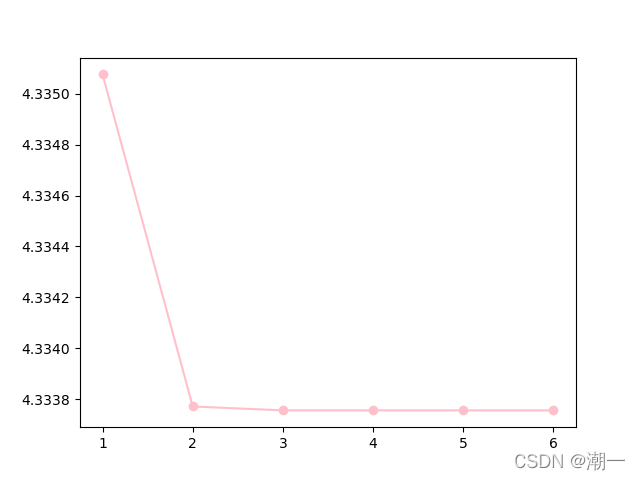
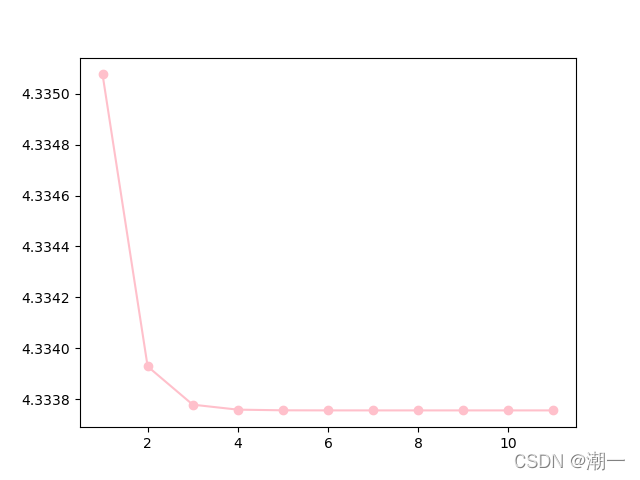
非线性方程绘图(依次是简单迭代、牛顿、弦割)
粉色和红色表示分别从解的区间的下界4.25和上界4.34375趋近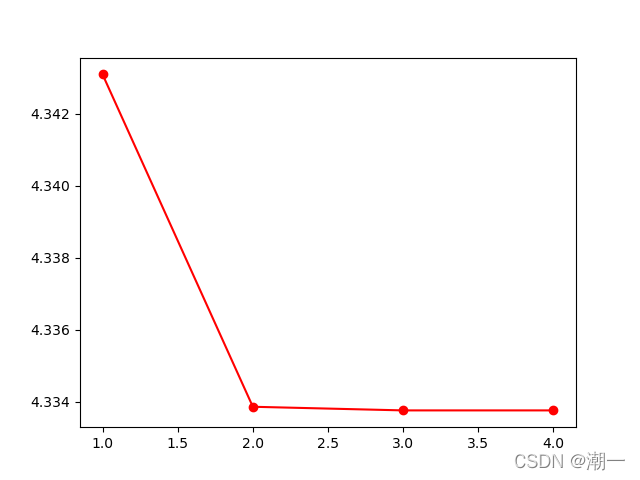
版权声明:本文为qq_41821608原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。