Persformer

参考文献 Persformer: A Transformer Architecture for Topological Machine Learning

这是一篇使用拓扑方法的 Transformer. 输入是 持续图, 输出是分类概率.

拓扑数据分析的简单流程

$\mathbb{Z}/2$-系数的 单纯同调

拓扑同调理论最简单的部分, 其各维同调群反应空间情况为:
0-维同调群 ${\text{H}}_0$, 空间连通分支的个数, 用于聚类.

1-维同调群 ${\text{H}}_1$, 空间含圆圈的数目.

2-维同调群 ${\text{H}}_2$, 空间含空心球的数目.
$$⋮$$
n-维同调群 ${\text{H}}_n$, 空间 n-维洞的数目.

持续同调理论

输入点云(空间中的一堆有距离的点), 使用 实数 r 建立$\mathbb{Z}/2$-系数的 单纯复形 $C^r$, 由此得到持续同调.

每个 $C^r$ 产生单纯同调群 ${\text{H}}_i^r$. i 为r 处同调群的维数, 每个同调群都有生成元. $r_1\le r_2$, 有自然的包含映射 $i^{r_1\to r_2}:C^{r_1}\to C^{r_2}$, 诱导出同调群之间的映射 $i_{\ast }^{r_1\to r_2}:{\text{H}}^{r_1}\to {\text{H}}^{r_2}$. 此处 $i_{\ast }$ 为 0 或 1.
对 $r_1$中的生成元 $a$, d:=$\text{min}\{r_2:i_{\ast }^{r_1\to r_2}(a)=0\}$, d为 a 的死亡时刻. b:=$\text{min}\{r_0:i_{\ast }^{r_0\to r_1}(e)=a,e\in {\text{H}}^{r_0}\}$, b 为 a 的出生时刻. 由于 $i_{\ast }$ 的取值特点, e=a. 即, 将 不同 r 处的 a 看成是同一a 在不同时刻下的表现, 点 (b,d) 记录这个 元素(洞)的出生和死亡时刻.

于是每个洞都可以映射到一个实平面上的点(b,d) 这个图称作持续图.
也可以映射为 (b,d-b), b 为出生时刻, b-d 为存活时间, 此称作条形码.
$需要注意的是持续图或者条形码都是使用同一维数的洞画的,也即是有多少同调维数就有多少持续图或者条形码.$

**做一点注记. 拓扑只是关注整体性质的, 例如腔洞的数目, 但是持续同调理论还能够捕获到曲率这个局部的信息. 这意味着持续同调能够用于蛋白质结构-功能预测, 材料科学.

向量化

不论是持续图还是条形码, 都不是向量. 为了能够在机器学习中使用拓扑特征, 需要将 持续图或者条形码向量化.

目前有两种思路, 其一是手动向量化, 即寻找合适的核映射将持续同调的输出映射到 希尔伯特空间, bin 方法, 持续景观等; 另一种是使用机器学习学习出向量, 例如 Perslayer, Performer.

机器学习

有了向量就可以使用机器学习算法分析.

Persformer

Perrformer 的输入是持续图, 输出是分类任务. 如前文所述, Persformer 将 持续图的向量化看成是可学习的参数.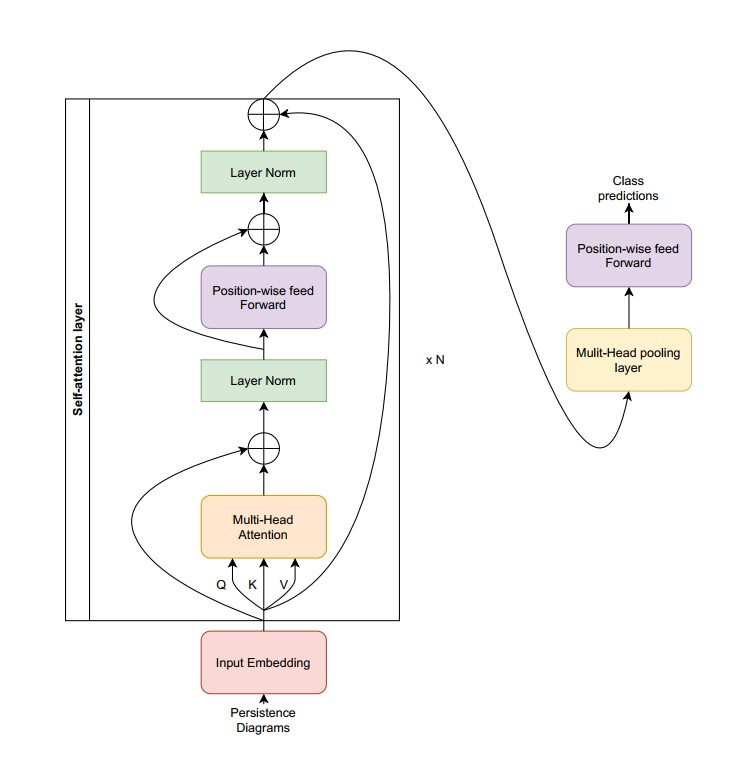

首先是自注意力层, 和正常的自注意力层比较, Persformer 没有考虑位置信息, 在输出处 增加了残差连接层. 这是因为 持续图没有序关系. 残差层是避免梯度消失.
解码块没有, 取而代之的是 多头池化层, FF层.

重点解释一下多头池化层.

多头池化层是多头注意力层的变种, 其 query 是需要一个学习的参量 $Q\in {\mathbb{R}}^{1\times d}$. key 和 value 向量来自于自注意力层输出 $z\in {\mathbb{R}}^{n\times d}$ 的线性变换 $\text{rFF}(z)$. $\text{rFF}$ 是逐 $行向量$ 前馈神经网络.即
$$\text{MultiHead}(Q,\text{rFF}(z),\text{rFF}(z))$$

需要注意到 由于没有位置信息的输入, 这个模型没有考虑序关系, 所以不太适合于需要序关系的应用场景.

Persformer 有多好

满足特定的万有逼近定理, 仅仅对 Hausdorff-连续 实值函数有关.

持续图中点的轻重

持续图中的点 (b,d), $b<d$. 于是点 (b,d) 位于直线$y=x$ 的上方. 距离这个直线近的点存活的时间短, 人们开始认为这样的点(短码)在数据分析中仅仅是噪音. 那么我们会去问怎么区分噪音和非噪音?
针对分类问题, Persformer 可以看成是几乎处处可微分的函数 $\text{F}:\mathcal{D}\to {\mathbb{R}}^m$. $\mathcal{D}$ 是持续图空间, 一个持续图记作
$$x:=\{x_i\in {\mathbb{R}}^{2+d}{\}}_{i\in \{1,2,\cdots n\}},$$
$x_i$ 的前 2 个分量是 (b,d), 后 d 个分量是 判断 $x_i$ 所在的同调维数, 使用 独热编码($(0100\cdots 0)$代表1维同调中生成元). m 是分类数目. 这个映射将 一个持续图映射为 分类概率的对数. 同调维数是无穷的, 文中假定需要考虑的最高维数为 d.
$\text{F}$ 的显著图被定义为
$${\text{S}}_F(x):=(||\frac{\partial {\text{F}}_{i(x)}}{\partial x_k}|{|}_2)\in {\mathbb{R}}^n,$$
其中 $i(x):={\text{argmax}}_j\{\text{F}(x{)}_j\}$.

这样 显著图指出了持续图中每个点在 分类中的重要程度.

实例表明 短码也有可能在分类任务中起重要作用.