介绍
Intelligent Reflecting Surface-Aided Wireless Communications: A Tutorial文章的整理。
- IRS基础部分及建模
- IRS优化
- IRS信道估计
- IRS部署
- 拓展
IRS介绍
IRS: Intelligent reflecting surface
背景
- 6G存在的需求,例如超高数据速率和能源效率,极高的可靠性和低延迟等
- 解决来自用户的时变无线信道
什么是IRS
Generally speaking, IRS is a planar surface comprising a large number of passive reflecting elements, each of which is able to induce a controllable amplitude and/or phase change to the incident signal independently
- IRS elements 是无源的(虽然后面会讲到还是需要一定的能源(用来调整幅度反射和相位反射),但是相比其他设备,这些能源是微乎其微的,还是可以认为是无源的)
IRS作用及优势
从概念上:
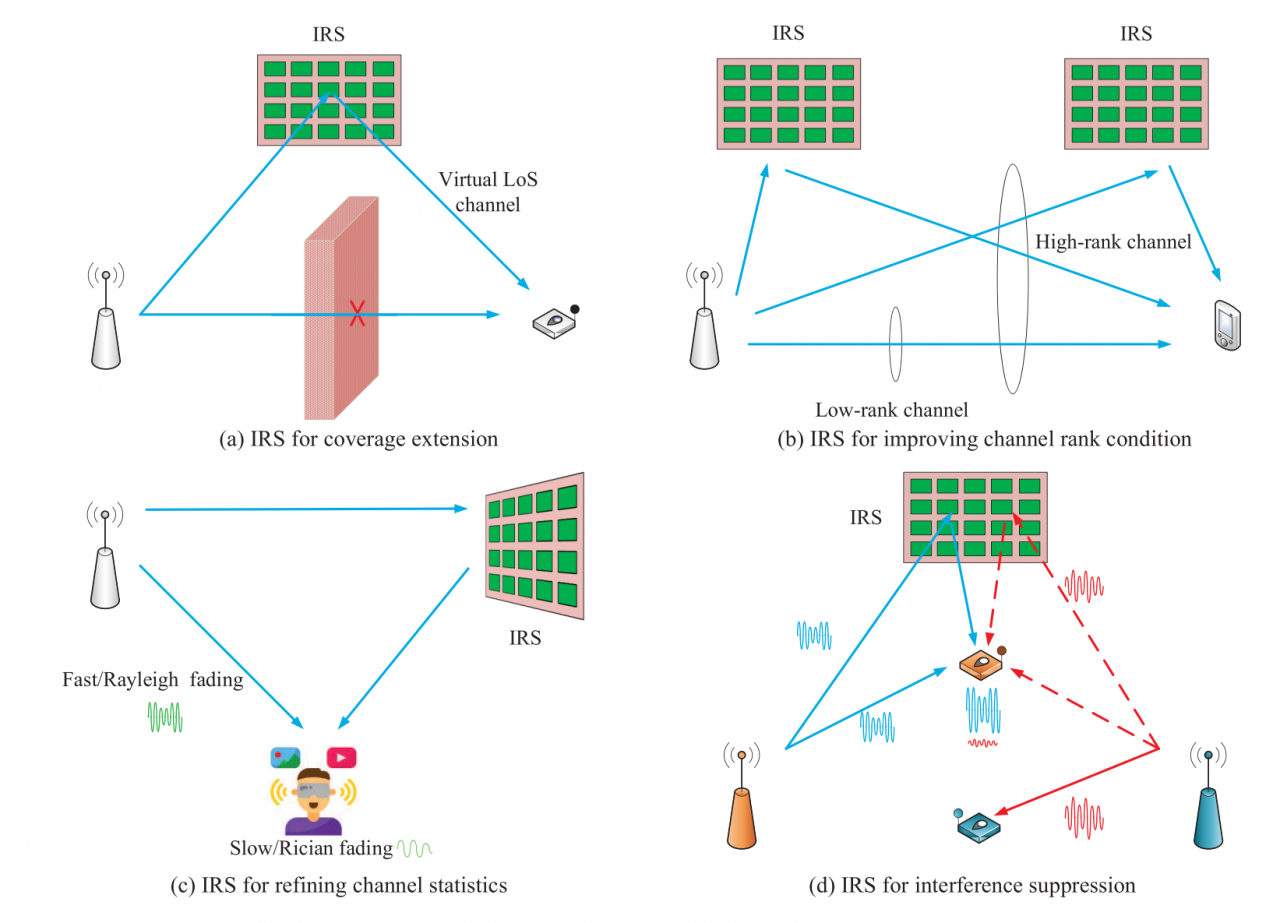
- (a): 创建虚拟视距(LoS)链接以通过智能反射面绕过收发器之间的障碍物
- (b): 在期望的方向添加额外的信号路径以提升信道等级条件
- ©: 改善信道分布,例如将瑞利/快衰落转换为Rician/慢衰落以实现超高可靠性
- (d): 抑制一些干扰
在实施上
- 因为是无缘的(仅被动反射信号),所以不需要任何发射射频反射链,硬件要求低(与传统有源中继相比)。
- 全双工工作模式,没有任何天线噪声放大和自干扰。
- 安装拆除简单
- 极大的灵活性和与现有无线系统的兼容性
IRS挑战
- 无源反射原件需要适当设计,实现IRS element之间的协同信号聚焦或干扰消除。考虑与基站、用户的传输联合设计。
- 由于IRS没有发射射频链,所以要考虑如何获得IRS与其用户之间的信道状态信息。
- IRS在无线网络中最大化网络容量的最佳部署策略需要重新设计。
IRS建模
以x ( t ) x(t)x(t)表示等效复值基带发射信号,对于一个有N NN个反射单元的IRS,以n nn代表单元,即n ∈ { 1 , ⋯ , N } n\in\{1, \cdots, N\}n∈{1,⋯,N},用α 1 , n e − j ξ 1 , n \alpha_{1, n}e^{-j\xi_{1, n}}α1,ne−jξ1,n表示基带信号从发射机到IRS的反射单元n nn的复信道系数,其中α 1 , n \alpha_{1, n}α1,n表示幅度衰减(amplitude attenuation),e − j ξ 1 , n e^{-j\xi_{1,n}}e−jξ1,n表示窄带系统平坦信道的相移。所以其带通信号(经过上变频)可以表示为:
y i n , n ( t ) = R e { α 1 , n e − j ξ 1 , n x ( t ) e j 2 π f c t } y_{in,n}(t)=Re\{\alpha_{1, n}e^{-j\xi_{1, n}}x(t)e^{j2\pi f_ct}\}yin,n(t)=Re{α1,ne−jξ1,nx(t)ej2πfct}
其中,f c f_cfc是载波频率;该单元(第n nn个单元)的幅度衰减和时间延迟分别用β n ∈ [ 0 , 1 ] \beta_n\in[0, 1]βn∈[0,1](因为是无源的)和t n ∈ [ 0 , 1 / f c ] t_n\in[0, 1/f_c]tn∈[0,1/fc]表示。忽略电路非线性和相位噪声等硬件缺陷,IRS单元n nn的反射信号表示为:
y o u t , n ( t ) = β n y i n , n ( t − t n ) = R e { β n α 1 , n e − j ξ 1 , n x ( t − t n ) e j 2 π f c ( t − t n ) } ≈ R e { [ β n e − j θ n ′ α 1 , n e − j ξ 1 , n x ( t ) ] e j 2 π f c t } \begin{aligned} y_{out,n}(t)&=\beta_ny_{in,n}(t-t_n)\\ &=Re\{\beta_n\alpha_{1,n}e^{-j\xi_{1,n}}x(t-t_n)e^{j2\pi f_c(t-t_n)}\} \\&\approx Re\{[\beta_ne^{-j\theta^{'}_n}\alpha_{1,n}e^{-j\xi_{1,n}}x(t)]e^{j2\pi f_ct}\} \end{aligned}yout,n(t)=βnyin,n(t−tn)=Re{βnα1,ne−jξ1,nx(t−tn)ej2πfc(t−tn)}≈Re{[βne−jθn′α1,ne−jξ1,nx(t)]ej2πfct}
其中,在t n ≤ 1 / f c ≪ 1 / B t_n\leq1/f_c\ll1/Btn≤1/fc≪1/B的前提下,假设x ( t − t n ) ≈ x ( t ) x(t-t_n)\approx x(t)x(t−tn)≈x(t);并有− θ n ′ ≜ − 2 π f c t n ∈ [ − 2 π , 0 ] -\theta_n^{'}\triangleq-2\pi f_ct_n\in[-2\pi,0]−θn′≜−2πfctn∈[−2π,0]是单元n nn引起的相移。由s i n , n ( t ) ≜ α 1 , n e − j ξ 1 , n x ( t ) s_{in,n}(t)\triangleq \alpha_{1, n}e^{-j\xi_{1, n}}x(t)sin,n(t)≜α1,ne−jξ1,nx(t)并且有s o u t , n ≜ β n e − j θ n ′ α 1 , n e − j ξ 1 , n x ( t ) s_{out,n}\triangleq\beta_ne^{-j\theta^{'}_n}\alpha_{1,n}e^{-j\xi_{1,n}}x(t)sout,n≜βne−jθn′α1,ne−jξ1,nx(t)$
进一步,由于θ n ′ \theta^{'}_nθn′是以2 π 2\pi2π为周期的,所以为方便后续部分,取θ n ∈ [ 0 , 2 π ] \theta_n\in [0,2\pi]θn∈[0,2π],有:
s o u t , n ( t ) = β n e − j θ n ′ s i n , n ( t ) = β n e j θ n s i n , n ( t ) \begin{aligned} s_{out,n}(t)=\beta_ne^{-j\theta^{'}_n}s_{in,n}(t)=\beta_ne^{j\theta_n}s_{in,n}(t) \end{aligned}sout,n(t)=βne−jθn′sin,n(t)=βnejθnsin,n(t)
所以在基带信号模型中,IRS单元n nn的输出/反射信号是通过将相应的输入/入射信号乘以复反射系数β n e − j θ n \beta_ne^{-j\theta_n}βne−jθn得到的。
再接上从IRS单元n nn到接收端的信号(与前面相似的等效窄带平坦频率信道),则有接收端的表达式:
y r , n ( t ) = R e { [ α 1 , n e − j ξ 1 , n β n e j θ n α 2 , n e − j ξ 2 , n x ( t ) ] e j 2 π f c t } \begin{aligned} y_{r,n}(t)=Re\{[\alpha_{1,n}e^{-j\xi_{1,n}}\beta_ne^{j\theta_n}\alpha_{2,n}e^{-j\xi_{2,n}}x(t)]e^{j2\pi f_ct}\} \end{aligned}yr,n(t)=Re{[α1,ne−jξ1,nβnejθnα2,ne−jξ2,nx(t)]ej2πfct}
用h r , n ∗ ≜ α 1 , n e − j ξ 1 , n h^*_{r,n}\triangleq\alpha_{1,n}e^{-j\xi_{1,n}}hr,n∗≜α1,ne−jξ1,n(发射端到IRS的信道),并用g n ≜ α 2 , n e − j ξ 2 , n g_n\triangleq\alpha_{2,n}e^{-j\xi_{2,n}}gn≜α2,ne−jξ2,n(IRS到接收端的信道),上式变为:
y n ( t ) = β n e j θ n h r , n ∗ g n x ( t ) \begin{aligned} y_n(t)=\beta_ne^{j\theta_n}h^*_{r,n}g_nx(t) \end{aligned}yn(t)=βnejθnhr,n∗gnx(t)
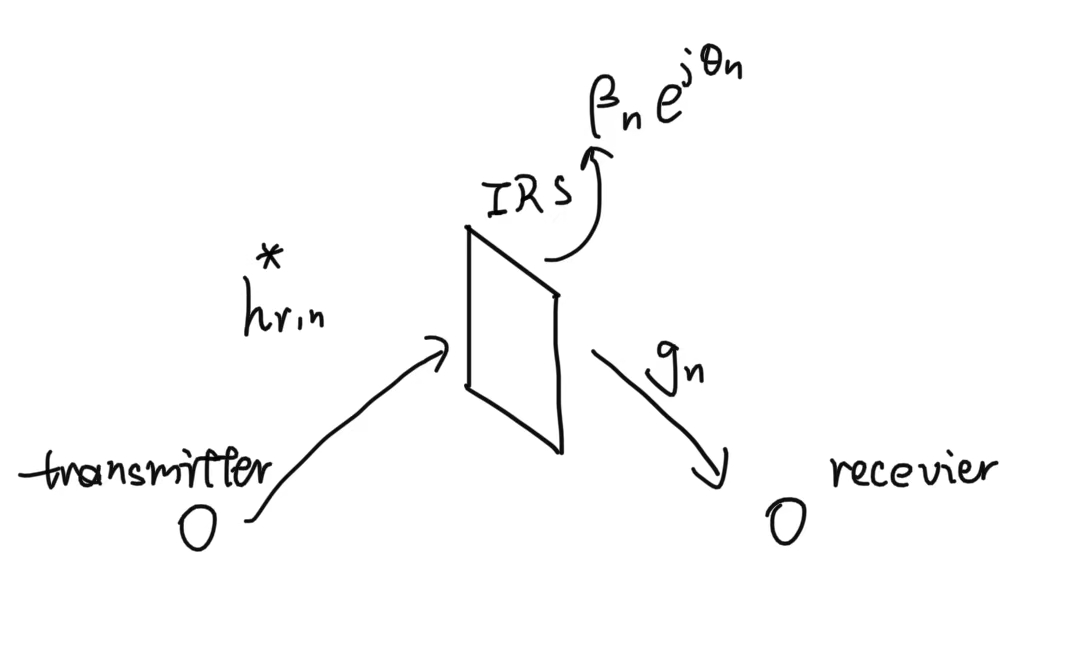
假设没有信号耦合,即所有IRS单元独立地反射入射信号。并忽略多次反射(因为路径损失较大),则有考虑N NN个单元时,有接收端:
y ( t ) = ( ∑ n = 1 N β n e j θ n h r , n ∗ g n ) x ( t ) = h r H Θ g x ( t ) \begin{aligned} y(t)=(\sum_{n=1}^N\beta_ne^{j\theta_n}h^*_{r,n}g_n)x(t)=\textbf{h}_r^H\Theta\textbf{g}x(t) \end{aligned}y(t)=(n=1∑Nβnejθnhr,n∗gn)x(t)=hrHΘgx(t)
其中h r H = [ h r , 1 ∗ , ⋯ , h r , N ∗ ] \textbf{h}_r^H=[h^*_{r, 1},\cdots,h^*_{r,N}]hrH=[hr,1∗,⋯,hr,N∗],g = [ g 1 , ⋯ , g N ] T \textbf{g}=[g_1,\cdots,g_N]^Tg=[g1,⋯,gN]T,Θ = d i a g ( β 1 e j θ 1 , ⋯ , β N e j θ N ) \Theta=diag(\beta_1e^{j\theta_1},\cdots,\beta_Ne^{j\theta_N})Θ=diag(β1ejθ1,⋯,βNejθN)因为每个IRS单元独立地反射信号,且没有信号耦合,所以Θ \ThetaΘ是对角阵。
IRS硬件实现
硬件结构
由于发射机、接收机以及周围物体的移动性,信道通常是时变的,因此需要基于信道变化的IRS实时可调。所以需要联网以进行自适应反射。
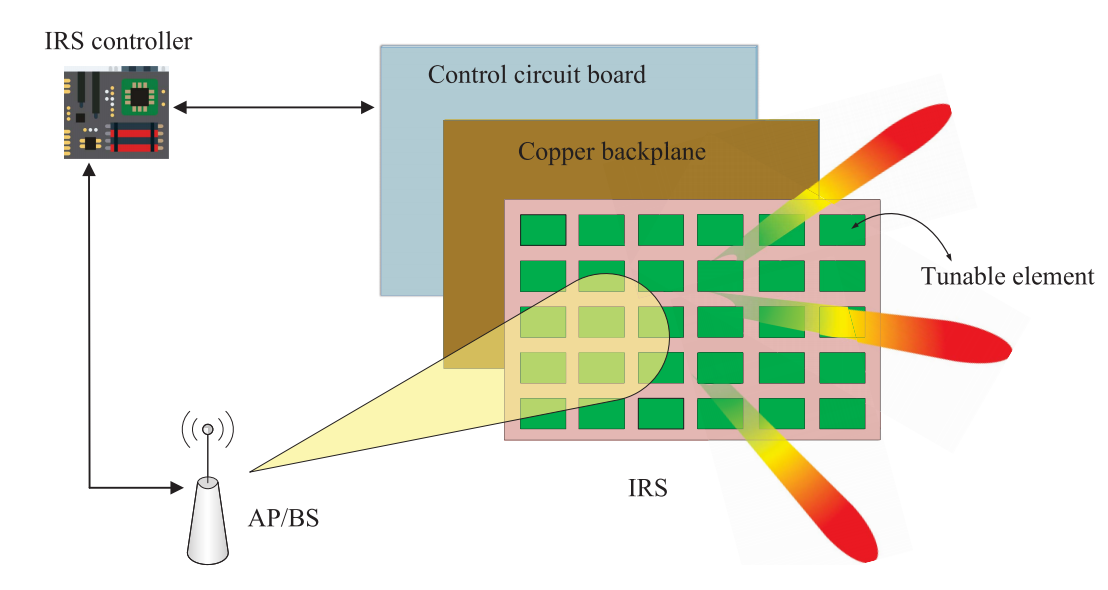
智能控制器,FPGA,总的控制端
第一层,调整层,控制层,也可以布置一些传感器(感知周围感兴趣的无线电信号,以方便智能控制器设计反射系数)
第二层,铜,减少信号能量损失
第三层,可调整的单元
为了实现重新配置IRS单元以实现高度可控反射,有三种主要方法被提出:
- 机械驱动(机械旋转、平移)
- 功能材料(液晶、石墨烯等)
- 电子设备(PIN二极管等)
第三种电子设备(PIN二极管等)是最常用的。
实际限制
离散的反射幅度和相移
用固定的PIN二极管,需要大数量才能控制精细相移,例如log 2 8 = 3 \log_28=3log28=3,即8级相移需要3个PIN二极管;使用变容二极管则需要更大范围的偏置电压,成本更高。
顺便提出了两个特殊结构:

耦合的反射幅度和相移
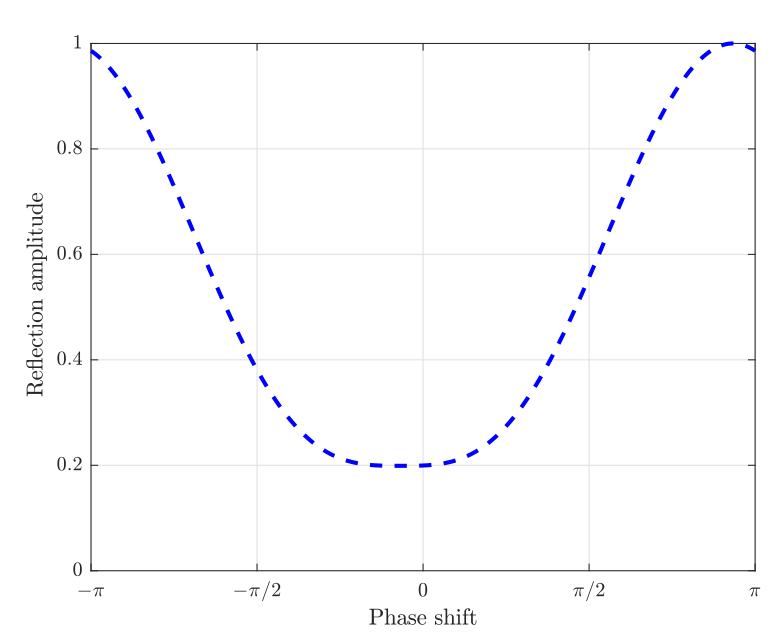
有人提出反射的幅度和相移之间存在非线性耦合,所以不能单独调节。
产生这种现象的原因是因为:0相移时,反射电流与单元电流同相(in-phase),电流强度增加,导致发热增多,反射幅度下降;当电流反相时(out-of-phase),电流强度减弱,发热变少,反射幅度增加。
此外,IRS理论上是无源的(passive),但是例如控制PIN二极管时,需要消耗一部分能量。只是说这部分能量相对较小。
其他相关内容及未来研究方向
- IRS单元之间的耦合目前是被忽略的。考虑在增大IRS单元密度以提高性能时,可能会使耦合更严重,以至于不能忽略。考虑耦合反射系数或者开发有效的去耦、隔离技术。
- 目前考虑的模型对信号的入射角不敏感。目前的部分实现证明IRS反射系数,特别是相移,对入射角非常敏感。同时这也意味着信道互易假设可能不再有效,即上行链路的信道估计不再适用于下行链路的信道估计,vice versa。
- 对于宽带信号的建模以及频率/时间偏移、相位噪声等。