① 将所有的顶点分为两部分:已知最短路程的顶点集合 P 和未知最短路径的顶点集合 Q。最开始,已知最短路径的顶点集合 P 中只有源点一个顶点。我们这里用一个 visited[i] 数组来记录哪些点在集合 P 中。例如对于某个顶点 i,如果 visited[i]为 true 则表示这个顶点在集合 P 中,如果 visited[i]为 false 则表示这个顶点在集合 Q 中。【初始化visited[i]标记】
② 设置源点 s 到自己的最短路径为 0 即 dis=0。若存在源点有能直接到达的顶点 i,则把 dis[i] 设为 e[s] [i] 。同时把所有其它(源点不能直接到达的)顶点的最短路径为设为 ∞ 。【初始化dis距离表】
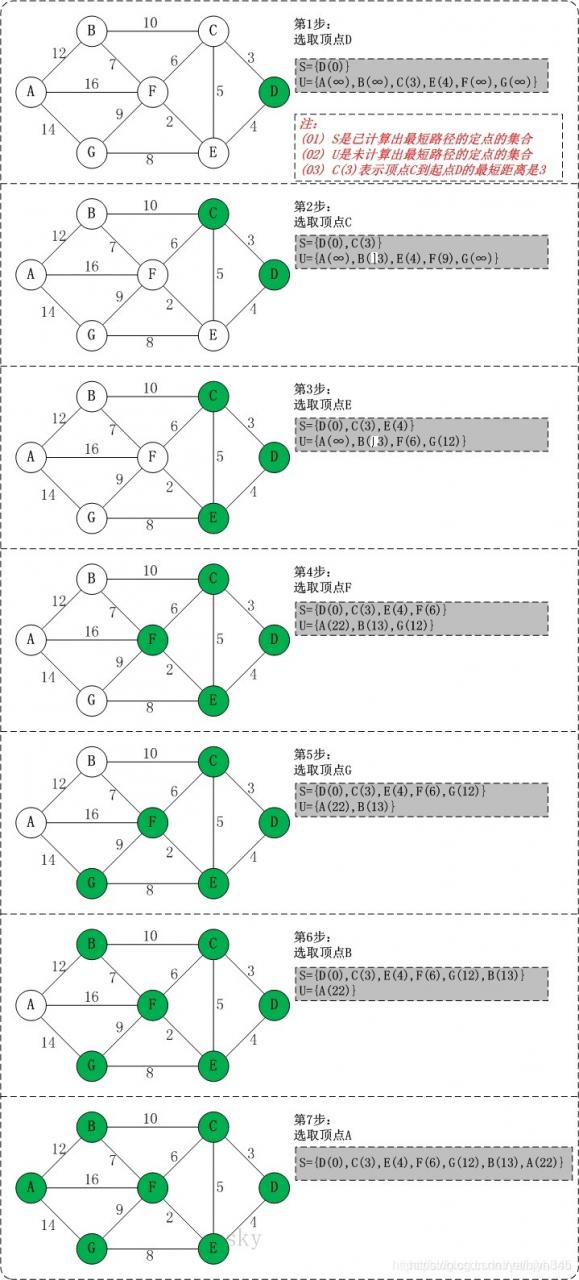
③ 在集合 Q 的所有顶点中选择一个离源点 s 最近的顶点 u(即 dis[u] 最小)加入到集合 P。并考察所有以点 u 为起点的边,对每一条边进行松弛操作。例如存在一条从 u 到 v 的边,那么可以通过将边 u->v 添加到尾部来拓展一条从 s 到 v 的路径,这条路径的长度是 dis[u]+e[u] [v]。如果这个值比目前已知的dis[v]的值要小,我们可以用新值来替代当前dis[v] 中的值。【取dis最小(访问过的除外),边松弛】【核心】
④ 重复第 ③ 步,如果集合 Q 为空,算法结束。最终 dis 数组中的值就是源点到所有顶点的最短路径。
作者:0与1的邂逅
链接:https://www.jianshu.com/p/8b3cdca55dc0
来源:简书