听不少大佬建议过——力扣刷题要从树开始 !
因为可以建立起套路化的思路~ 另外就是锻炼好递归的思想
所以 我们从树开始~
本专题采用前面提到的 “兔系刷题法” 不求钻研多种解法 只求快速见题型快速刷题!
另外 力扣评论区里看见的——
树的题目写不出来,多背几个模版就行。
前中后序、广度深度遍历、路径和、深度,直径,这些全部背下来。
感觉很有道理!多背些多理解些套路嘛!
本专题的套路较为冷门 为 二叉树的重建 数据结构中的重要知识点
真绕啊!
本次的两道题比前几期的都要烧脑嗷
虽然是我们数据结构都学到过的东西
但是真正让你实现 你真的有思路嘛?
本专题体会!
有的题目
画图真的很重要!!!
105. 从前序与中序遍历序列构造二叉树
根据一棵树的前序遍历与中序遍历构造二叉树。
注意:
你可以假设树中没有重复的元素。
例如,给出
前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]
返回如下的二叉树——
3
/ \
9 20
/ \
15 7
解题思路
参考威威哥的题解 实在是太清晰啦!
首先确定了使用分治法的思想进行解题
复习一下分治法的思想:把原问题拆解成若干个与原问题结构相同但规模更小的子问题,待子问题解决以后,原问题就得以解决,“归并排序”和“快速排序”都是分治法思想的应用,其中“归并排序”先无脑地“分”,在“合”的时候就麻烦一些;“快速排序”开始在 partition 上花了很多时间,即在“分”上使了很多劲,然后就递归处理下去就好了,没有在“合”上再花时间。
作者:liweiwei1419
链接:https://leetcode-cn.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal/solution/qian-xu-bian-li-python-dai-ma-java-dai-ma-by-liwei/
这段感觉说得实在太棒了!把之前的知识都串起来了!
疯狂打call!!
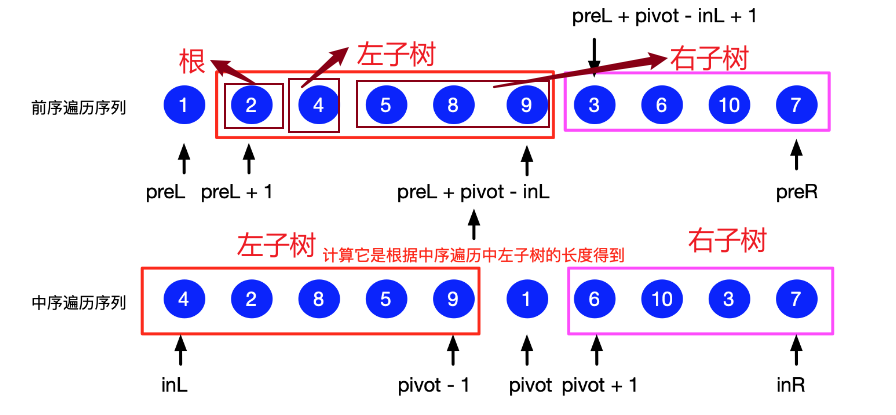
在本题中 首先要明确:
前序遍历数组的第一个数 为 二叉树根节点
在中序遍历中找到这个根节点 然后就可以将当前遍历到的那部分划分成——根 左子树 右子树
然后将每部分进行递归完成
分治法的思想体现在——
把数组逐渐划分为 根 左子树 右子树 这几个部分
另外这题的难点与关键是——
- 理解这一大堆参数
_buildTree中的这些参数!
//preorder 二叉树前序遍历输入数组 inorder 二叉树中序遍历输入数组
// preLeft 前序遍历左边界 preRight 前序遍历右边界
// inLeft 中序遍历左边界 inRight 中序遍历右边界
- 通过参数与参数的加减得到正确的边界值
下面看看威威哥画的题解 好理解些~
Java代码
class Solution {
//01 用下面这些元素构造二叉树 ——————
//输入数组preorder [preLeft, preRight]中的所有元素
//inorder [inLeft, inRight]中的所有元素
public TreeNode _buildTree(int[] preorder, int preLeft, int preRight, int[] inorder, int inLeft, int inRight){
// preorder 二叉树前序遍历输入数组 inorder 二叉树中序遍历输入数组
// preLeft 前序遍历左边界 preRight 前序遍历右边界
// inLeft 中序遍历左边界 inRight 中序遍历右边界
//1 设置退出条件~
if (preLeft > preRight || inLeft > inRight){
return null;
}
//2 确定先序遍历的起点元素 并找到这个值在中序输入数组中的位置 这个是最重要的地方!
int pivot = preorder[preLeft];//前序遍历输入数组的当前遍历到的左边界值pivot 这个点为起点元素~这是核心!是每一步的“根”!!
TreeNode root = new TreeNode(pivot);//root:当前遍历到的那个核心 每一步的“根”
int pivotIndex = inLeft;//初始化pivotIndex 从中序遍历输入数组上次的左边界开始找那个“根”
// 3 找到起点元素在中序遍历输入数组当前遍历到部分 的位置pivotIndex
// (最好再做一个判断 如果中序遍历输入数组当前左边界 大于 中序右边界 就退出 本解法没做)
while(inorder[pivotIndex] != pivot){
pivotIndex ++;
}
//4 上面终于绕明白了QAQ 进行快乐的递归~
//下面的部分看图解就一目了然了~
root.left = _buildTree(preorder, preLeft + 1, pivotIndex - inLeft + preLeft, inorder, inLeft, pivotIndex - 1);//构造左子树
// 前序数组中的[preLeft + 1, pivotIndex - inLeft + preLeft] 中序数组中的[inLeft, pivotIndex - 1]
root.right = _buildTree(preorder, pivotIndex - inLeft + preLeft + 1, preRight, inorder, pivotIndex + 1, inRight);//构造右子树
// 前序数组中的[pivotIndex - inLeft + preLeft + 1, preRight] 中序数组中的[pivotIndex + 1, inRight]
//5 返回构造好的二叉树 层序遍历输出 遇到空节点打印null
return root;
}
//02 完成构造
public TreeNode buildTree(int[] preorder, int[] inorder) {
int preLen = preorder.length;
int inLen = inorder.length;
if (preLen != inLen){
throw new RuntimeException("输出有问题!");//大佬还做了异常处理hhh 秀啊
}
return _buildTree(preorder, 0, preLen - 1, inorder, 0, inLen - 1);
//依次输入 前序遍历输入数组 前序遍历左、右边界 中序遍历输入数组 中序遍历左、右边界
}
}
106.从中序与后序遍历序列构造二叉树
根据一棵树的中序遍历与后序遍历构造二叉树。
注意:
你可以假设树中没有重复的元素。
例如,给出
中序遍历 inorder = [9,3,15,20,7]
后序遍历 postorder = [9,15,7,20,3]
返回如下的二叉树:
3
/ \
9 20
/ \
15 7
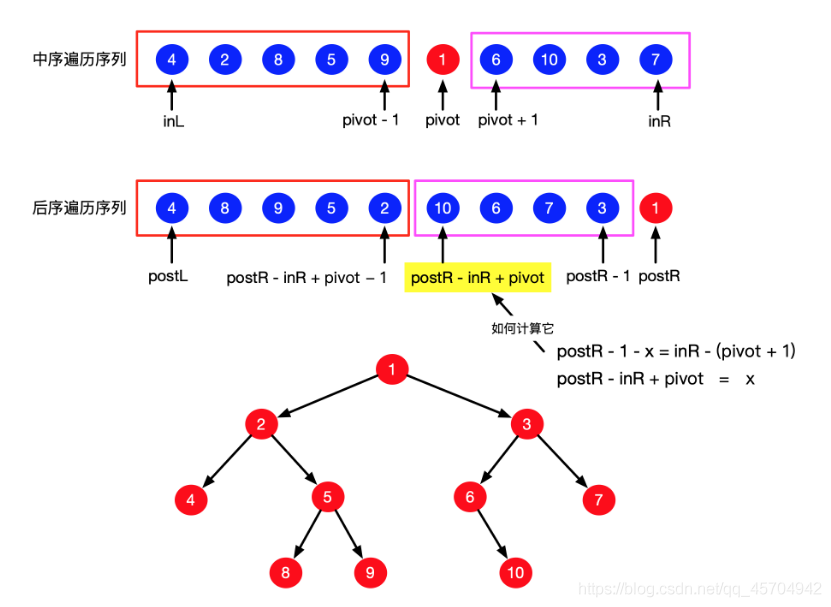
解题思路
依旧是参考威威哥的图解和题解
Java代码
跟上面的解就是换个变量的事儿~ 还是参考的威威哥的题解~
public class Solution {
/**
* 使用中序遍历序列 inorder 的子区间 [inLeft, inRight]
* 与后序遍历序列 postorder 的子区间 [postLeft, postRight] 构建二叉树
*
* @param inorder 中序遍历序列
* @param inLeft 中序遍历序列的左边界
* @param inRight 中序遍历序列的右边界
* @param postorder 后序遍历序列
* @param postLeft 后序遍历序列的左边界
* @param postRight 后序遍历序列的右边界
* @return 二叉树的根结点
*/
private TreeNode buildTree(int[] inorder, int inLeft, int inRight, int[] postorder, int postLeft, int postRight) {
if (inLeft > inRight || postLeft > postRight) {
return null;
}
int pivot = postorder[postRight];
int pivotIndex = inLeft;
// 注意这里如果编写不当,有数组下标越界的风险
while (inorder[pivotIndex] != pivot) {
pivotIndex++;
}
TreeNode root = new TreeNode(pivot);
root.left = buildTree(inorder, inLeft, pivotIndex - 1,
postorder, postLeft, postRight - inRight + pivotIndex - 1);
root.right = buildTree(inorder, pivotIndex + 1, inRight,
postorder, postRight - inRight + pivotIndex, postRight - 1);
return root;
}
// 02 完成构造
public TreeNode buildTree(int[] inorder, int[] postorder) {
int inLen = inorder.length;
int postLen = postorder.length;
// 特判
if (inLen != postLen) {
throw new RuntimeException("输入错误");
}
return buildTree(inorder, 0, inLen - 1, postorder, 0, postLen - 1);
}
}