数学归纳法
我们先来了解一下数学归纳法(这个我高中的时候数学有选修的,可惜老师没讲,但是我自己还是自学了的)
数学归纳法(Mathematical Induction, MI)是一种数学证明方法,通常被用于证明某个给定命题在整个(或者局部)自然数范围内成立。除了自然数以外,广义上的数学归纳法也可以用于证明一般良基结构,例如:集合论中的树。这种广义的数学归纳法应用于数学逻辑和计算机科学领域,称作结构归纳法。——百度百科
我总结其步骤大致为
1.证明初始状态成立;
2.假设某一状态成立;
3.证明2中状态的下一状态也成立;
4.得出结论:对于所有情况都成立——因为我们2中的状态具有普遍性;
假设
如果你在看这个问题,相信你已经知道什么是单色汉诺塔以及单色的解法,而双色汉诺塔如下
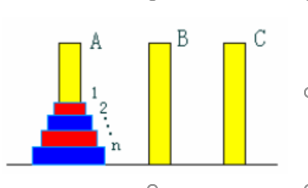
我们不妨将颜色转变为两个状态,假设偶数盘状态为0,奇数盘状态为1。
最容易让人想到的假设是:
1.1个盘肯定满足;
2.假设n-1个盘满足;
证明n个盘满足,证明如下:
n个盘的移动步骤:
1.hanoi(n-1,A,B,C);
2.move(n,A,B);
3.hanoi(n-1,C,A,B);
首先第一步我们已经在2的假设中假设满足,第二步也满足,现在看第三步,将n-1个盘从C借助A移到B,假设B上现在没有第N个盘,显然满足,但是现在有第N个盘,于是我们要证明,在移动过程中,B上的倒数第二的盘(即第N个盘上面的那个)一定与第N个盘奇偶性不同,即与第N-1个盘的奇偶性相同,可以发现,这个证明转化了,而且是回到N-1的规模,即假设2,这就是说,我们这个假设是不太合理的(至于这个假设是能否证明,我认为能,只不过要麻烦一些),我们发现,上述的证明过程提到了N与N-1的奇偶性,不妨在深入一点,即是原始柱,辅助柱与目标柱最下面一个盘的奇偶性(这里我也不知道怎么讲才能更明白,因为我是在一个类似上帝视角,我只能尝试的去解释这个假设的转换如不理解,直接看下面的假设即可,谢谢理解),于是我们更新一下假设:
1.1个盘时显然成立
2.假设n-1个盘满足,且在移动过程中,三个柱子的最下面盘的奇偶性有如下关系:起始柱的奇偶性与辅助柱不同,与目标柱相同(如果n-1个从A柱通过B移到C,那么这个过程中A与C最下面的那个盘的奇偶性相同,而与B不同)——这个显然1个时也满足(0个盘时奇偶性可随便定义);
3.证明n个盘也满足;
证明
不妨设n为偶数,这里1表示奇数盘0为偶数盘,同样的,将n个移动也有三个步骤:
1.hanoi(n-1,A,B,C);
2.move(n,A,B);
3.hanoi(n-1,C,A,B);
起始状态为:
A柱:101010…1(第n-1个盘)0(第n个盘)
B柱:空
C柱:空
1和2显然满足(因为2使我们假设的满足),现在证明3满足,现在的情况如下
A柱:空
B柱:0(第n个盘)
C柱:10101010…1(第n-1个盘)
于是我们将n-1个盘重复n个盘的三个步骤(只不过这里的辅助柱为A,起始柱为C,而n个盘时起始柱为A,辅助柱为B)移动过程中,那么C柱的最低端一直是第n-1个盘,即为1(因为他只需要动一次,具体请看汉诺塔问题),而A柱将一直为0,也就是A:0,B:0,C:1,这是在移动n-1个盘的步骤中必须满足的,但是我们别忘了,这是包含在第n个盘移动的步骤中,于是从第n个盘的角度来说起始柱为A,辅助柱为C,那么必然有A:0,B:0,C:1,可以看到,这个分析无论从第n-1个还是第n个来说,都是相同的,所以显然,第三步也满足,那么显然都满足,假设成立,从而可以看出,双色汉诺塔与单色汉诺塔的移动是没有区别的,因此代码也一样,可以自己去移动验证,下面贴出代码,方便各位验证,当然很多知道单色的应该用不到(请注意以下代码B是最终的目标柱,而不是C)
#include <iostream>
using namespace std;
//递归函数
void hanoi(int n,char a,char b, char c)
{
//判断递归终点
if(n==1)
{
cout<<n<<": "<<a<<" move to "<<b<<endl;
return;
}
//递归主要内容,也有人也说三行代码搞定,大概就是下面的三行吧23333
else
{
hanoi(n-1,a,c,b);
cout<<n<<": "<<a<<" move to "<<b<<endl;
hanoi(n-1,c,b,a);
}
}
int main()
{
int n;
char a='A',b='B',c='C';
cout<<"请输入合适移动的规模,注意规模不能太大"<<endl;
cin>>n;
hanoi(n,a,b,c);
return 0;
}
关于递归函数的事,我们老师说过一句话我觉得很好,递归的函数是你定义的,但是他的操作是上天给的,我的理解就是,因为汉诺塔递归是从后往前的逆过程,人很难去理解计算机怎么操作的(当然你可以一步步手动操作试试),所以我刚学递归时很难理解为啥仅三行就能解决这个问题,因此我们只要处理好边界条件就行,其余的交给电脑吧。学艺不精,若有错误或不严谨的地方烦请指正,或者有更好的理解希望可以分享高见,感谢浏览