CF 811D Color with Occurrences
问：给一个string s，和 n个substring ai，求最少数量的substring覆盖s
转换字符串覆盖问题 -> 区间覆盖问题
区间覆盖：
1. 按左边界升序排
2. 在 左边界 小于/等于/等于+1 当前右边界里，选右边界最远的
当s的长度短，可以使用 数组 做区间覆盖：
ri 代表从 si开始可以覆盖到的最远右边界
规定左右边界协议 和 下标：
左闭右开 or 左闭右闭，0-index or 1-index
‘学习：
1. s.substr(开始， substr长度）
2.s.length() 要 cast 到 int，不然会 RE
3. max_element() 左闭右开
总结：
1. 转换字符串覆盖问题 -> 区间覆盖问题
2. pair区间覆盖 和 数组区间覆盖
3. 规定左右边界 和 下标协议
#include <iostream>
#include <algorithm>
#include <cstring>
#include <map>
#include <vector>
#include <utility>
using namespace std;
/*
1
bababa
2
ba
aba
*/
void solve(){
string s; cin>>s;
int n; cin>>n;
//0 index, 左闭右开
int r[105];
int id[105];
memset(r, 0, sizeof(r));
for(int i=0;i<n;i++){
string sb; cin>>sb;
//应该是 小于等于
for(int j=0;j<=(int)s.length()-(int)sb.length();j++){
//substr(开始， substr的长度)
if(s.substr(j, sb.length())==sb){
//开始 + 长度 超 1
//r[j] in
//左闭右闭 [l, r]
if(j+sb.length() > r[j]){
r[j]=j+sb.length();
id[j]=i;
}
}
}
}
// for(int i=0;i<s.length();i++){
// cout<<r[i]<<" ";
// }
int end=0;
vector<pair<int, int> > ans;
while(end<s.length()) {
//max_element 左闭右开 [r, l)
int next_end=max_element(r, r+end+1)-r;
if(r[next_end] <= end){
cout<<-1<<endl;
return;
}
ans.push_back({id[next_end], next_end});
end=r[next_end];
}
cout<<ans.size()<<endl;
for(int i=0;i<ans.size();i++){
cout<<ans[i].first+1<<" "<<ans[i].second+1<<endl;
}
}
int main(){
int t; cin>>t;
while(t--){
solve();
}
}---------------------------------------------------------------------------------------------------------------------------------
CF1637D Yet Another Minimization Problem
给两个数组a和b，定义一个数组的cost为
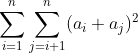
每次操作可以选一个下标 k，交换 ak 和 bk
求两个数组的最小cost和
遇到一个公式，尝试分解到线性:
1. 展开式子
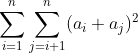2. 分离常数（constant）
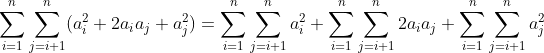
这里把sigma 分配，发现第一项和第三项是常数 （不论怎么换，a和b的都会计算）
3. 转换成线性
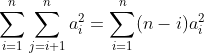
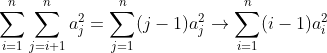
！！！这里注意 j 可以 转成 i
4. 找到不能被分解的式子，要优化（设有多个未知数）
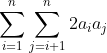
5. 分类合并，简化式子
线性合并一起，平方合并一起
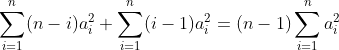
以下为完整公式：
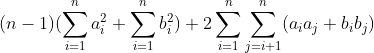
找一个值对cost的贡献
对于aj, 它会与 a1 .. aj-1 的结合 并产生贡献, (a1 * aj) + (a2 * aj) +....(aj-1 *aj)
目前的决策（01, 换或不换）依赖于过去的线性和 与 结果 --> dp
由于ai 和 bi 最大100，n最大100，于是 和 最大 20000
不论怎么换ai和bi，前i个a和b的线性和都是常数
跑01背包-恰好装满j的最小值，
让S[i] 等于a和b的前i个值的和，
让 dp[i][j] 等于 a的前i个值和为j 的最小cost：
if (j >= a[i]) :
if (j >= b[i]) :
总结：
1. 遇到一个公式，尝试分解到线性:
1. 展开式子
2. 分离常数（constant）
3. 分类合并，简化式子
4. 找到不能被分解的式子，要优化（设有多个未知数）
2. 一个下标的贡献？
动态规划？-> 决策
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
int MAX=0x7f7f7f7f;
/*
1
4
3 6 6 6
2 7 4 1
*/
int dp[105][20005];
void solve(){
int n, a[105], b[105];
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<=n;i++) cin>>b[i];
int fConst=0, S[105];
S[0]=0;
for(int i=1;i<=n;i++){
fConst += a[i]*a[i]+b[i]*b[i];
S[i]=S[i-1]+a[i]+b[i];
}
fConst *= (n-1);
//memset(arr, (int)#, size)
memset(dp, MAX, sizeof(dp));
dp[0][0]=0;
for(int i=1;i<=n;i++){
// j 不能！！！从 a[i] 开始
for(int j=0;j<=S[n];j++){
if(j>=a[i]){
dp[i][j]=min(dp[i][j], dp[i-1][j-a[i]]+(j-a[i])*a[i]+(S[i]-j-b[i])*b[i]);
}
if(j>=b[i]){
dp[i][j]=min(dp[i][j], dp[i-1][j-b[i]]+(j-b[i])*b[i]+(S[i]-j-a[i])*a[i]);
}
}
}
int ans=1e9;
for(int j=0;j<=S[n];j++){
ans=min(ans, dp[n][j]);
}
cout<<2*ans + fConst<<endl;
}
int main(){
int t; cin>>t;
while(t--){
solve();
}
}--------------------------------------------------------------------------------------------------------------------------------
CF 811E Add Modulo 10:
给一个数组a，每次操作可以选 i，把a[i] 变成 a[i] + (a[i] mod 10)， 求能否把 所有 ai 变成一样。
通过举例观察到规律 （性质）：
个位会一直在2， 4， 6， 8 循环，之后证明了有于odd+odd=even，even+even=even（除了5），于是每个同阶数的个位都是独特的，比如说 96，十位是9的只有96
一开始的想法：把所有的数的个位变成2，然后打擂台，每次轮回+20 （+4+8+6+2)
正确做法：直接每个数 % 20 就行，会等于 2 or 12，如果 有 2 和 12 则 不可能变一样
打擂台 -> 比较数的性质不同 -> 每个数的性质不同
总结：
ps：已经非常接近答案了，需更耐心的举例 和 细致的观察性质
通过举例观察到规律 （性质）
打擂台 -> 比较数的性质不同 -> 每个数的性质不同
#include <iostream>
#include <algorithm>
using namespace std;
/*
1
3
2 18 22
*/
void solve(){
int n; cin>>n;
int ar[n+5];
for(int i=0;i<n;i++) cin>>ar[i];
for(int i=0;i<n;i++){
while(ar[i]%10!=0 && ar[i]%10!=2) ar[i]+=ar[i]%10;
}
sort(ar, ar+n);
if(ar[n-1]%10==0){
for(int i=0;i<n-1;i++){
if(ar[i]!=ar[n-1]){
cout<<"NO"<<endl;
return;
}
}
cout<<"YES"<<endl;
return;
}
for(int i=1;i<n;i++){
if(ar[i]%20!=ar[i-1]%20){
cout<<"NO"<<endl; return;
}
}
cout<<"YES"<<endl;
}
int main(){
int t; cin>>t;
while(t--){
solve();
}
}