第十届
Fibonacci 数列与黄金分割
时间限制: 1Sec 内存限制: 128MB 提交: 4162 解决: 1172
题目描述
Fibonacci 数列是非常著名的数列:
F[1] = 1,
F[2] = 1,
对于 i > 3,F[i] = F[i − 1] + F[i − 2]
Fibonacci 数列有一个特殊的性质,前一项与后一项的比值,F[i]/F[i + 1], 会趋近于黄金分割。
为了验证这一性质,给定正整数 N,请你计算 F[N]/F[N + 1],并保留 8 位 小数。
输入格式
一个正整数 N。(1 ≤ N ≤ 2000000000)
输出格式
F[N]/F[N + 1]。答案保留 8 位小数。
样例输入
2
样例输出
0.50000000
枚举范围太大,观察发现20项之后,8位小数精度都一样!!!
#include <bits/stdc++.h>
using namespace std;
double fib(int n) {
long long f[n + 1];
f[1] = 1;
f[2] = 1;
for (int i = 3; i <= n; ++i) {
f[i] = f[i - 1] + f[i - 2];
}
return f[n];
}
int main() {
ios::sync_with_stdio(false);
//cin.tie(NULL);
int n;
cin >> n; //cout << fixed << setprecision(8) << fib(n) / fib(n + 1) << endl;
if (n < 20) printf("%.8lf\n",(double)fib(n)/(double)fib(n+1));
else cout << "0.61803399" << endl;
return 0;
}
ios::sync_with_stdio(false);这条语句关掉scanf 和cin 的同步加快效率。但是即使是这样cin 还要慢 5倍左右,而且一旦使用了这条语句,scanf和cin 混用可能就会造成一些奇怪的问题。
修改数组
时间限制: 1Sec 内存限制: 128MB 提交: 5491 解决: 1348
题目描述
给定一个长度为 N 的数组 A = [A1, A2, · · · AN ],数组中有可能有重复出现 的整数。
现在小明要按以下方法将其修改为没有重复整数的数组。小明会依次修改 A2,A3,··· ,AN。
当修改 Ai 时,小明会检查 Ai 是否在 A1 ∼ Ai−1 中出现过。如果出现过,则 小明会给 Ai 加上 1 ;如果新的 Ai 仍在之前出现过,小明会持续给 Ai 加 1 ,直 到 Ai 没有在 A1 ∼ Ai−1 中出现过。
当 AN 也经过上述修改之后,显然 A 数组中就没有重复的整数了。 现在给定初始的 A 数组,请你计算出最终的 A 数组
输入格式
第一行包含一个整数 N。 第二行包含N个整数A1,A2,··· ,AN
对于 80% 的评测用例,1 ≤ N ≤ 10000。
对于所有评测用例,1 ≤ N ≤ 100000,1 ≤ Ai ≤ 1000000。
输出格式
输出N个整数,依次是最终的A1,A2,··· ,AN。
样例输入
5
2 1 1 3 4
样例输出
2 1 3 4 5
并查集思路:
首先我们每输入一个数,都会判断前面是否已经有过,如果有过就会+1,知道前面没有重复的数。
那么像不像并查集的指向呢,如果没有用过就是自己就是一个集合,根节点指向自己
如果已经用过了,只要将其父节点指向比他大1的节点(此时不重复)就可以。
#include<bits/stdc++.h>
using namespace std;
const int N = 1000010;
int p[N];
//查找祖宗节点+路径压缩
int find(int x )
{
if(p[x] != x) p[x] = find(p[x]);
return p[x];
}
int main()
{
int n;
cin>>n;
for(int i = 0; i < N; i++)
p[i] = i;
for(int i = 0; i < n; i++)
{
int x;
scanf("%d",&x);
x = find(x);
printf("%d ",x);
p[x] = x+1;
}
return 0;
}
等差数列
时间限制: 1Sec 内存限制: 128MB 提交: 7792 解决: 1804
题目描述
数学老师给小明出了一道等差数列求和的题目。但是粗心的小明忘记了一 部分的数列,只记得其中 N 个整数。
现在给出这 N 个整数,小明想知道包含这 N 个整数的最短的等差数列有 几项?
输入格式
输入的第一行包含一个整数 N。 第二行包含N个整数A1,A2,···,AN。(注意A1 ∼AN并不一定是按等差数
列中的顺序给出)
(对于所有评测用例,2≤ N ≤100000,0≤ Ai ≤109。)
输出格式
输出一个整数表示答案
样例输入
5
2 6 4 10 20
样例输出
10
乱序先排序,所有相邻两项差的最大公因数, 最大公因数即为 :最大公差d
#include <bits/stdc++.h>
using namespace std;
const int N = 100000;
int a[N];
int gcd(int a,int b)
{
if(b == 0)return a;
return gcd(b,a%b);
}
int main(){
int n;
scanf("%d",&n);
for(int i=0;i<n;i++){
scanf("%d",&a[i]);
}
sort(a,a+n);
//找最小差值的公约数是公差d;
int min=a[0],max=a[n-1];
int d=(a[1]-a[0]);
for(int i=2;i<n;i++){
if((a[i+1]-a[i])<=d){//此处d不能换成a[i]-a[i-1]。
d=gcd(d,a[i]-a[i-1]);//求d与其他差值的公差,赋值
}
}
if(d==0){
printf("%d",n);
}else{
printf("%d",(max-min)/d+1);
}
}
十三届
统计子矩阵
时间限制: 1Sec 内存限制: 256MB 提交: 908 解决: 147
题目描述
给定一个 N × M 的矩阵 A,请你统计有多少个子矩阵 (最小 1 × 1,最大 N × M) 满足子矩阵中所有数的和不超过给定的整数 K?
输入格式
第一行包含三个整数 N, M 和 K.
之后 N 行每行包含 M 个整数,代表矩阵 A.
输出格式
一个整数代表答案。
样例输入
3 4 10
1 2 3 4
5 6 7 8
9 10 11 12
样例输出
19
提示
满足条件的子矩阵一共有 19,包含:
大小为 1 × 1 的有 10 个。
大小为 1 × 2 的有 3 个。
大小为 1 × 3 的有 2 个。
大小为 1 × 4 的有 1 个。
大小为 2 × 1 的有 3 个。
对于 30% 的数据,N, M ≤ 20. 对于 70% 的数据,N, M ≤ 100.
对于 100% 的数据,1 ≤ N, M ≤ 500; 0 ≤ Ai j ≤ 1000; 1 ≤ K ≤ 250000000.
如果直接用 前缀和 + 暴力,复杂度将是O(n4),必须优化
优化的方法是:
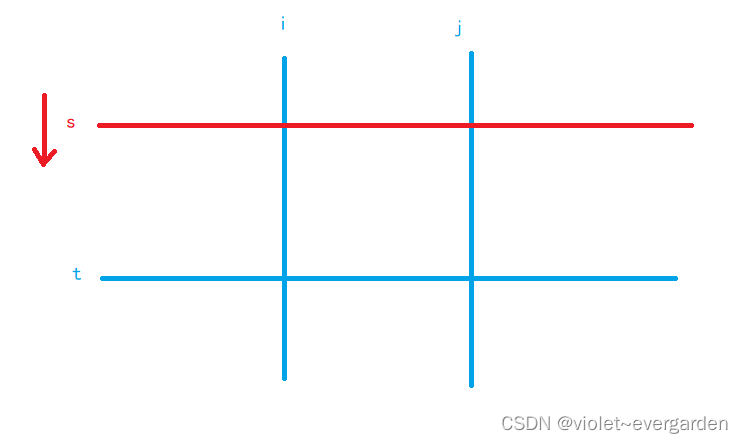
1)枚举子矩阵的 左边界i 和 右边界j,
2)用 快指针t 枚举 子矩阵的下边界,慢指针s 维护 子矩阵的上边界 (s ≤≤ t)
3)如果得到的子矩阵的权值和 大于 k,则慢指针s 前进,而子矩阵和必将单调不增
4)慢指针s 继续前进(如图),直到 子矩阵的和 不大于k,慢指针没必要前进了,因为该子矩阵的所有宽度为 j - i + 1 的子矩阵(总共 t - s + 1 种)一定满足要求,更新该情况对答案的贡献 t - s + 1;反之,如果慢指针s越界(s > t),则不操作,直接进入下层循环
题解
前缀和+暴力O(n4) TLE
复杂度:O(n3)
简记:[l, r枚举: l ~ m] + 双指 (up,down)
ios::sync_with_stdio(false);//记 ios::sysn_with_stdio ,没有特殊格式输出就用cin和cout
初始化直接存二维前缀和 : a[i][j] += a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1];
ll ans = 0;
for(int l=1; l<=m; l++){
for(int r=l; r<=m; r++){ //枚举左右边界 [l,r == l~m]
for(int d = 1, u = 1; u <= n; u ++ ){ // up ~ down 双指针,每次看能down到哪里((l,r)~(up,down) 区间和<k)
while(d <= u && a[u][r] - a[d - 1][r] - a[u][l - 1] + a[d - 1][l - 1] > k) d ++ ;
if(d <= u) ans += u - d + 1;
}
}
}
#include<iostream>
using namespace std;
typedef long long ll;
const int N = 510;
int n, m, k;
int a[N][N];
int main(){
ios::sync_with_stdio(false);//记 ios::sysn_with_stdio ,没有特殊格式输出就用cin和cout
cin >> n >> m >> k;
for(int i=1; i<=n; i++){
for(int j=1; j<=m; j++){
cin >> a[i][j];
a[i][j] += a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1]; //数组直接初始化二维前缀和
}
}
ll ans = 0;
for(int l=1; l<=m; l++){
for(int r=l; r<=m; r++){ //枚举左右边界 [l,r == l~m]
for(int d = 1, u = 1; u <= n; u ++ ){ // up ~ down 双指针,每次看能down到哪里((l,r)~(up,down) 区间和<k)
while(d <= u && a[u][r] - a[d - 1][r] - a[u][l - 1] + a[d - 1][l - 1] > k) d ++ ;
if(d <= u) ans += u - d + 1;
}
}
}
cout << ans << endl; //还可以 : cout << ans '\n' ,但没必要hh
}