虽然这道题标注的是简单,但是对于我一个新手来说还真的挺烧脑的。
我想说:
对于动态规划的知识,我可谓花了大功夫。各种看视频看博客折腾了一整天,不夸张真的是一整天。你以为我懂了,不,这种东西我看下来更本不可能短时间掌握。那在这一整天中我的收获是什么?收获了动态规划的思想及解题步骤。
思想:利用已知的历史记录来完成对未知记录的计算,从而避免重复的计算。
通俗的讲就是我们要将已经计算过的记录进行备份,下次碰见直接拿来用,而不用重新去计算一遍。
那用什么来进行备份?对就是变量,或者是一维数组,或者是二维数组。
解题步骤:
通过走访各大成功人士,总结出动态规划按照如下的几步来完成。
1.定义dp数组所表示的含义
解动态规划题的时候我们都会开辟一个数组,叫dp(Dynamic Programming)数组,可能是一维数组,也有可能是二维数组。我们要明确数组下标所代表的含义及数组元素所代表的意思。
2.确定递推公式
通俗的讲就是确定数组元素间的关系式。这一步很核心,也很难。通常我会从这两个方面来确定:最后一步、子问题。
最后一步:假设前面的若干步已经是全局最优的,那最后一步如何选择也是全局最优。
子问题:将大问题分解成若干的小问题来进行考虑
3.确定初始条件及边界情况
dp数组中一些不能进行分解计算的要直观的给出结果。而边界情况一般就指数组不能越界
4.遍历顺序(计算顺序)
按照怎样的顺序去计算(小->大;大->小)
计算顺序的确定只有一个原则:当要算递推公式等式左边的时候,等式右边用到的状态都已经算过了
光说不练哪还是不行的,下面的这道OJ题我会严格按照如上的解题思想及步骤来完成
原题如下:
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组 是数组中的一个连续部分。
题意:
就是计算一个已知数组的最大连续子序列和。返回这个最大值
按步骤进行:
1.定义dp数组所表示的含义。
我们的问题是求解一个数组中的最大连续子序列和。那我们就定义dp[i]的含义是:nums数组中前 i +1 个数据所组成的数组的最大子序和为dp[i]。
2.确定递推公式。
假设我们要求解 i 个数据的最大子序列和,现在我们已经知道了 i-1 个数据的最大子序列和为dp[i-1]。那么当将最后一个数据加入后,dp[i]的值取决于什么呢?dp[i]的值取决于 dp[i-1] +nums[i] 与nums[i] 中的较大者。所以递推公式为:dp[i]=max(dp[i-1]+nums[i],nums[i]。
3.确定初始条件及边界
哪些情况我们是不能用递推公式分解来计算的。当 i =0时,由于数组下标无负数,所以dp[0]我们要直观的给出。即初始化:dp[0]=nums[0],边界情况为数组不能越界,也就是dp数组的大小为给定数组的大小。
3.计算顺序
根据递推公式等式左边的要等与等式右边的,而i > i -1,则说明要从小到大进行遍历。
示意图如下: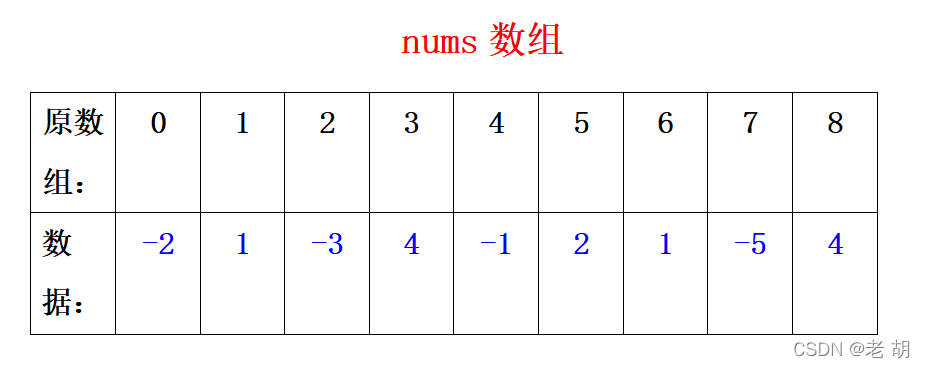
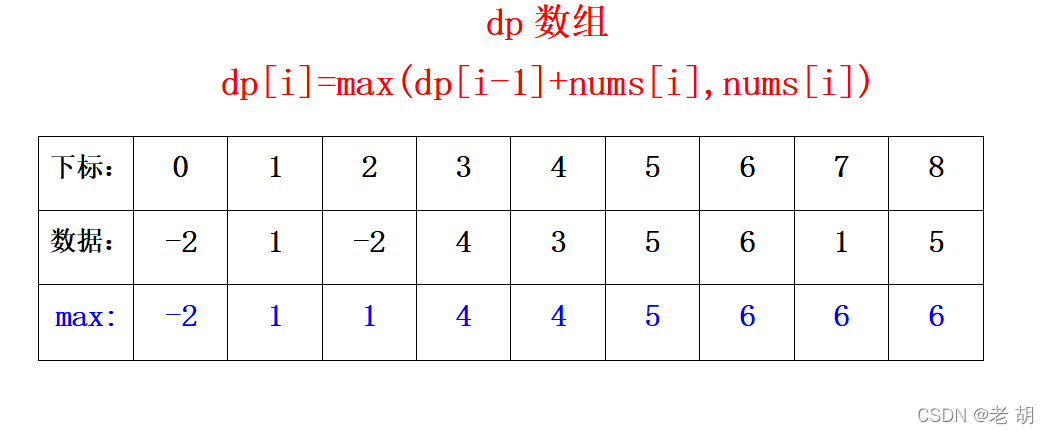
代码实现:
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int numsSize=nums.size();//数组大小,为nums数组的大小
vector<int>dp(numsSize);//开辟dp数组
dp[0]=nums[0];//不能分解的情况
int Max=dp[0];//用于标记最大子序列和
for(int i=1;i<numsSize;i++)
{
dp[i]=max(dp[i-1]+nums[i],nums[i]);
Max=max(dp[i],Max);
}
return Max;//返回最大子序列和
}
};
按照上面的思路步骤确实是可行的,当然以后的时间我也会用实践来证明。
我是老胡,感谢阅读!!❤️ ❤️