1. 问题描述:
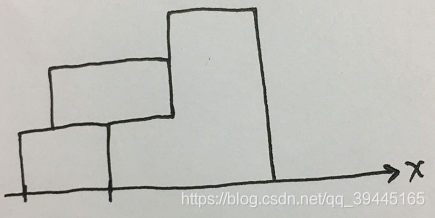
在无限长的数轴(即 x 轴)上,我们根据给定的顺序放置对应的正方形方块。第 i 个掉落的方块(positions[i] = (left, side_length))是正方形,其中 left 表示该方块最左边的点位置(positions[i][0]),side_length 表示该方块的边长(positions[i][1])。每个方块的底部边缘平行于数轴(即 x 轴),并且从一个比目前所有的落地方块更高的高度掉落而下。在上一个方块结束掉落,并保持静止后,才开始掉落新方块。方块的底边具有非常大的粘性,并将保持固定在它们所接触的任何长度表面上(无论是数轴还是其他方块)。邻接掉落的边不会过早地粘合在一起,因为只有底边才具有粘性。返回一个堆叠高度列表 ans 。每一个堆叠高度 ans[i] 表示在通过 positions[0], positions[1], ..., positions[i] 表示的方块掉落结束后,目前所有已经落稳的方块堆叠的最高高度。
示例 1:
输入: [[1, 2], [2, 3], [6, 1]]
输出: [2, 5, 5]
解释:
第一个方块 positions[0] = [1, 2] 掉落:
_aa
_aa
-------
方块最大高度为 2 。
第二个方块 positions[1] = [2, 3] 掉落:
__aaa
__aaa
__aaa
_aa__
_aa__
--------------
方块最大高度为5。
大的方块保持在较小的方块的顶部,不论它的重心在哪里,因为方块的底部边缘有非常大的粘性。
第三个方块 positions[1] = [6, 1] 掉落:
__aaa
__aaa
__aaa
_aa
_aa___a
--------------
方块最大高度为5。
因此,我们返回结果[2, 5, 5]。
示例 2:
输入: [[100, 100], [200, 100]]
输出: [100, 100]
解释: 相邻的方块不会过早地卡住,只有它们的底部边缘才能粘在表面上。
注意:
1 <= positions.length <= 1000.
1 <= positions[i][0] <= 10 ^ 8.
1 <= positions[i][1] <= 10 ^ 6.
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/falling-squares
2. 思路分析:
分析题目可以知道我们可以将每一个落在数轴上的方块看成是一个区间,我们要求解的是在当前区间每落一个方块在数轴上之后所有区间的最大高度,也即每一次加入一个区间的时候当前所有区间的最大高度,所以当我们每一次加入一个区间之后都要维护当前区间的高度为上一次区间高度的最大值加上当前方块对应的高度,并且我们需要查询区间高度的最大值,我们应该使用什么样的数据结构来维护这些信息呢?因为涉及到修改整个区间的最大高度,并且需要查询区间高度的最大值,所以我们可以使用线段树来维护(遇到区间修改的问题需要想到线段树),区间修改的问题需要使用带有懒标记的线段树来解决,并且带有懒标记的线段树比不带有懒标记的线段树要复杂一些。
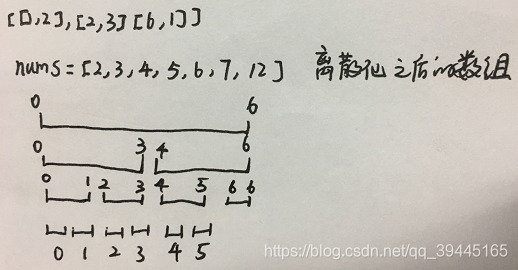
因为题目中每个点的数据范围比较大,而且对应在x轴上的区间个数比较少,所以我们需要将数轴上的端点进行离散化,离散化其实是将分散比较远的点将其映射到一段连续的区间,这样可以避免开很大的数组造成空间太大溢出的问题(离散化 + 线段树其实关心的是点的数目而不是数值),因为线段树在查询与更新区间的时候需要计算当前区间[a, b]的中点我们可以将所有的位置先放大两倍,这样可以避免寻找中点的时候由于除法造成的精度问题,并且离散化之后查找区间[a + 1,b - 1]可能是不存在的,所以在离散化的时候需要将[a, b]之间的中点加进来这样可以确定[a, b]是一定存在点的,因为是点放大了两倍所以我们在离散化的时候加入a + b这个点即可。下面使用java语言的线段树版本来解决这个问题,带有懒标记的线段树比不带有懒标记的线段树多一个pushdown下传的方法,下面是具体的五个方法:
- void pushup(int u),将当前根节点表示的两个子区间的区间高度最大值更新到当前根节点表示的区间高度最大值,当前的区间是以mid作为分隔点划分为两个子区间的,[l,mid]为左边的区间,[mid + 1,r]为右边的区间,所以子区间的最大值就是当前区间高度的最大值
- void build(int u, int l, int r),创建[l,r]的区间的线段树,创建的过程其实是一个递归的过程,以mid作为分隔点,[l,mid]为左边的区间,[mid + 1,r]为右边的区间,创建的时候更新区间的左右端点l,r
- void pushdown(int u),将当前根节点的懒标记更新到左右两个子区间,并且当当前根节点的懒标记只会下传一次,因为下传之后将当前根节点的懒标记置为0
- void update(int u, int l, int r, int c),将当前区间[l,r]的值全部更新为c,更新的时候更新懒标记即可,懒标记的一个作用是避免所有的区间的所有节点都更新的问题造成耗时太大的问题。在更新整个区间的时候需要调用pushup和pushdown方法
- int query(int u, int l, int r),查询区间[l, r]的最大高度,这个方法与不带懒标记的查询方法是类似的
这五个方法主要是理解递归创建、修改、查询的过程,结合区间对应的二叉树的图会更好理解一点。

3. 代码如下:
java代码:
import java.util.*;
public class Solution {
// 线段树的根节点编号从1开始
static Tree tr[];
public static List<Integer> fallingSquares(int[][] positions) {
Map<Integer, Integer> map = new HashMap<Integer, Integer>();
for (int i = 0; i < positions.length; ++i){
int a, b;
a = positions[i][0];
// b表示区间的右端点
b = a + positions[i][1];
// 离散化, 将坐标扩大两倍, 加入a + b是为了后面保证查询区间[a+1,b-1]是存在的
map.put(2 * a, map.getOrDefault(a, 0) + 1);
map.put(2 * b, map.getOrDefault(b, 0) + 1);
// 这个点千万要加,不加答案是不正确的, 例如不加例子[[1,5],[2,2],[7,5]]答案就是错误的, 因为离散化之后可能导致[a+1,b-1]区间是不存在的这样查询的结果为0就不正确了
map.put(a + b, map.getOrDefault(b, 0) + 1);
}
// 因为离散化之后可能加入了重复的数字所以先使用哈希表计数, 哈希表中的键表示的就是不重复的数字
List<Integer> nums = new ArrayList<Integer>();
for (Map.Entry<Integer, Integer> m: map.entrySet()){
nums.add(m.getKey());
}
// 离散化之后需要将这些点进行排序
Collections.sort(nums);
int n = nums.size();
tr = new Tree[4 * n];
// 初始化每一个线段树节点
for (int i = 1; i < 4 * n; ++i){
tr[i] = new Tree();
}
// 创建线段树, 维护所有区间根节点表示的左右端点
build(1, 0, nums.size() - 1);
List<Integer> res = new ArrayList<Integer>();
int a, b;
for (int []p: positions){
a = p[0];
// b为右端点
b = a + p[1];
a = get(nums, a * 2);
b = get(nums, b * 2);
// 查询区间[a + 1, b - 1]的高度
int h = query(1, a + 1, b - 1);
// 将当前区间[a,b]的高度全更新为新的高度
update(1, a, b, h + p[1]);
// 第一个根节点的值就是所有区间的最大高度
res.add(tr[1].v);
}
return res;
}
// 二分查找出当前的x在nums中的下标
public static int get(List<Integer> nums, int x){
int l = 0, r = nums.size() - 1;
while (l < r){
int mid = l + r >> 1;
// 答案一定是在左边
if (nums.get(mid) >= x) r = mid;
else l = mid + 1;
}
return r;
}
// 将当前根节点区间的左右两个子区间的最大值更新到当前的根节点表示的最大值上
public static void pushup(int u){
tr[u].v = Math.max(tr[u << 1].v, tr[u << 1 | 1].v);
}
// 递归创建线段树, 初始化当前根节点的区间左右端点范围
public static void build(int u, int l, int r){
tr[u].l = l;
tr[u].r = r;
if (l == r) return;
int mid = l + r >> 1;
build(u << 1, l, mid);
build(u << 1 | 1, mid + 1, r);
// 因为一开始的时候区间和为0所以不用pushup操作
}
// 将线段树的懒标记下传到子区间
public static void pushdown(int u){
int c = tr[u].c;
Tree l = tr[u << 1], r = tr[u << 1 | 1];
// 只有当懒标记存在的时候才将懒标记下传到子区间
if (c > 0){
// 因为后面在更新的时候是将某个区间数更新为另外一个数字(区间高度的最大值)所以将对应的区间最大值和懒标记都更新为c, c其实是区间高度的最大值, 调用这个方法的时候将这个值也作为懒标记的值
tr[u].c = 0; // 将当前根节点的懒标记置为0这样懒标记只会传递一次
l.c = c;
r.c = c;
l.v = c;
r.v = c;
}
}
// 带有懒标记的线段树的核心方法
public static void update(int u, int l, int r, int c){
if (tr[u].l >= l && tr[u].r <= r){
// 当前根节点的区间在[l,r]范围之内更新懒标记和区间高度最大值返回即可
tr[u].c = tr[u].v = c;
return;
}
// 将懒标记下传并且懒标记下传到子区间的时候只会下传一次, 因为在下传的时候会将当前根节点的懒标记置为0这样这样下次就不会往下传了
pushdown(u);
int mid = tr[u].l + tr[u].r >> 1;
// 因为左边的区间位于[l,r]之内所以需要更新一下左边的区间
if (l <= mid){
update(u << 1, l, r, c);
}
// 因为右边的区间位于[l,r]之内所以需要更新一下右边的区间
if (r > mid){
update(u << 1 | 1, l, r, c);
}
// 将当前根节点对应的区间的两个子区间高度的最大值传递到当前根节点表示的区间
pushup(u);
}
// 查询区间[l, r]的最大高度
public static int query(int u, int l, int r){
// 当前根节点表示的区间在[l,r]范围之内直接返回v即可
if (tr[u].l >= l && tr[u].r <= r){
return tr[u].v;
}
// 下传懒标记这样计算的答案才正确的
pushdown(u);
int mid = tr[u].l + tr[u].r >> 1;
int res = 0;
// 左边的区间满足要求
if (mid >= l){
res = query(u << 1, l, r);
}
// 右边的区间满足要求
if (mid < r){
res = Math.max(res, query(u << 1 | 1, l, r));
}
return res;
}
public static class Tree{
// v为当前区间[l,r]的最大高度, c为懒标记
int l, r, v, c;
}
}c++代码:
const int N = 3010;
struct Node {
int l, r, v, c;
}tr[N << 2];
class Solution {
public:
vector<int> xs;
int get(int x) {
return lower_bound(xs.begin(), xs.end(), x) - xs.begin();
}
void pushup(int u) {
tr[u].v = max(tr[u << 1].v, tr[u << 1 | 1].v);
}
void pushdown(int u) {
int c = tr[u].c;
if (c) {
auto &l = tr[u << 1], &r = tr[u << 1 | 1];
tr[u].c = 0;
l.v = r.v = c;
l.c = r.c = c;
}
}
void build(int u, int l, int r) {
tr[u] = {l, r};
if (l == r) return;
int mid = l + r >> 1;
build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
}
void update(int u, int l, int r, int c) {
if (tr[u].l >= l && tr[u].r <= r) {
tr[u].c = tr[u].v = c;
return;
}
pushdown(u);
int mid = tr[u].l + tr[u].r >> 1;
if (l <= mid) update(u << 1, l, r, c);
if (r > mid) update(u << 1 | 1, l, r, c);
pushup(u);
}
int query(int u, int l, int r) {
if (tr[u].l >= l && tr[u].r <= r) return tr[u].v;
pushdown(u);
int mid = tr[u].l + tr[u].r >> 1;
int res = 0;
if (l <= mid) res = query(u << 1, l, r);
if (r > mid) res = max(res, query(u << 1 | 1, l, r));
return res;
}
vector<int> fallingSquares(vector<vector<int>>& pos) {
for (auto& p: pos) {
int a = p[0], b = a + p[1];
xs.push_back(a * 2), xs.push_back(b * 2), xs.push_back(a + b);
}
sort(xs.begin(), xs.end());
xs.erase(unique(xs.begin(), xs.end()), xs.end());
build(1, 0, xs.size() - 1);
vector<int> res;
for (auto& p: pos) {
int a = p[0], b = a + p[1];
a = get(a * 2), b = get(b * 2);
int h = query(1, a + 1, b - 1);
update(1, a, b, h + p[1]);
res.push_back(tr[1].v);
}
return res;
}
};