Aggregating CVSS Base Scores for Semantics-Rich Network Security Metrics
一、摘要
在计算攻击图评估指标的时候,通常会用到CVSS得分,但这往往会导致漏洞信息的缺失。我们往往只关心这个漏洞的得分是多少,然后直接使用这个得分计算,而忽视了实际的网络拓扑环境,这是不合理的,本文提出了一种评估漏洞之间依赖关系的方法。
二、相关技术介绍
(一)CVSS2.0计算
CVSS2.0得分包含六个指标,分别是Access Vector、Access Complexity、Authentication、Confidentiality Impact、Integrity Impact、Availability Impact。下面的表格中记录了每一个指标的取值情况。
Access Vector(AV)攻击途径
| 名称 | 描述 | 得分 |
|---|---|---|
| Local | 通过本地物理接触攻击或本地shell攻击 | 0.395 |
| Adjacent Network | 相邻网络攻击(子网, 蓝牙等) | 0.646 |
| Network | 远程网络攻击 | 1.0 |
Access Complexity(AC)攻击复杂度
| 名称 | 描述 | 得分 |
|---|---|---|
| High (H) | 复杂度高, 需要获取系统权限等 | 0.35 |
| Medium (M) | 复杂度中, 需要获取系统部分权限等 | 0.61 |
| Low (L) | 复杂度低 | 0.71 |
Authentication(Au)认证
| 名称 | 描述 | 得分 |
|---|---|---|
| Multiple (M) | 需要多次认证 | 0.45 |
| Single (S) | 需要一次认证 | 0.56 |
| None (N) | 不需要认证 | 0.704 |
Confidentiality Impact(C)机密性
| 名称 | 描述 | 得分 |
|---|---|---|
| None | 不影响 | 0.0 |
| Partial | 部分影响 | 0.275 |
| Complete | 完全影响 | 0.660 |
Integrity Impact(I)完整性
| 名称 | 描述 | 得分 |
|---|---|---|
| None | 不影响 | 0.0 |
| Partial | 部分影响 | 0.275 |
| Complete | 完全影响 | 0.660 |
Availability Impact(A)可用性
| 名称 | 描述 | 得分 |
|---|---|---|
| None | 不影响 | 0.0 |
| Partial | 部分影响 | 0.275 |
| Complete | 完全影响 | 0.660 |
计算公式如下:
(二)现有评估指标的不足
传统的CVSS得分是不能体现出漏洞之间的依赖关系。给出如下实例网络: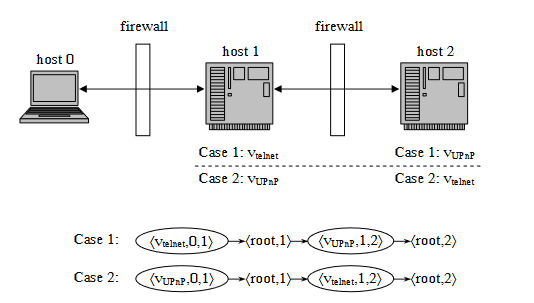
分为两种情况,第一种情况下host1上执行telnet服务,host2执行Upnp服务;第二种情况下两台主机host1和host2上的服务对换。
host0表示攻击者,那么我们可以得到两条攻击链,对于Vtelnet和VUpnp的相关参数如下表: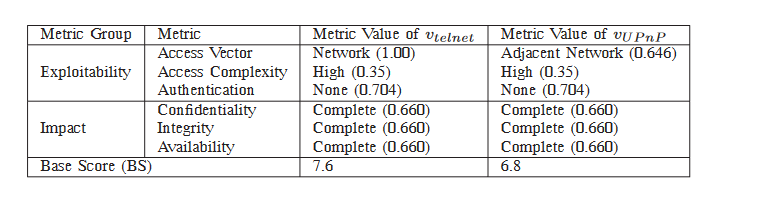
利用前面(一)提到的公式可以很容易的计算两个漏洞的CVSS得分。我们可以发现如果对这一网络采用最大值和平均值指标,case1和case2是无法被区分开的,最大值都是7.6,平均值都是(7.6+6.8)/ 2 = 7.2。为了解决这种情况,我们可以使用贝叶斯网络模型。下面对贝叶斯模型简要介绍:
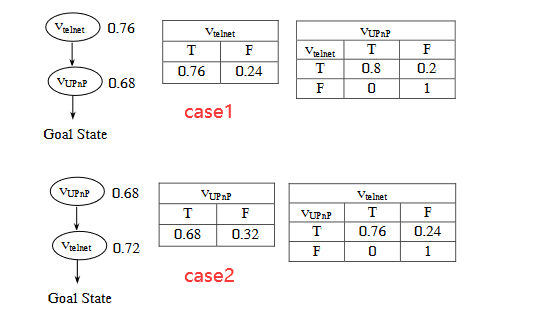
对于case1,可以计算P(VUPnP=T)的概率,计算公式如下: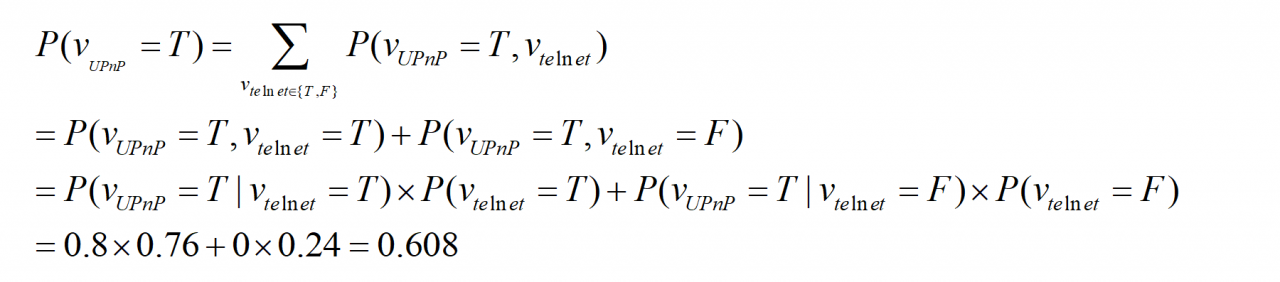
对于case2,可以计算P(Vtelnet=T)的概率,计算公式如下: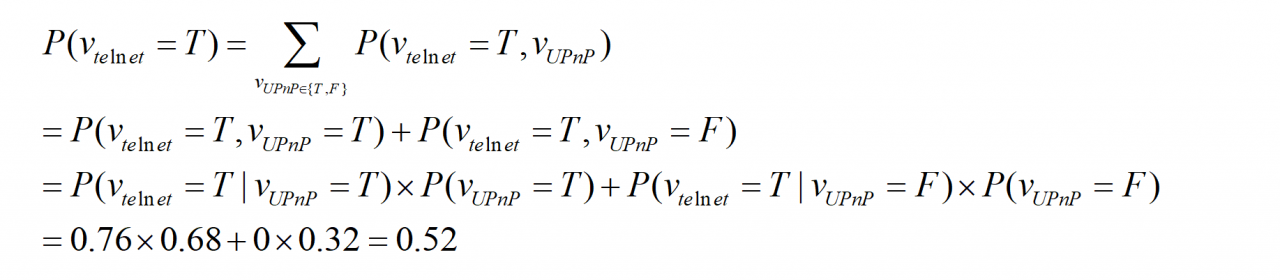
小结:通过贝叶斯模型能够实现体现出case1和case2的差异,能在一定程度上体现出依赖关系,但是概率表中的0.8是我们人为设计的,并不是一个精确计算得到的值。
综合考虑上面方法的优缺点,我们提出了一个评估值来修正其他漏洞带来的影响值。
对于这个网络,我们需要注意的一点是对于case1,攻击者已经利用telnet漏洞获得了host1的root权限,这时候再访问host2,Access Vector值不应该去Adjacent Network,应该修正为Network。那么重新计算得分之后,VUPnP的得分就从6.8变为修正后的7.6。我们重新计算得分,把之前人为定义的0.8用新得到的值0.76替换,可以得到P(VUPnP=T)修正后的值为0.58。
case2计算的得分不变,还是0.52,通过使用修正后的CVSS得分可以表示出漏洞之间的依赖关系。
三、结合例子说明
(一)相关定义
定义一:如果一个结点它的祖先结点和它之间没有依赖关系,那么我们定义有效基础指标值(ebm)就等于基础指标(bm),如果有祖先结点和这个结点之间存在依赖关系,取最大的调整值。(依赖关系可能不唯一,调整值可能有很多个,我们要取最大的一个)。
定义二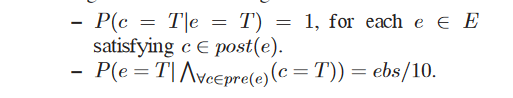
定义了两个公式,第一个公式就表示后置条件在条件满足的时候发生的概率是1;如果c是e的前置条件,那么e为真的概率应该是等于e所有的前置条件发生概率之和。下面结合拓扑实例分析: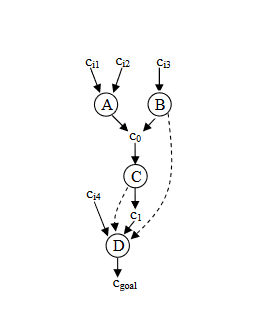
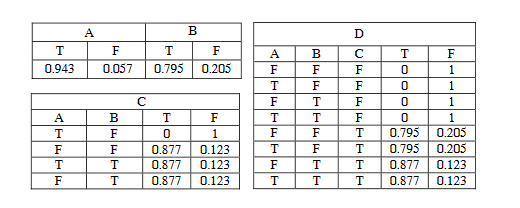
结合拓扑图和贝叶斯概率表,可以得到: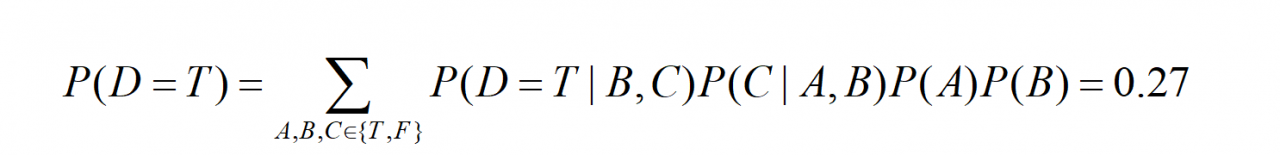
(二)举例
我们需要考虑到攻击者需要花费的代价和攻击者水平。
攻击者需要花费的代价包括时间代价和利用代价。比如一个不需要身份验证的漏洞一定是要比需要身份验证的漏洞节约时间和精力的。攻击水平是对于AccessComplexity中取High的话就会比取low的攻击能力要求更高。我们以下图为例,虚线表示两台主机之间存在依赖关系。右表给出了CVSS对于指标的取值,es,ss是我们算的一个评估值。结合我们前面提到的调整值,当出现依赖关系的时候需要调整CVSS指标的取值,比如A和C之间存在依赖关系,结合右表可以看到VC的AV值是Local,但是AC之间存在依赖关系,我们需要把C的AV值调整成Network。同理,EF之间也存在依赖关系,我们把F的Au值从Single调整成None。
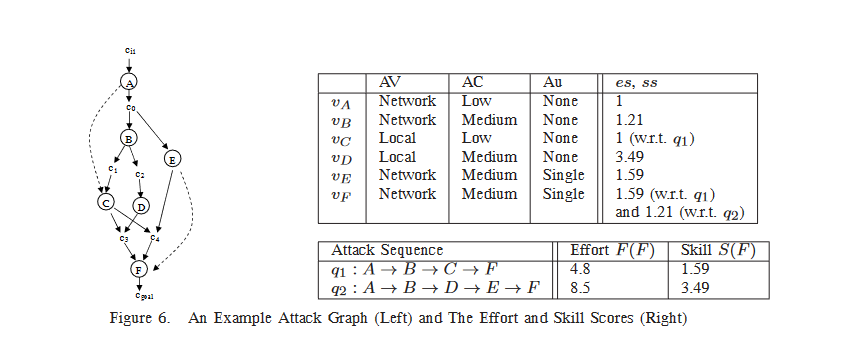
这里给出计算es,ss的公式如下: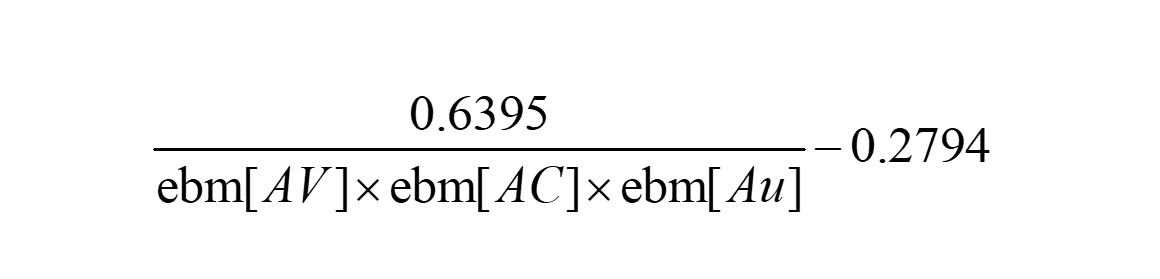
对于这张图可以得到两个攻击序列q1,q2。需要注意一点,攻击序列并不是攻击路径,它指标是对于条件的利用顺序。
对于VA的es,ss计算如下:(BDE计算过程类似)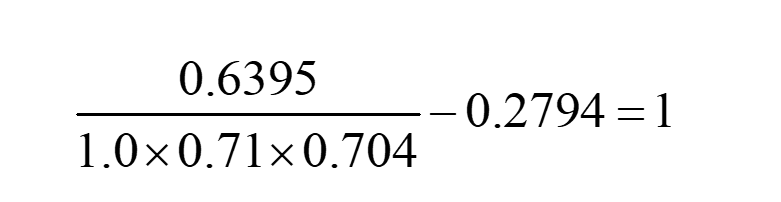
对于VC的es,ss计算需要注意,AC之间存在依赖关系,ebm应该用调整值。我们需要把C的AV值修改为Network再计算,计算公式如下: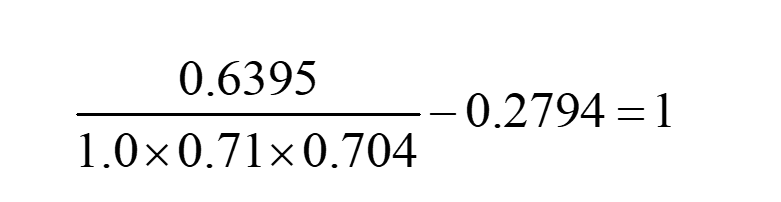
最后来计算VF的es,ss值。需要注意的一点是两个攻击序列中都有F,而且q1中的F是不受到依赖关系影响的,他的评估值ebm就是本身的分数。然而q2中的F是受到依赖关系影响的,EF的依赖关系会使得F的Au值变为None。计算公式如下: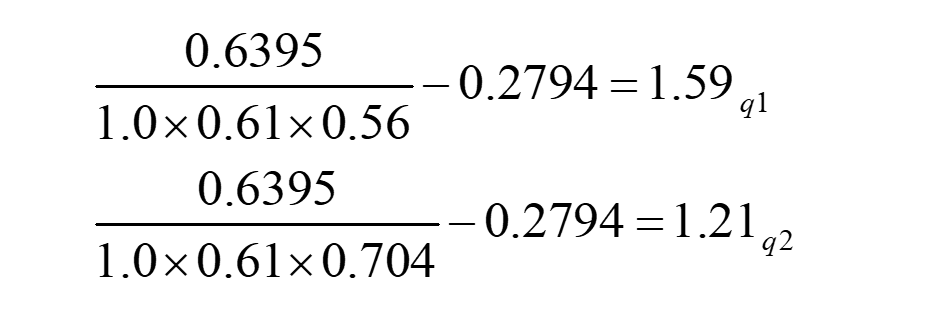
得到了每个点的es,ss值之后,可以计算两个指标:Effort和Skill。分别表示攻击者需要花费的代价和攻击能力。Effort的计算就是把这条攻击序列上所有点的es,ss值加起来。Skill的计算是找到这条攻击序列上攻击者需要的最高能力。