面向金融的R语言——Lecture7

2018年11月15日 软微 金融信息服务 刘旭德

文章目录

• 面向金融的R语言——Lecture7
• 黄金分割搜索方法
• • example

黄金分割搜索方法

前提是什么？
最值唯一，还有么？

黄金分割的搜索方法是一种迭代的搜索方法，对 [a , b]的区间不断缩小，缩小的倍数采用黄金分割比例，目的是为了减少计算量，选用其它任意比例也可。当$b-a$ 足够小时，最小值就在区间 a 和 b 之间
具体如思路如下：
定义一个 gold_method 的方法，假设最小值唯一，在区间 [a, b] 内部，有 x1 ，x2，
如果 f(x1) < f(x2),那么最小值一定在 x2 的左边。$[a^1,b^2]=[a,x2]$

为什么呢？如果图形不是一个单凸的呢？

如果 f(x1) > f(x2) ,那么最小值一定在 x1 的右边。 $[a^1,b^2]=[x1,b]$
用这种方法直到达到容忍标准。
在 a, b 之间选择点用黄金分割比例， $ratio=1/(\sqrt{(}5)+1)$
$$f=\left|x-3.5\right|+(x-2{)}^2$$

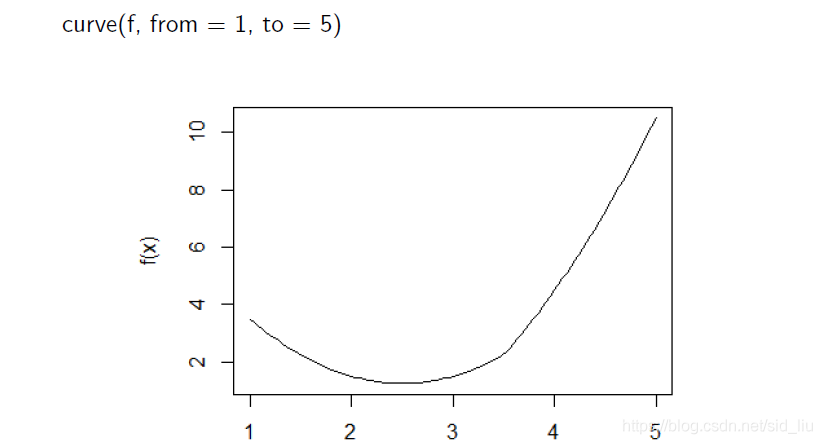
gold_function <- function(f, a, b, tol = 0.0000001){
  ratio <- 2 / (sqrt(5) + 1)
  x1 <- b - ratio * (b - a)
  x2 <- a + ratio * (b - a)
  f1 <- f(x1)
  f2 <- f(x2)
  while(abs(b - a) > tol){
    if (f2 > f1){
      b <- x2
      # 由黄金比例所决定的，可以少算一个值
      # 用x2 <- a + ratio * (b - a)也可以
      x2 <- x1
      f2 <- f1
      x1 <- b - ratio * (b - a)
      f1 <- f(x1)
    }else{
      a <- x1
      x1 <- x2
      f1 <- f2
      x2 <- a + ratio * (b - a)
      f2 <- f(x2)
    }
  }
  return((a + b) / 2)
}

# 执行函数gold_function()
f <-function(x = 0) abs(x - 3.5) + (x - 2) ^ 2
curve(f, 2, 5)
gold_function(f, 2, 5)

out:

> # 执行函数gold_function()
> f <-function(x = 0) abs(x - 3.5) + (x - 2) ^ 2
> gold_function(f, 2, 5)
[1] 2.5

example

Q1:

A1: