图的深度优先遍历

深度优先搜素（Depth First Search ，DFS）是最常见的图的搜索之一，深度优先搜索沿着一条路径一直搜索下去，在无法搜索时，返回到刚刚访问的节点。
深度优先的特征是：后被访问的节点，其领接点先被访问。
根据深度优先遍历的特征：后来者先服务，和数据结构栈的特征一样。所以可以借助栈来实现。使用递归也可以实现深度优先搜素，但递归本身也是使用栈实现的。
1、算法步骤
（1）初始化图中所有节点均未访问。
（2）从图中某个节点v出发，访问v并标记为已访问。
（3）依次检查v的所有邻接点w，如果w未被访问，则从w出发进行深度优先遍历（递归调用，重复2~3步骤）
如图：
一个无向图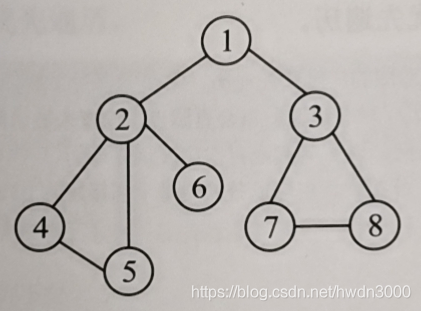

初始化所有节点均未被访问，visited[i]=false,i=1,2,…,8。
从节点1出发，标记其被访问，visited[1]=true。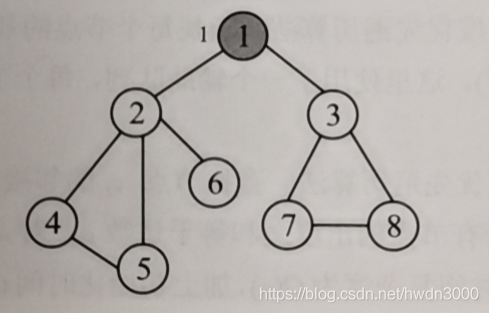

从节点2出发访问领接点2，然后从2出发访问4，从4出发访问5，从5出发没有未被访问的邻接点。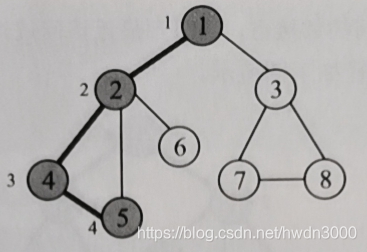

回到刚刚访问过的领接点4,4也没有未被访问的邻接点，再回到2，从2出发访问下一个未被访问的6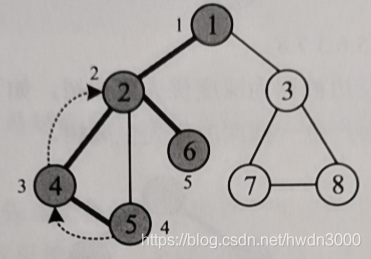

6再没有被访问的邻节点回到2，2再没有访问的邻接点，回到1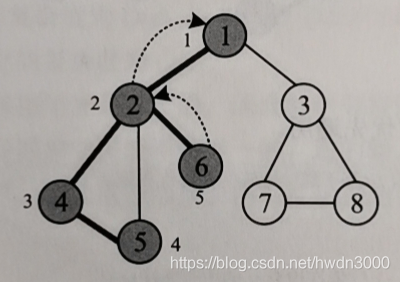

从1访问下一个未被访问的3，从3访问7，从7访问8,8没有可以访问的邻接点。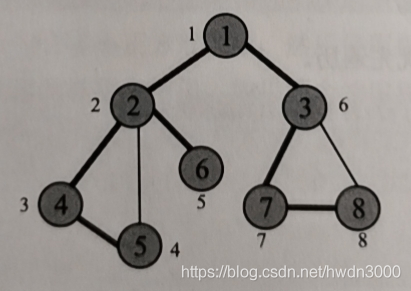

8退回到7,7退回到3,3退回到1，节点1也没有被访问的邻接点，遍历结束。
深度优先遍历的序列为1 2 4 5 6 3 7 8

邻接矩阵存图代码：

#include<iostream>
using namespace std;
const int MaxVnum=100;     //顶点数最大值
bool visited[MaxVnum];  //访问标志数组，其初值为"false"
typedef char VexType;  //顶点的数据类型，根据需要定义
typedef int EdgeType;  //边上权值的数据类型，若不带权值的图，则为0或1
typedef struct{
	VexType Vex[MaxVnum];
	EdgeType Edge[MaxVnum][MaxVnum];
	int vexnum,edgenum; //顶点数，边数
}AMGraph;

int locatevex(AMGraph G,VexType x){
    for(int i=0;i<G.vexnum;i++)//查找顶点信息的下标
		if(x==G.Vex[i])
			return i;
    return -1;//没找到
}

void CreateAMGraph(AMGraph &G){//创建无向图的邻接矩阵
    int i,j;
    VexType u,v;
    cout<<"请输入顶点数："<<endl;
    cin>>G.vexnum;
    cout<<"请输入边数:"<<endl;
    cin>>G.edgenum;
    cout<<"请输入顶点信息:"<<endl;
    for(int i=0;i<G.vexnum;i++)//输入顶点信息，存入顶点信息数组
        cin>>G.Vex[i];
    for(int i=0;i<G.vexnum;i++)//初始化邻接矩阵所有值为0，如果是网，则初始化邻接矩阵为无穷大
		for(int j=0;j<G.vexnum;j++)
			G.Edge[i][j]=0;
    cout<<"请输入每条边依附的两个顶点："<<endl;
    while(G.edgenum--){
		cin>>u>>v;
		i=locatevex(G,u);//查找顶点u的存储下标
		j=locatevex(G,v);//查找顶点v的存储下标
		if(i!=-1&&j!=-1)
			G.Edge[i][j]=G.Edge[j][i]=1; //若有向图G.Edge[i][j]=1
		else{
			cout<<"输入顶点信息错！请重新输入！"<<endl;
			G.edgenum++;//本次输入不算
		}
    }
}

void print(AMGraph G){//输出邻接矩阵
    cout<<"图的邻接矩阵为："<<endl;
    for(int i=0;i<G.vexnum;i++){
        for(int j=0;j<G.vexnum;j++)
        	cout<<G.Edge[i][j]<<"\t";
        cout<<endl;
    }
}

void DFS_AM(AMGraph G,int v){//基于邻接矩阵的深度优先遍历
    int w;
    cout<<G.Vex[v]<<"\t";
    visited[v]=true;
    for(w=0;w<G.vexnum;w++)//依次检查v的所有邻接点
		if(G.Edge[v][w]&&!visited[w])//v、w邻接而且w未被访问
			DFS_AM(G,w);//从w顶点开始递归深度优先遍历
}

int main(){
    int v;
    VexType c;
    AMGraph G;
    CreateAMGraph(G);//创建无向图的邻接矩阵 
    print(G);
    cout<<"请输入遍历连通图的起始点：";
	cin>>c;
	v=locatevex(G,c);//查找顶点u的存储下标
    if(v!=-1){
        cout<<"深度优先搜索遍历连通图结果："<<endl;
        DFS_AM(G,v);
    }
    else
        cout<<"输入顶点信息错！请重新输入！"<<endl;
    return 0;
}
/*测试数据 
8 9
1 2 3 4 5 6 7 8
1 3
1 2
2 6
2 5
2 4
3 8
3 7
4 5
7 8
1
*/ 

领接表存图代码

#include<iostream>
using namespace std;
const int MaxVnum=100;  //顶点数最大值
bool visited[MaxVnum];  //访问标志数组，其初值为"false"
typedef char VexType;   //顶点的数据类型为字符型
typedef struct AdjNode{ //定义邻接点类型
	int v; //邻接点下标
	struct AdjNode *next; //指向下一个邻接点
}AdjNode;

typedef struct VexNode{ //定义顶点类型
   VexType data; // VexType为顶点的数据类型，根据需要定义
   AdjNode *first; //指向第一个邻接点
}VexNode;

typedef struct{//定义邻接表类型
    VexNode  Vex[MaxVnum];
    int vexnum,edgenum; //顶点数，边数
}ALGraph;

int locatevex(ALGraph G,VexType x){
    for(int i=0;i<G.vexnum;i++)//查找顶点信息的下标
		if(x==G.Vex[i].data)
        	return i;
    return -1;//没找到
}

void insertedge(ALGraph &G,int i,int j){//插入一条边
    AdjNode *s;
    s=new AdjNode;
    s->v=j;
    s->next=G.Vex[i].first;
    G.Vex[i].first=s;
}

void printg(ALGraph G){//输出邻接表
	cout<<"----------邻接表如下：----------"<<endl;
	for(int i=0;i<G.vexnum;i++){
		AdjNode *t=G.Vex[i].first;
		cout<<G.Vex[i].data<<"：  ";
		while(t!=NULL){
		   cout<<"["<<t->v<<"]  ";
		   t=t->next;
		}
		cout<<endl;
	}
}

void CreateALGraph(ALGraph &G){//创建无向图邻接表
    int i,j;
    VexType u,v;
    cout<<"请输入顶点数和边数:"<<endl;
    cin>>G.vexnum>>G.edgenum;
    cout<<"请输入顶点信息:"<<endl;
    for(i=0;i<G.vexnum;i++)//输入顶点信息，存入顶点信息数组
		cin>>G.Vex[i].data;
    for(i=0;i<G.vexnum;i++)
        G.Vex[i].first=NULL;
    cout<<"请依次输入每条边的两个顶点u,v"<<endl;
    while(G.edgenum--){
        cin>>u>>v;
        i=locatevex(G,u);//查找顶点u的存储下标
        j=locatevex(G,v);//查找顶点v的存储下标
        if(i!=-1&&j!=-1){
            insertedge(G,i,j);
            insertedge(G,j,i);//无向图多插入一条边
        }
        else{
			cout<<"输入顶点信息错！请重新输入！"<<endl;
			G.edgenum++;//本次输入不算
        }
    }
}

void DFS_AL(ALGraph G,int v){//基于邻接表的深度优先遍历
    int w;
    AdjNode *p;
    cout<<G.Vex[v].data<<"\t";
    visited[v]=true;
    p=G.Vex[v].first;
    while(p){//依次检查v的所有邻接点
		w=p->v;//w为v的邻接点
		if(!visited[w])//w未被访问
       		DFS_AL(G,w);//从w出发，递归深度优先遍历
		p=p->next;
    }
}

void DFS_AL(ALGraph G){//非连通图，基于邻接表的深度优先遍历
    for(int i=0;i<G.vexnum;i++)//非连通图需要查漏点，检查未被访问的顶点
    	if(!visited[i])//i未被访问,以i为起点再次深度优先遍历
       		DFS_AL(G,i);
}

int main(){
    ALGraph G;
    int v;
    VexType c;
    CreateALGraph(G);//创建无向图的邻接表
    printg(G);//输出邻接表
    cout<<"请输入遍历连通图的起始点：";
	cin>>c;
	v=locatevex(G,c);//查找顶点u的存储下标
    if(v!=-1){
        cout<<"深度优先搜索遍历连通图结果："<<endl;
        DFS_AL(G,v);
    }
    else
        cout<<"输入顶点信息错！请重新输入！"<<endl;
    return 0;
}
/*测试数据 
8 9
1 2 3 4 5 6 7 8
1 3
1 2
2 6
2 5
2 4
3 8
3 7
4 5
7 8
1
*/