文章目录
PT@一维连续型分布#均匀分布#指数分布#柯西分布#正态分布及其标准化
- 从概率密度函数很分布函数的角度描述
- 这一点和离散型随机变量的分布用分布律描述有所区别
均匀分布🎈
-
Uniformly Distribution
-
f ( x ) = { 1 b − a , a ⩽ x ⩽ b 0 , e l s e F ( x ) = { 1 , x > b 1 b − a ( x − a ) , a ⩽ x ⩽ b 0 , x < a f(x)= \begin{cases} \frac{1}{b-a},&a\leqslant x \leqslant b \\0,&else \end{cases} \\F(x)= \begin{cases} 1,&x>b \\\frac{1}{b-a}{(x-a)},&a\leqslant x\leqslant b \\0,&x<a \end{cases} f ( x ) = { b − a 1 , 0 , a ⩽ x ⩽ b e l se F ( x ) = ⎩ ⎨ ⎧ 1 , b − a 1 ( x − a ) , 0 , x > b a ⩽ x ⩽ b x < a
- X 服从区间 [ a , b ] 上的均匀分布 X服从区间[a,b]上的均匀分布 X 服从区间 [ a , b ] 上的均匀分布
- 记为 X ∼ U ( a , b ) 记为X\sim U(a,b) 记为 X ∼ U ( a , b )
- X 服从区间 [ a , b ] 上的均匀分布 X服从区间[a,b]上的均匀分布 X 服从区间 [ a , b ] 上的均匀分布
性质
- 等可能性:
- 对于任意一个区间 [ c , c + l ] ⊂ [ a , b ] [c,c+l]\sub [a,b] [ c , c + l ] ⊂ [ a , b ]
- P ( c ⩽ X ⩽ c + l ) = ∫ c c + l f ( x ) d x = 1 b − a ( x − a ) ∣ c c + l = l b − a P(c\leqslant X\leqslant c+l)=\int_{c}^{c+l}f(x)dx=\frac{1}{b-a}{(x-a)}|_{c}^{c+l}=\frac{l}{b-a} P ( c ⩽ X ⩽ c + l ) = ∫ c c + l f ( x ) d x = b − a 1 ( x − a ) ∣ c c + l = b − a l
- 发现,这是一个和区间长度有关,而与区间的起点和终点无关(只要区间位是[a,b]的子区间)
- 或者说:
- 设 X ∼ U [ a , b ] , 则对 a ⩽ c < d ⩽ b X\sim{U[a,b]},则对a\leqslant{c}<d\leqslant{b} X ∼ U [ a , b ] , 则对 a ⩽ c < d ⩽ b
- P ( c < X ⩽ d ) = d − c b − a P(c<X\leqslant{d})=\frac{d-c}{b-a} P ( c < X ⩽ d ) = b − a d − c
- 随机变量落入区间[c,d]的概率等于该区间长度与[a,b]的长度之比
- 对于任意一个区间 [ c , c + l ] ⊂ [ a , b ] [c,c+l]\sub [a,b] [ c , c + l ] ⊂ [ a , b ]
例
-
已知X服从[0,5]上的均匀分布
-
即 X ∼ U ( 0 , 5 ) 即X\sim U(0,5) 即 X ∼ U ( 0 , 5 )
- 如果待求区间概率有落在[0,5]之外的部分,那么这些区间的概率为0
- 实际计算中,只要把被求区间和[0,5]取交,非空的部分分别相加,其余按0计
-
计算 P ( X ⩽ − 1 ∪ X ⩾ 2 ) = P ( X ⩽ − 1 ) + P ( X ⩾ 2 ) 计算P(X\leqslant -1 \cup X\geqslant 2)=P(X\leqslant -1)+P(X\geqslant 2) 计算 P ( X ⩽ − 1 ∪ X ⩾ 2 ) = P ( X ⩽ − 1 ) + P ( X ⩾ 2 )
-
其中 , 和 [ 0 , 5 ] 的交集非空的部分是 [ 2 , 5 ] 其中,和[0,5]的交集非空的部分是[2,5] 其中 , 和 [ 0 , 5 ] 的交集非空的部分是 [ 2 , 5 ]
-
P ( X ⩽ − 1 ∪ X ⩾ 2 ) = P ( 2 ⩽ X ⩽ 5 ) = 1 5 − 0 ( ( 5 − 0 ) − ( 2 − 0 ) ) = 3 5 P(X\leqslant -1 \cup X\geqslant 2) =P(2\leqslant X\leqslant 5) \\=\frac{1}{5-0}((5-0)-(2-0)) =\frac{3}{5} P ( X ⩽ − 1 ∪ X ⩾ 2 ) = P ( 2 ⩽ X ⩽ 5 ) = 5 − 0 1 (( 5 − 0 ) − ( 2 − 0 )) = 5 3
-
-
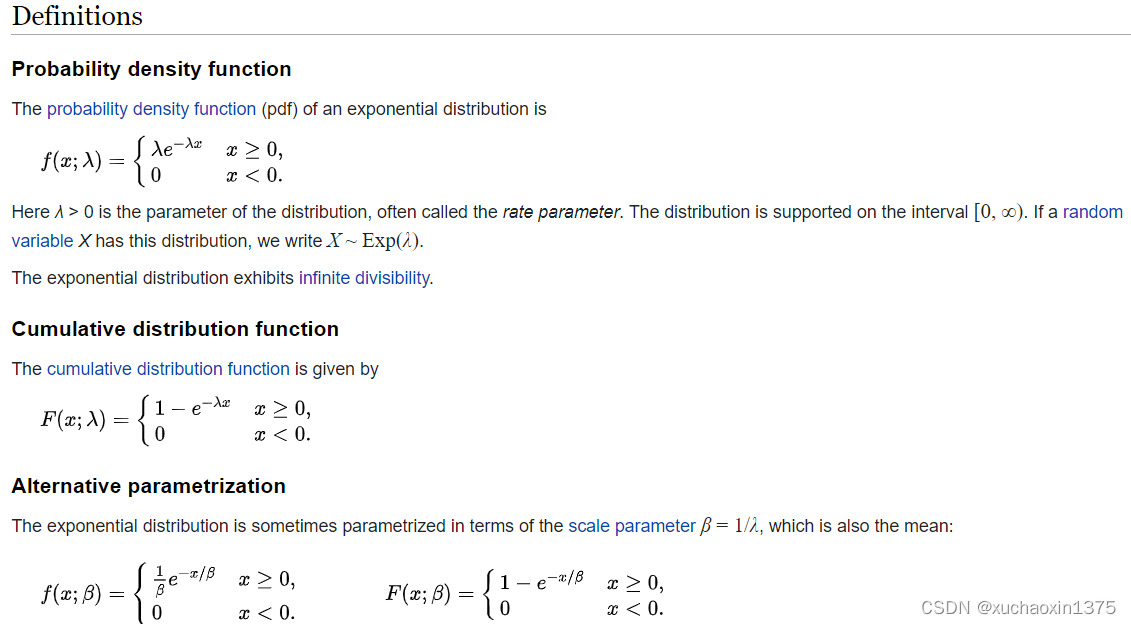
指数分布
-
f ( x ) = { λ e − λ x , x ⩾ 0 0 , x < 0 λ > 0 f(x)= \begin{cases} \lambda e^{-\lambda x},&x\geqslant0 \\0, & x<0 \end{cases} \\\lambda>0 f ( x ) = { λ e − λ x , 0 , x ⩾ 0 x < 0 λ > 0
-
∫ − ∞ x f ( x ) d x = ∫ 0 x λ e − λ x d x = λ ∫ 0 x ( e − λ ) x d x = λ e − λ x ( ln e − λ ) − 1 ∣ 0 x = λ e − λ x 1 − λ ∣ 0 x = − e − λ x ∣ 0 x = − ( e − λ x − 1 ) = 1 − e − λ x \int_{-\infin}^{x}f(x)dx =\int_{0}^{x}\lambda e^{-\lambda x}dx =\lambda \int_{0}^{x}(e^{-\lambda})^{x}dx =\left.\lambda e^{-\lambda x}(\ln e^{-\lambda })^{-1}\right|_{0}^{x} \\=\left.\lambda e^{-\lambda x}\frac{1}{-\lambda}\right|_{0}^{x} = \left.-e^{-\lambda x}\right|_{0}^{x} =-(e^{-\lambda x}-1) =1-e^{-\lambda x} ∫ − ∞ x f ( x ) d x = ∫ 0 x λ e − λ x d x = λ ∫ 0 x ( e − λ ) x d x = λ e − λ x ( ln e − λ ) − 1 0 x = λ e − λ x − λ 1 0 x = − e − λ x 0 x = − ( e − λ x − 1 ) = 1 − e − λ x
-
F ( x ) = { 1 − e − λ x , x ⩾ 0 0 , x < 0 ( λ > 0 ) F(x)= \begin{cases} 1-e^{-\lambda x},&x\geqslant 0 \\0,&x<0 \end{cases} \quad(\lambda>0) F ( x ) = { 1 − e − λ x , 0 , x ⩾ 0 x < 0 ( λ > 0 )
-
-
X服从参数为 λ \lambda λ 的指数分布
- 记为 X ∼ E ( λ ) 记为 X\sim E(\lambda) 记为 X ∼ E ( λ )
性质
无记忆性
-
和离散型分布中的 几何分布 类似的性质,即无记忆性
- 指数分布是连续型分布中唯一具有无记忆性特点
-
推导:
-
如果 X ∼ E ( λ ) X\sim E(\lambda) X ∼ E ( λ )
-
对于任意 t > 0 , s > 0 t>0,s>0 t > 0 , s > 0
-
P ( X > t ) = ∫ t + ∞ λ e − λ t d t = e − λ t , t > 0 P ( X > t ) = 1 − P ( x ⩽ t ) = 1 − P ( x < t ) = 1 − ( 1 − e − λ t ) = e − λ t P(X>t)=\int_{t}^{+\infin}\lambda{e^{-\lambda{t}}}dt=e^{-\lambda{t}},t>0 \\ P(X>t)=1-P(x\leqslant{t})=1-P(x<t)=1-(1-e^{-\lambda{t}})=e^{-\lambda{t}} P ( X > t ) = ∫ t + ∞ λ e − λ t d t = e − λ t , t > 0 P ( X > t ) = 1 − P ( x ⩽ t ) = 1 − P ( x < t ) = 1 − ( 1 − e − λ t ) = e − λ t
-
{ X > t + s } ⊂ { X > s } , 所以 P ( X > t + s ∣ X > s ) = P ( { X > t + s } ∪ { X > s } ) P ( X > s ) = P ( X > s + t ) P ( X > s ) = 1 − P ( X ⩽ s + t ) 1 − P ( X ⩽ s ) = F ( x ) = P ( X ⩽ x ) = 1 − ( 1 − e − λ ( s + t ) ) 1 − ( 1 − e − λ s ) = e − λ ( s + t ) e − λ s = e − λ t \set{X>t+s}\sub\set{X>s},所以 \\ P(X>t+s|X>s)= \frac{P(\set{X>t+s}\cup \set{X>s})}{P(X>s)} =\frac{P(X>s+t)}{P(X>s)} \\=\frac{1-P(X\leqslant s+t)}{1-P(X\leqslant s)} \\\xlongequal{F(x)=P(X\leqslant x)} =\frac{1-(1-e^{-\lambda (s+t)})}{1-(1-e^{-\lambda s})} =\frac{e^{-\lambda (s+t)}}{e^{-\lambda s}} =e^{-\lambda t} { X > t + s } ⊂ { X > s } , 所以 P ( X > t + s ∣ X > s ) = P ( X > s ) P ({ X > t + s } ∪ { X > s }) = P ( X > s ) P ( X > s + t ) = 1 − P ( X ⩽ s ) 1 − P ( X ⩽ s + t ) F ( x ) = P ( X ⩽ x ) = 1 − ( 1 − e − λ s ) 1 − ( 1 − e − λ ( s + t ) ) = e − λ s e − λ ( s + t ) = e − λ t
-
如果某个元件的使用寿命服X服从指数分布:
- 那么该元件已经工作s小时的条件下,还能够再继续工作(剩余)t个小时的概率于s无关
- 但是实际情况元件的剩余寿命往往是和已工作的s小时是有关系的
-
-
ref
例
-
N ( t ) ∼ P ( λ t ) N(t)\sim P(\lambda t) N ( t ) ∼ P ( λ t )
- t 表示时间段长度 t表示时间段长度 t 表示时间段长度
- N ( t ) 表示长度为 t 时间段内发生故障的次数 , 它满足 P o s s i o n 分布 P ( λ t ) N(t)表示长度为t时间段内发生故障的次数,它满足Possion分布P(\lambda t) N ( t ) 表示长度为 t 时间段内发生故障的次数 , 它满足 P oss i o n 分布 P ( λ t )
- P ( N ( t ) = k ) = ( λ t ) k e − ( λ t ) k ! P(N(t)=k)=\frac{(\lambda t)^ke^{-(\lambda t)}}{k!} P ( N ( t ) = k ) = k ! ( λ t ) k e − ( λ t )
- k = 0 时 , P ( N ( t ) = 0 ) = e − ( λ t ) k=0时,P(N(t)=0)=e^{-(\lambda t)} k = 0 时 , P ( N ( t ) = 0 ) = e − ( λ t )
- P ( N ( t ) = k ) = ( λ t ) k e − ( λ t ) k ! P(N(t)=k)=\frac{(\lambda t)^ke^{-(\lambda t)}}{k!} P ( N ( t ) = k ) = k ! ( λ t ) k e − ( λ t )
- T 表示相继 2 次故障之间的时间间隔 T表示相继2次故障之间的时间间隔 T 表示相继 2 次故障之间的时间间隔
-
分析:
- 时间段 t 内出现的故障次数 N ( t ) 如果是 0 次 , 那么可以说明 , 故障间隔 T 一定超过 t ( T > t ) 时间段t内出现的故障次数N(t)如果是0次,那么可以说明,故障间隔T一定超过t(T>t) 时间段 t 内出现的故障次数 N ( t ) 如果是 0 次 , 那么可以说明 , 故障间隔 T 一定超过 t ( T > t )
-
讨论:
-
求:随机变量T的 分布函数F
- 本例中使用分布函数的定义 : F ( x ) = P ( X ⩽ x ) 本例中使用分布函数的定义:F(x)=P(X\leqslant x) 本例中使用分布函数的定义 : F ( x ) = P ( X ⩽ x ) 的方式来求
- 本例中 , 分布函数 F 的自变量为时间段长度 t 本例中,分布函数F的自变量为时间段长度t 本例中 , 分布函数 F 的自变量为时间段长度 t
- 时间轴 t 轴就相当于 x 轴 时间轴t轴就相当于x轴 时间轴 t 轴就相当于 x 轴
- 随机变量T的取值落在t轴的哪个地方
-
一般的,分布函数的定义域为( − ∞ , + ∞ -\infin,+\infin − ∞ , + ∞ )
- 即使我们知道随机变量T只可能落在>0的正区间上,也需要分别讨论一下
-
考虑 t ⩽ 0 考虑t\leqslant0 考虑 t ⩽ 0 :
- 由于 t 时间长度 ( ⩾ 0 ) , 所以 t ⩽ 0 的区间内 , 由于t时间长度(\geqslant0),所以t\leqslant0的区间内, 由于 t 时间长度 ( ⩾ 0 ) , 所以 t ⩽ 0 的区间内 ,
- 事件 { T ⩽ t } 是不可能发生的 事件\set{T\leqslant t}是不可能发生的 事件 { T ⩽ t } 是不可能发生的
- F ( t ) = P ( T ⩽ t ) = 0 F(t)=P(T\leqslant t)=0 F ( t ) = P ( T ⩽ t ) = 0
- 由于 t 时间长度 ( ⩾ 0 ) , 所以 t ⩽ 0 的区间内 , 由于t时间长度(\geqslant0),所以t\leqslant0的区间内, 由于 t 时间长度 ( ⩾ 0 ) , 所以 t ⩽ 0 的区间内 ,
-
t ⩾ 0 t\geqslant 0 t ⩾ 0
-
F ( t ) = P ( T ⩽ t ) = 1 − P ( T > t ) = 1 − P ( N ( t ) = 0 ) = 1 − e − λ t F(t)=P(T\leqslant t)=1-P(T>t)=1-P(N(t)=0)=1-e^{-\lambda t} F ( t ) = P ( T ⩽ t ) = 1 − P ( T > t ) = 1 − P ( N ( t ) = 0 ) = 1 − e − λ t
-
F ( t ) ⩽ { 1 − e − λ t , t ⩾ 0 0 , t < 0 F(t)\leqslant \begin{cases} 1-e^{-\lambda t},&t\geqslant 0 \\0, &t<0 \end{cases} F ( t ) ⩽ { 1 − e − λ t , 0 , t ⩾ 0 t < 0
-
-
柯西分布
-
f ( x ) = 1 π ( 1 + x 2 ) ( − ∞ < x < + ∞ ) F ( x ) = 1 π arctan x + 1 2 f(x)=\frac{1}{\pi(1+x^2)}(-\infin<x<+\infin) \\F(x)=\frac{1}{\pi}\arctan x+\frac{1}{2} f ( x ) = π ( 1 + x 2 ) 1 ( − ∞ < x < + ∞ ) F ( x ) = π 1 arctan x + 2 1
-
用的较少
正态分布
正态密度函数
- f ( x ) = 1 2 π ⋅ σ e − ( x − u ) 2 2 σ 2 ( − ∞ < x < + ∞ ) f(x)=\frac{1}{\sqrt{2\pi}\cdot\sigma}e^{-\frac{(x-u)^2}{2\sigma^2}} \\(-\infin<x<+\infin) f ( x ) = 2 π ⋅ σ 1 e − 2 σ 2 ( x − u ) 2 ( − ∞ < x < + ∞ )
密度函数图像特点
- f ( x ) 关于 x = u 对称 f(x)关于x=u对称 f ( x ) 关于 x = u 对称
- f ( x ) 在 x = u 处有最大值 f ( u ) = ( 2 π σ ) − 1 f(x)在x=u处有最大值f(u)=(\sqrt{2\pi}\sigma)^{-1} f ( x ) 在 x = u 处有最大值 f ( u ) = ( 2 π σ ) − 1
- 从密度函数的形式上也可以看出来 f ( x ) f(x) f ( x ) 关于x=u对称
- f ( x ) = f ( 2 u − x ) 总是成立的 , 因此 f ( x ) 关于 x = u 对称 f(x)=f(2u-x)总是成立的,因此f(x)关于x=u对称 f ( x ) = f ( 2 u − x ) 总是成立的 , 因此 f ( x ) 关于 x = u 对称
- N o t e : x 1 + x 2 = 2 u ; f ( x 1 ) = f ( x 2 ) Note:x_1+x_2=2u;f(x_1)=f(x_2) N o t e : x 1 + x 2 = 2 u ; f ( x 1 ) = f ( x 2 )
- f ( x ) = f ( 2 u − x ) 总是成立的 , 因此 f ( x ) 关于 x = u 对称 f(x)=f(2u-x)总是成立的,因此f(x)关于x=u对称 f ( x ) = f ( 2 u − x ) 总是成立的 , 因此 f ( x ) 关于 x = u 对称
- f ( x ) 在 x = u ± σ 处有拐点 f(x)在x=u\pm \sigma处有拐点 f ( x ) 在 x = u ± σ 处有拐点
- Note:曲线图形的函数在拐点有二阶导数,则二阶导数在拐点处异号(由正变负或由负变正)或不存在
- x → ∞ 时 , 以 x 轴为渐近线 x\to\infin时,以x轴为渐近线 x → ∞ 时 , 以 x 轴为渐近线
正态分布决定性参数@均值@方差
- 如果固定 σ \sigma σ 不变
- 改变 μ \mu μ ,则图形沿着x轴平行移动
- 形状不变
- μ \mu μ 是正态分布密度函数的 位置参数 ,位置是有 μ \mu μ 决定的
- 如果固定 μ \mu μ 不变,
- 改变 σ , 当 σ 变小的时候 , 图形越尖 改变\sigma,当\sigma变小的时候,图形越尖 改变 σ , 当 σ 变小的时候 , 图形越尖
- 否则越扁平
- 因为最大值 f ( u ) = ( 2 π σ ) − 1 因为最大值f(u)=(\sqrt{2\pi}\sigma)^{-1} 因为最大值 f ( u ) = ( 2 π σ ) − 1
- σ 正态分布密度函数的 \sigma 正态分布密度函数的 σ 正态分布密度函数的 尺度参数
这个密度函数 ( 钟型曲线 ) 不易直接积分 , 直接用积分表达式 F ( x ) = 1 2 π σ ∫ − ∞ x e − ( t − u ) 2 2 σ 2 d t \\这个密度函数(钟型曲线)不易直接积分,直接用积分表达式 \\ F(x)=\frac{1}{\sqrt{2\pi}\sigma}\int_{-\infin}^{x}{e^{-\frac{(t-u)^2}{2\sigma^2}}}dt 这个密度函数 ( 钟型曲线 ) 不易直接积分 , 直接用积分表达式 F ( x ) = 2 π σ 1 ∫ − ∞ x e − 2 σ 2 ( t − u ) 2 d t
🎈标准正态分布
-
当 μ = 0 , σ 2 = 1 时 , 当\mu=0,\sigma^2=1时, 当 μ = 0 , σ 2 = 1 时 , 的正态分布为标准正态分布
-
这时候,密度函数和分布函数可以具体为
- f ( x ) = 1 2 π ⋅ σ e − ( x − μ ) 2 2 σ 2 取标准型参数 u = 0 , σ 2 = 1 ϕ ( x ) = 1 2 π e − x 2 2 Φ ( x ) = 1 2 π σ ∫ − ∞ x e − ( t ) 2 2 d t f(x)=\frac{1}{\sqrt{2\pi}\cdot\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}} \\取标准型参数u=0,\sigma^2=1 \\ \phi(x)=\frac{1}{\sqrt{2\pi}}{e^\frac{-x^2}{2}} \\\Phi(x)=\frac{1}{\sqrt{2\pi}\sigma}\int_{-\infin}^{x}{e^{-\frac{(t)^2}{2}}}dt f ( x ) = 2 π ⋅ σ 1 e − 2 σ 2 ( x − μ ) 2 取标准型参数 u = 0 , σ 2 = 1 ϕ ( x ) = 2 π 1 e 2 − x 2 Φ ( x ) = 2 π σ 1 ∫ − ∞ x e − 2 ( t ) 2 d t
3 σ 原则 3\sigma原则 3 σ 原则
-
对于标准正态分布 μ ∼ N ( 0 , 1 ) \mu\sim N(0,1) μ ∼ N ( 0 , 1 )
-
Φ ( − μ ) = 1 − Φ ( μ ) \Phi(-\mu)=1-\Phi(\mu) Φ ( − μ ) = 1 − Φ ( μ )
- 或者 Φ ( μ ) = 1 − Φ ( − μ ) \Phi(\mu)=1-\Phi(-\mu) Φ ( μ ) = 1 − Φ ( − μ )
- Φ ( μ ) + Φ ( − μ ) = 1 \Phi(\mu)+\Phi(-\mu)=1 Φ ( μ ) + Φ ( − μ ) = 1
- P ( μ > μ ) = 1 − P ( μ ⩽ μ ) = 1 − Φ ( μ ) P(\mu>\mu)=1-P(\mu\leqslant \mu)=1-\Phi(\mu) P ( μ > μ ) = 1 − P ( μ ⩽ μ ) = 1 − Φ ( μ )
- P ( a < μ ⩽ b ) = Φ ( b ) − Φ ( a ) P(a<\mu\leqslant b)=\Phi(b)-\Phi(a) P ( a < μ ⩽ b ) = Φ ( b ) − Φ ( a )
- P ( ∣ μ ∣ < c ) = P ( − c < μ < c ) = Φ ( c ) − Φ ( − c ) = Φ ( c ) − ( 1 − Φ ( c ) ) = 2 Φ ( c ) − 1 P(|\mu|<c)=P(-c<\mu<c)=\Phi(c)-\Phi(-c)=\Phi(c)-(1-\Phi(c))=2\Phi(c)-1 P ( ∣ μ ∣ < c ) = P ( − c < μ < c ) = Φ ( c ) − Φ ( − c ) = Φ ( c ) − ( 1 − Φ ( c )) = 2Φ ( c ) − 1
- 或者 Φ ( μ ) = 1 − Φ ( − μ ) \Phi(\mu)=1-\Phi(-\mu) Φ ( μ ) = 1 − Φ ( − μ )
-
P ( ∣ X − μ ∣ < σ ) = Φ ( 1 ) − Φ ( − 1 ) ≈ 0.6826 P ( ∣ X − μ ∣ < 2 σ ) = Φ ( 2 ) − Φ ( − 2 ) ≈ 0.9544 P ( ∣ X − μ ∣ < 3 σ ) = Φ ( 3 ) − Φ ( − 3 ) ≈ 0.9973 表示对于正态分布密度函数两侧距离对称轴 x = μ 不超过 k σ ( k = 1 , 2 , 3 ) 的面积 ( 也即是概率 ) 可以看出 , 如果 X ∼ N ( μ , σ 2 ) , 则 ∣ X − μ ∣ ⩽ 3 σ 的概率相当高 P(|X-\mu|<\sigma)=\Phi(1)-\Phi(-1)\approx0.6826 \\P(|X-\mu|<2\sigma)=\Phi(2)-\Phi(-2)\approx 0.9544 \\P(|X-\mu|<3\sigma)=\Phi(3)-\Phi(-3)\approx 0.9973 \\表示对于正态分布密度函数两侧距离对称轴x=\mu不超过 \\k\sigma(k=1,2,3)的面积(也即是概率) \\可以看出,如果X\sim N(\mu,\sigma^2),则|X-\mu|\leqslant 3\sigma 的概率相当高 P ( ∣ X − μ ∣ < σ ) = Φ ( 1 ) − Φ ( − 1 ) ≈ 0.6826 P ( ∣ X − μ ∣ < 2 σ ) = Φ ( 2 ) − Φ ( − 2 ) ≈ 0.9544 P ( ∣ X − μ ∣ < 3 σ ) = Φ ( 3 ) − Φ ( − 3 ) ≈ 0.9973 表示对于正态分布密度函数两侧距离对称轴 x = μ 不超过 kσ ( k = 1 , 2 , 3 ) 的面积 ( 也即是概率 ) 可以看出 , 如果 X ∼ N ( μ , σ 2 ) , 则 ∣ X − μ ∣ ⩽ 3 σ 的概率相当高
-
一般正态分布标准化
-
一般正态分布:参数为 ( μ , σ 2 ) (\mu,\sigma^2) ( μ , σ 2 ) 的正态分布
-
标准正态分布: μ = 0 , σ 2 = 1 \mu=0,\sigma^2=1 μ = 0 , σ 2 = 1 的正态分布
-
F ( x ) = 1 2 π ⋅ σ ∫ − ∞ x e − ( t − μ ) 2 2 σ 2 d t 积分区域 : t ∈ ( − ∞ , x ] 令 u = u ( t ) = t − μ σ ; t = u σ + μ ; d t = d ( u σ + μ ) = σ d u t − μ ∈ ( − ∞ , x − u ] u = t − μ σ ∈ ( − ∞ , x − μ σ ] 即为换元后的积分区间 F ( x ) = 1 2 π ⋅ σ ∫ − ∞ x − μ σ e − u 2 2 σ d u = 1 2 π ∫ − ∞ x − μ σ e − 1 2 u 2 d u = Φ ( x − μ σ ) 其中 , 函数 Φ 是标准正态分布函数 F ( x ) = Φ ( x − μ σ ) F(x)=\frac{1}{\sqrt{2\pi}\cdot\sigma}\int_{-\infin}^{x}e^{-\frac{(t-\mu)^2}{2\sigma^2}}dt \\积分区域:t\in(-\infin,x] \\ 令u=u(t)=\frac{t-\mu}{\sigma}; \\t=u\sigma+\mu; \\dt=d(u\sigma+\mu)=\sigma{du} \\ t-\mu\in(-\infin,x-u] \\ u=\frac{t-\mu}{\sigma}\in(-\infin,\frac{x-\mu}{\sigma}] 即为换元后的积分区间 \\F(x) =\frac{1}{\sqrt{2\pi}\cdot\sigma}\int_{-\infin}^{\frac{x-\mu}{\sigma}}e^{-\frac{u^2}{2}}\sigma{du} \\=\frac{1}{\sqrt{2\pi}}\int_{-\infin}^{\frac{x-\mu}{\sigma}}e^{-\frac{1}{2}u^2}du \\=\Phi(\frac{x-\mu}{\sigma}) \\其中,函数\Phi是标准正态分布函数 \\F(x)=\Phi(\frac{x-\mu}{\sigma}) F ( x ) = 2 π ⋅ σ 1 ∫ − ∞ x e − 2 σ 2 ( t − μ ) 2 d t 积分区域 : t ∈ ( − ∞ , x ] 令 u = u ( t ) = σ t − μ ; t = u σ + μ ; d t = d ( u σ + μ ) = σ d u t − μ ∈ ( − ∞ , x − u ] u = σ t − μ ∈ ( − ∞ , σ x − μ ] 即为换元后的积分区间 F ( x ) = 2 π ⋅ σ 1 ∫ − ∞ σ x − μ e − 2 u 2 σ d u = 2 π 1 ∫ − ∞ σ x − μ e − 2 1 u 2 d u = Φ ( σ x − μ ) 其中 , 函数 Φ 是标准正态分布函数 F ( x ) = Φ ( σ x − μ )
-
F ( x ) = P ( X ⩽ x ) = Φ ( x − μ σ ) P ( a < X ⩽ b ) = F ( b ) − F ( a ) = Φ ( b − μ σ ) − Φ ( a − μ σ ) F(x)=P(X\leqslant{x})=\Phi(\frac{x-\mu}{\sigma}) \\ P(a<X\leqslant b)=F(b)-F(a)=\Phi(\frac{b-\mu}{\sigma})-\Phi(\frac{a-\mu}{\sigma}) F ( x ) = P ( X ⩽ x ) = Φ ( σ x − μ ) P ( a < X ⩽ b ) = F ( b ) − F ( a ) = Φ ( σ b − μ ) − Φ ( σ a − μ )
- 因此,正态分布都可以用这个一般化的公式(将一般型标准化)计算概率
例
-
如果已知 Y = X − a b ∼ N ( 0 , 1 ) Y=\frac{X-a}{b}\sim{N(0,1)} Y = b X − a ∼ N ( 0 , 1 )
- 其中 μ Y = 0 , σ Y 2 = 1 \mu_Y=0,\sigma^2_Y=1 μ Y = 0 , σ Y 2 = 1
-
则 X = b Y + a X=bY+a X = bY + a
- μ X = b σ Y + a = a ; σ X = b 2 σ Y 2 = b 2 \mu_X=b\sigma_Y+a=a;\sigma_X=b^2\sigma^2_Y=b^2 μ X = b σ Y + a = a ; σ X = b 2 σ Y 2 = b 2
- 即 X ∼ N ( a , b 2 ) X\sim{N(a,b^2)} X ∼ N ( a , b 2 )
一维正态分布性质
-
若 X ∼ N ( 0 , 1 ) X\sim{N(0,1)} X ∼ N ( 0 , 1 ) ,则X的密度函数 ϕ ( x ) \phi(x) ϕ ( x ) ,满足 ϕ ( − x ) = ϕ ( x ) \phi(-x)=\phi(x) ϕ ( − x ) = ϕ ( x ) ,是偶函数
-
当 μ = 0 ( X ∼ N ( 0 , σ ) ) \mu=0(X\sim{N(0,\sigma)}) μ = 0 ( X ∼ N ( 0 , σ ) )
-
F ( a ) + F ( − a ) = 1 ; F ( 0 ) = 1 2 F(a)+F(-a)=1;F(0)=\frac{1}{2} F ( a ) + F ( − a ) = 1 ; F ( 0 ) = 2 1
-
特别地 : Φ ( x ) + Φ ( − x ) = 1 ; Φ ( 0 ) = 1 2 Φ ( x ) 标准正态分布函数 特别地:\\ \Phi(x)+\Phi(-x)=1;\Phi(0)=\frac{1}{2} \\\Phi(x)标准正态分布函数 特别地 : Φ ( x ) + Φ ( − x ) = 1 ; Φ ( 0 ) = 2 1 Φ ( x ) 标准正态分布函数
-
-
当 X ∼ N ( 0 , 1 ) , P ( ∣ X ∣ ⩽ a ) = P ( − a ⩽ X ⩽ a ) = 2 Φ ( a ) − 1 X\sim{N(0,1)},P(|X|\leqslant{a})=P(-a\leqslant{X}\leqslant{a})=2\Phi(a)-1 X ∼ N ( 0 , 1 ) , P ( ∣ X ∣ ⩽ a ) = P ( − a ⩽ X ⩽ a ) = 2Φ ( a ) − 1 ,(a>0)
-
P ( ∣ X ∣ ⩽ a ) = ∫ − a a ϕ ( x ) d x ( = ∫ − ∞ + ∞ ϕ ( x ) d x − ∫ − ∞ − a ϕ ( x ) d x − ∫ a + ∞ ϕ ( x ) d x ) = ∫ − ∞ a ϕ ( x ) d x − ∫ − ∞ − a ϕ ( x ) d x = Φ ( a ) − Φ ( − a ) = Φ ( a ) − ( 1 − Φ ( a ) ) = 2 Φ ( a ) − 1 P(|X|\leqslant{a})=\int_{-a}^{a}\phi(x)dx \\ \left( =\int_{-\infin}^{+\infin}\phi(x)dx -\int_{-\infin}^{-a}\phi(x)dx -\int_{a}^{+\infin}\phi(x)dx \right) \\=\int_{-\infin}^{a}\phi(x)dx-\int_{-\infin}^{-a}\phi(x)dx \\=\Phi(a)-\Phi(-a)=\Phi(a)-(1-\Phi(a))=2\Phi(a)-1 P ( ∣ X ∣ ⩽ a ) = ∫ − a a ϕ ( x ) d x ( = ∫ − ∞ + ∞ ϕ ( x ) d x − ∫ − ∞ − a ϕ ( x ) d x − ∫ a + ∞ ϕ ( x ) d x ) = ∫ − ∞ a ϕ ( x ) d x − ∫ − ∞ − a ϕ ( x ) d x = Φ ( a ) − Φ ( − a ) = Φ ( a ) − ( 1 − Φ ( a )) = 2Φ ( a ) − 1
-
一般正态分布标准化的结论
-
X ∼ ( μ , σ 2 ) X\sim{(\mu,\sigma^2)} X ∼ ( μ , σ 2 ) ,则根据分布函数的定义,计算积分得到
-
F ( x ) = P ( X ⩽ x ) = Φ ( x − μ σ ) P ( a < X ⩽ b ) = F ( b ) − F ( a ) = Φ ( b − μ σ ) − Φ ( a − μ σ ) F(x)=P(X\leqslant{x})=\Phi(\frac{x-\mu}{\sigma}) \\ P(a<X\leqslant b)=F(b)-F(a)=\Phi(\frac{b-\mu}{\sigma})-\Phi(\frac{a-\mu}{\sigma}) F ( x ) = P ( X ⩽ x ) = Φ ( σ x − μ ) P ( a < X ⩽ b ) = F ( b ) − F ( a ) = Φ ( σ b − μ ) − Φ ( σ a − μ )
-
X ∼ ( μ , σ 2 ) X\sim{(\mu,\sigma^2)} X ∼ ( μ , σ 2 ) ,X的分布函数为 F ( x ) = P ( X ⩽ x ) F(x)=P(X\leqslant{x}) F ( x ) = P ( X ⩽ x )
-
令 Y = X − μ σ , 则 Y ∼ ( 0 , 1 ) Y=\frac{X-\mu}{\sigma},则Y\sim{(0,1)} Y = σ X − μ , 则 Y ∼ ( 0 , 1 )
- X = σ Y + μ X=\sigma{Y}+\mu X = σ Y + μ
-
Φ ( y ) = P ( Y ⩽ y ) = P ( X − μ σ ⩽ y ) = P ( X ⩽ y σ + μ ) = F ( y σ + μ ) 令 x = y σ + μ F ( x ) = Φ ( y ) = Φ ( x − μ σ ) \Phi(y)=P(Y\leqslant{y})=P(\frac{X-\mu}{\sigma}\leqslant{y}) \\=P(X\leqslant{y\sigma+\mu})=F(y\sigma+\mu) \\令x=y\sigma+\mu \\F(x)=\Phi(y)=\Phi(\frac{x-\mu}{\sigma}) Φ ( y ) = P ( Y ⩽ y ) = P ( σ X − μ ⩽ y ) = P ( X ⩽ y σ + μ ) = F ( y σ + μ ) 令 x = y σ + μ F ( x ) = Φ ( y ) = Φ ( σ x − μ )
-
另一种推到方法
-
F ( x ) = P ( X ⩽ x ) = P ( X − μ σ ⩽ x − μ σ ) 其中 Y = X − μ σ ∼ ( 0 , 1 ) y = x − μ σ F ( x ) = P ( X ⩽ x ) = P ( Y ⩽ y ) = Φ ( y ) F ( x ) = Φ ( x − μ σ ) F(x)=P(X\leqslant{x})=P(\frac{X-\mu}{\sigma}\leqslant\frac{x-\mu}{\sigma}) \\ 其中Y=\frac{X-\mu}{\sigma}\sim{(0,1)} \\y=\frac{x-\mu}{\sigma} \\ F(x)=P(X\leqslant{x})=P(Y\leqslant{y})=\Phi(y) \\ F(x)=\Phi(\frac{x-\mu}{\sigma}) F ( x ) = P ( X ⩽ x ) = P ( σ X − μ ⩽ σ x − μ ) 其中 Y = σ X − μ ∼ ( 0 , 1 ) y = σ x − μ F ( x ) = P ( X ⩽ x ) = P ( Y ⩽ y ) = Φ ( y ) F ( x ) = Φ ( σ x − μ )
-
-
-