栈的基本概念
栈的定义
限定仅在表尾进行插入或者删除操作的线性表。
- 栈的抽象数据类型描述

栈的顺序存储结构
顺序栈
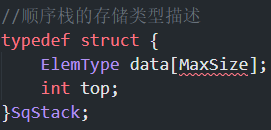
顺序栈的存储类型描述
顺序栈的要素
- 栈顶:
S.top=-1(初始) - 栈空:
S.top==-1 - 栈满:
S.top==MaxSize-1 - 栈长:
S.top+1 - 进栈:
S.data[++S.top]=x; - 出栈:
x=S.data[S.top--];
- 栈顶:
共享栈
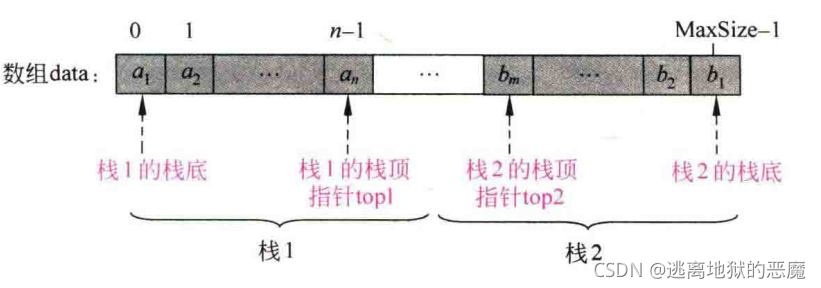
用一个数组来表示两个栈;节省存储空间,降低发生上溢的可能。共享栈的存储结构
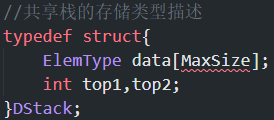
共享栈的存储类型描述
共享栈的要素
- 栈空:栈1空:
top1==-1;栈2空:top2==MaxSize - 栈满:
top1==top2-1 - 进栈:进栈1:
data[++top1]=x;进栈2:data[--top2]=x - 出栈:出栈1:
x=data[top1--];出栈2:x=data[top2++]
- 栈空:栈1空:
栈的链式存储结构
- 链栈
通常使用单链表实现,并规定所有所有操作都在单链表的表头进行。无头结点,Lhead指向栈顶元素。
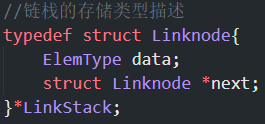
优点:便于多个栈共享存储空间和提高其效率,不存在栈满上溢。链栈的存储类型描述
链栈的要素
- 栈空:
s->next=NULL - 栈满:只有内存溢出时才考虑栈满,通常不考虑,可以看成链栈不存在栈满
- 进栈:类似于链表的头插法
- 出栈:类似于链表删除表头元素
- 栈空:
栈的应用
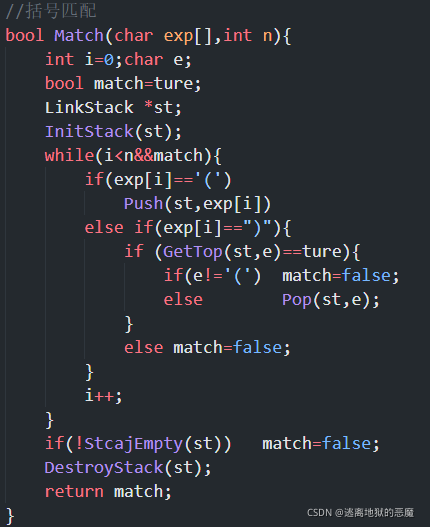
栈在括号匹配中的应用
- 算法实现
栈在表达式求值中的应用
- 算法实现
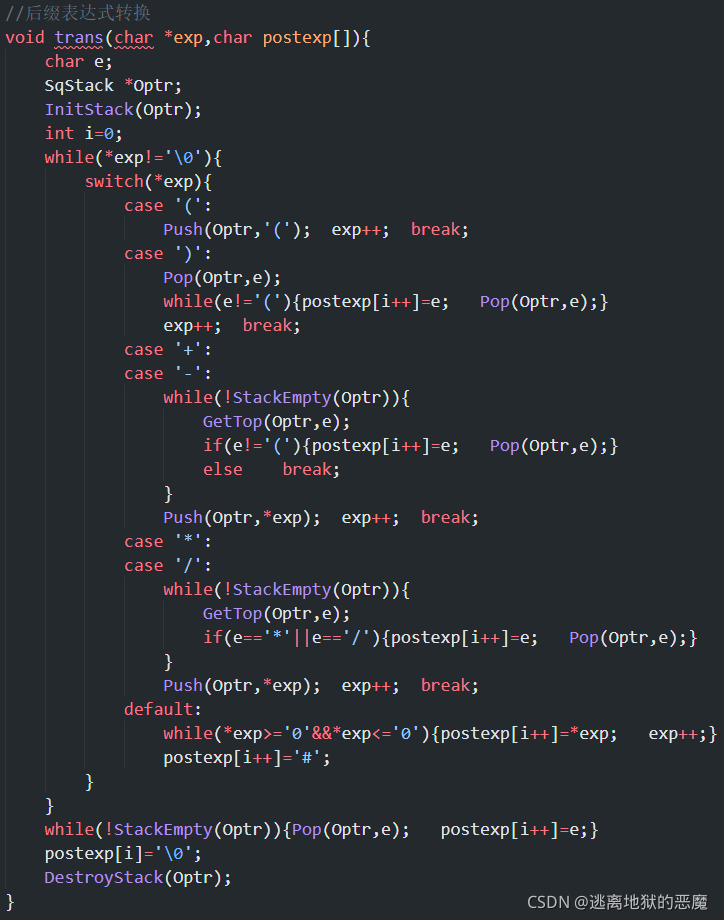
step1:将算式表达式转换成后缀表达式
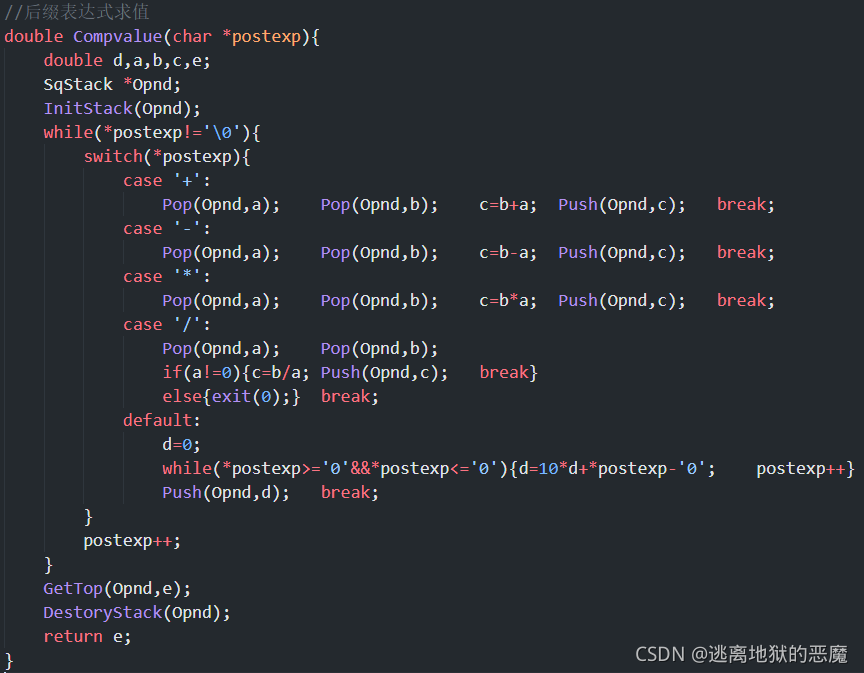
step2:计算后缀表达式的值
栈在递归中的应用
调用函数与被调用函数之间的链接及信息交换需要通过栈来进行.
- Hanoi塔问题

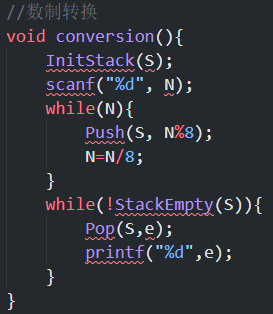
数制转换
- 算法实现
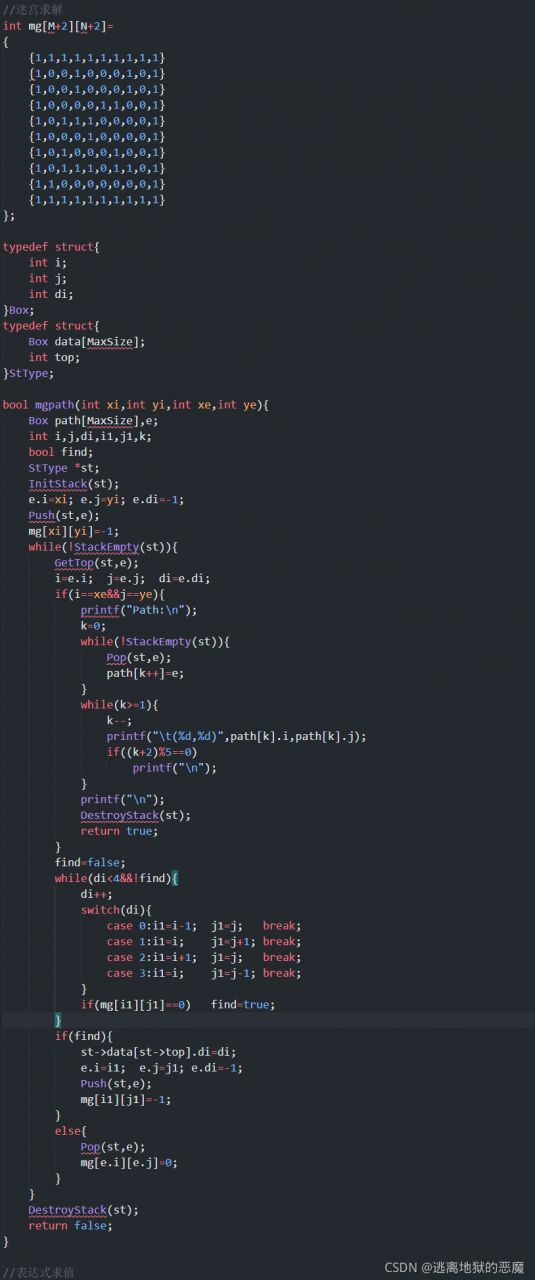
迷宫求解
问题描述

算法简单描述

算法实现
版权声明:本文为qq_43636199原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。