目录
一、判断题
1、将N个数据按照从小到大顺序组织存放在一个单向链表中。如果采用二分查找,那么查找的平均时间复杂度是O(logN)。F
解析:在数组中,这是对的。但是在单向列表中,由于不能通过下标直接访问元素,因此无法进行二分查找。
2、二叉搜索树的查找和折半查找的时间复杂度相同。F
解析:二叉排序树不一定是平衡树,它是只要求了左右子树与根结点存在大小关系,但是对左右子树之间没有层次差异的约束,因此通过二叉排序树进行查找不一定能够满足logn的,例如一棵只有多层左子树的二叉排序树。
只有是一棵平衡的二叉排序树时,其查找时间性能才和折半查找类似。
3、把数组中元素按某种顺序排列的过程叫做查找 。F
解析:“把数组按照某种顺序排列的过程称为排序,而不是称之查找,查找是我们在数组的元素中寻找某个元素的位置,这样的过程称为查找。
4、将M个元素存入用长度为S的数组表示的散列表,则该表的装填因子为M/S。T
解析:哈希表装填因子定义为:α= 填入表中的元素个数/哈希表的长度。
5、在散列中,函数“插入”和“查找”具有同样的时间复杂度。T
解析:插入和查找具有同样的时间复杂度O(1)。
6、在一棵二叉搜索树上查找 63,序列 39、101、25、80、70、59、63 是一种可能的查找时的结点值比较序列。F
解析:
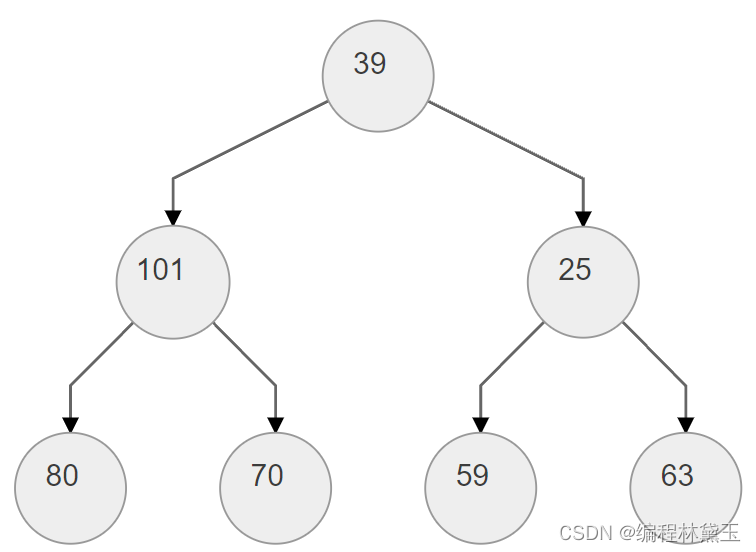
不是二叉搜索树。
7、将 10 个元素散列到 100 000 个单元的哈希表中,一定不会产生冲突。F
解析:有可能会产生冲突,概率不确定。
8、即使把2个元素散列到有100个单元的表中,仍然有可能发生冲突。T
解析:若2个元素的相同散列函数值,则发生冲突。
9、若用平方探测法解决冲突,则插入新元素时,若散列表容量为质数,插入就一定可以成功。F
解析:可能会超出表容量,插入失败。
10、采用平方探测冲突解决策略(hi(k)=(H(k)+i2)%11, 注意:不是±i2),将一批散列值均等于2的对象连续插入一个大小为11的散列表中,那么第4个对象一定位于下标为0的位置。T
解析:第一个地址为2,第二个为2+1,第三个为2+4,第四个为2+9,即下标为0。
二、选择题
1、在下列查找的方法中,平均查找长度与结点个数无关的查找方法是:
A.利用二叉搜索树
B.二分法
C.顺序查找
D.利用哈希(散列)表
解析:由于散列结构是由事先准备好的散列函数关系与处理冲突的方法来确定数据元素在散列表中的存储位置的,因此散列表查找方法的平均查找长度与元素的个数无关。哈希表查找时间复杂度为O(1)。
2、给定散列表大小为11,散列函数为H(Key)=Key%11。采用平方探测法处理冲突:hi(k)=(H(k)±i2)%11将关键字序列{ 6,25,39,61 }依次插入到散列表中。那么元素61存放在散列表中的位置是:
A.6
B.5
C.8
D.7
解析:
6%11=6
25%11=3
39%11=6+1=7
61%11=6-1=5

3、假定有K个关键字互为同义词,若用线性探测法把这K个关键字存入散列表中,至少要进行多少次探测?
A.K+1
B.K−1
C.K
D.K(K+1)/2
解析:K(K+1)/2,其实就是1+2+3+4+......+K。
4、现有长度为 7、初始为空的散列表 HT,散列函数 H(k)=k%7,用线性探测再散列法解决冲突。将关键字 22, 43, 15 依次插入到 HT 后,查找成功的平均查找长度是:
A.1.5
B.2
C.3
D.1.6
解析:

查找22,长度为1;
查找43,长度为2;
查找15,长度为3;
总长度为3;
平均查找长度=(3+2+1)/3=2。
5、将元素序列{18,23,11,20,2,7,27,33,42,15}按顺序插入一个初始为空的、大小为11的散列表中。散列函数为:H(Key)=Key%11,采用线性探测法处理冲突。问:当第一次发现有冲突时,散列表的装填因子大约是多少?
A.0.45
B.0.27
C.0.64
D.0.73
解析:18%11=7
23%11=1
11%11=0
20%11=9
2%11=2
7%11=7+1=8(第一次冲突)
装填因子=5/11=0.45。
6、设有一个已排序的线性表(长度>=2),分别用顺序查找法和二分查找法找一个与K相等的元素,比较的次数分别是S和B,在查找不成功的情况下,S和B的关系是
A.S>=B
B.S<B
C.S>B
D.S=B
解析:设线性表长度为N,S=N;当N=2时,S=B;当N>2时,S>B。
7、散列冲突可以被描述为:
A.两个有不同键值的元素具有相同的散列地址
B.两个有不同数据的元素具有相同的键值
C.两个元素除了有不同键值,其它都相同
D.两个有相同键值的元素具有不同的散列地址
解析:经过散列函数变换后,可能将不同的关键字映射到同一个散列地址上,这种现象称为冲突。
8、在有n(n>1000)个元素的升序数组A中查找关键字x。查找算法的伪代码如下所示:
k = 0;
while ( k<n 且 A[k]<x ) k = k+3;
if ( k<n 且 A[k]==x ) 查找成功;
else if ( k-1<n 且 A[k-1]==x ) 查找成功;
else if ( k-2<n 且 A[k-2]==x ) 查找成功;
else 查找失败;
本算法与二分查找(折半查找)算法相比,有可能具有更少比较次数的情形是:
A.当x接近数组开头处
B.当x位于数组中间位置
C.当x接近数组结尾处
D.当x不在数组中
解析:题中算法为跳跃顺序查找,自然是越靠前越好。
9.给定散列表大小为11,散列函数为H(Key)=Key%11。按照线性探测冲突解决策略连续插入散列值相同的4个元素。问:此时该散列表的平均不成功查找次数是多少?
A.不确定
B.4/11
C.21/11
D.1
解析:(7+5+4+3+2)/11=21/11。
上面的题目均是博主在期末考试前总结的重难点,欢迎各位大佬指正错误或者给出更优质的解析。