一、实验原理

1. 对极几何

对极几何描述的是两视图之间的内存射影关系，同一个三维点在两个不同的视角下的像点存在着约束关系，如下图三维点X在两幅图像的像点分分别为x,x′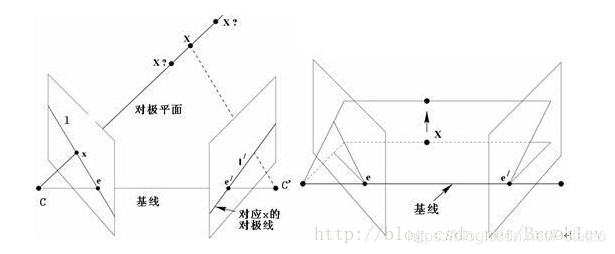

对极几何主要涉及以下几个元素：

基线（Baseline），两个相机中心的连线CC′称为基线
对极点 epipolar ，e,e′是对极点，是基线和两个成像平面的交点，也就是两个相机在另一个成像平面的像点；ee是右边的相机中心C′C′在左边相机的像点，同样e′e′是左边相机中心CC在右边相机的像点。
对极平面 epipolar plane，任何过基线的平面都被才称为对极平面，两个相机的中心C和C′，三维点X，以及其在两个相机的像点x,x′，这5点必定在同一个对极平面上。当三维点X变化时，对极平面绕着基线旋转，形成对极平面束。
对极线 epipolar line ,对极平面和成像平面的交线，所有的对极线相交于极点。
从上面的几何元素可知，对极几何和相机的内参、外参没有关系，和场景的结构也没有关系，仅和场景的一对匹配的像点有关系。

2. 基础矩阵F

给定一对图像（同一场景不同视角得到的图像），从上面的图可知，对于第一幅图像上的任一像点x，在第二幅图像中都有一条与之对应的对极线l′，该对极线是像点x与过第一个相机中心C射线在第二幅图像上的投影，并且第二幅图像中与x相匹配的像点x′必定在该对极线上。因此，存在一个像点x到另一个图像上对极线l′l′的映射： x→l′

基础矩阵F表示的就是这种从点到直线的映射。

基础矩阵的几何推导

要将一幅图像上的像点xx映射到另一幅图像对应的对极线l′l′可以分为两步：第一步，将像点xx映射到另一幅图像上与之对应的对极线l′l′上的某点x′x′上，x′x′是xx的匹配点；第二步，连接对极点e′e′与点x′x′得到的直线就是对极线l′l′。

（1）点通过平面转移

如下图，平面ππ不通过两相机中心，过第一个相机的中心CC和像点xx的射线与ππ相交于点XX。该点XX再投影到第二幅图像上得到像点x′x′,这个过程称为点通过平面的转移。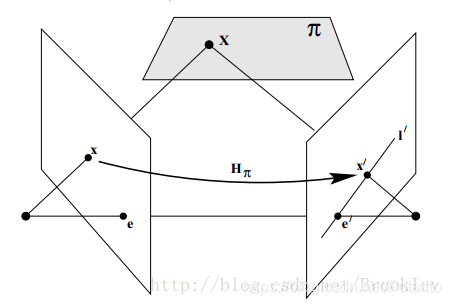

点X位于像点xx和相机中心确定的射线上，其在另一幅图像上的像点x′必然位于该射线在另一幅图像的投影也就是对极线l′上。点xx和点x′都是三维点XX的像点，这样第一副图像上的像点集合xi和第二幅图像上的像点集合x′i是射影等价的，它们都射影等价于共面的三维点集合Xi。因此，存在一个2D单应Hπ，把每一个点xx映射到对应的点x′x′上。

（2） 构造对极线

给点点x′，通过x′和对极点e′的对极线l′l′可以表示为：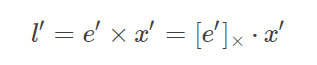

又由于x′=Hπx（Hπ是将xx变换为x′的单应）,带入上式可得：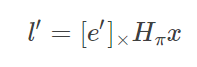

定义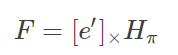

这样就得到了从点x到对极线l′l的变换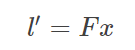

以上就是基础矩阵F的推导过程。

3. 通过匹配点对估算基础矩阵（8点算法）

假设一对匹配的像点p1=[u1,v1,1]T,p2=[u2,v2,1]Tp1=[u1,v1,1]T,p2=[u2,v2,1]T，带入式子中，得到：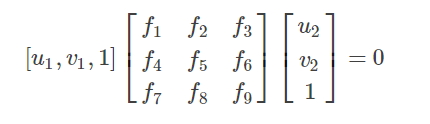

把基础矩阵FF的各个元素当作一个向量处理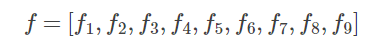

那么上面式子可以写为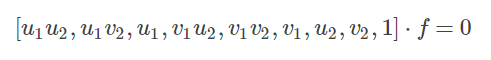

对于其他的点对也使用同样的表示方法。这样将得到的所有方程放到一起，得到一个线性方程组((ui,vi)表示第i个特征点）

求解上面的方程组就可以得到基础矩阵各个元素了。当然这只是理想中的情况，由于噪声、数值的舍入误差和错误的匹配点的影响，仅仅求解上面的线性方程组得到的基础矩阵非常的不稳定，因此在8点法的基础上有各种改进方法。

4. 图像坐标归一化

将上面公式中由匹配的点对坐标组成的矩阵记为系数矩阵A，Af=0，因为矩阵各列的数据尺度差异太大， 最小二乘得到的结果精度一般很低，所以要对各个列向量进行归一化操作。
归一化操作步骤如下

1. 对点进行平移使其形心位于原点。
2. 对点进行缩放，使它们到原点的平均距离为2–√2
3. 对两幅图像独立进行上述变换

设H是归一化的变换矩阵，可记为如下形式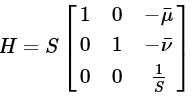

其中，μ¯,ν¯是图像像点坐标两个分量的平均值，S表示尺度，其表达式为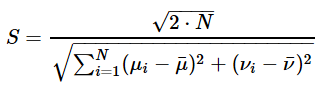

这样，首先对原始的图像坐标进行归一化处理，再利用8点法求解基础矩阵，最后将求得的结果解除归一化，得到基础矩阵F。

5. RANSAC算法

基于匹配点对估算两视图的基础矩阵，唯一的已知条件就是匹配的点对坐标。在实践中，点对的匹配肯定是存在误差的，对于基础矩阵的估算，不匹配的点能够造成很大的误差，即使是只有一对错误的匹配都能使估算值极大的偏离真实值。因此，需要找到一种方法，从包含错误点（外点）的匹配点对集合中，筛选出正确的匹配点（内点）。这时，我们就需要用到RANSAC算法，它的原理之前已经详细阐述过，这里就不再详细说明。

二、代码实现

from PIL import Image
from numpy import *
from pylab import *
import numpy as np

import PCV.geometry.camera as camera
import PCV.geometry.homography as homography
import PCV.geometry.sfm as sfm
import PCV.localdescriptors.sift as sift

im1 = array(Image.open('D:/python/images/test_6/13.jpg'))
sift.process_image('D:/python/images/test_6/13.jpg', 'im13.sift')

im2 = array(Image.open('D:/python/images/test_6/14.jpg'))
sift.process_image('D:/python/images/test_6/14.jpg', 'im14.sift')

l1, d1 = sift.read_features_from_file('im13.sift')
l2, d2 = sift.read_features_from_file('im14.sift')

matches = sift.match_twosided(d1, d2)

ndx = matches.nonzero()[0]
x1 = homography.make_homog(l1[ndx, :2].T)
ndx2 = [int(matches[i]) for i in ndx]
x2 = homography.make_homog(l2[ndx2, :2].T)

d1n = d1[ndx]
d2n = d2[ndx2]
x1n = x1.copy()
x2n = x2.copy()

figure(figsize=(16,16))
sift.plot_matches(im1, im2, l1, l2, matches, True)
show()

def F_from_ransac(x1, x2, model, maxiter=5000, match_threshold=1e-6):
    """ Robust estimation of a fundamental matrix F from point
    correspondences using RANSAC (ransac.py from
    http://www.scipy.org/Cookbook/RANSAC).

    input: x1, x2 (3*n arrays) points in hom. coordinates. """

    import PCV.tools.ransac as ransac
    data = np.vstack((x1, x2))
    d = 10 # 20 is the original
    F, ransac_data = ransac.ransac(data.T, model,
                                   8, maxiter, match_threshold, d, return_all=True)
    return F, ransac_data['inliers']

model = sfm.RansacModel()
F, inliers = F_from_ransac(x1n, x2n, model, maxiter=5000, match_threshold=1e-5)
print F

P1 = array([[1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0]])
P2 = sfm.compute_P_from_fundamental(F)

X = sfm.triangulate(x1n[:, inliers], x2n[:, inliers], P1, P2)


cam1 = camera.Camera(P1)
cam2 = camera.Camera(P2)
x1p = cam1.project(X)
x2p = cam2.project(X)

figure(figsize=(16, 16))
imj = sift.appendimages(im1, im2)
imj = vstack((imj, imj))

imshow(imj)

cols1 = im1.shape[1]
rows1 = im1.shape[0]
for i in range(len(x1p[0])):
    if (0<= x1p[0][i]<cols1) and (0<= x2p[0][i]<cols1) and (0<=x1p[1][i]<rows1) and (0<=x2p[1][i]<rows1):
        plot([x1p[0][i], x2p[0][i]+cols1],[x1p[1][i], x2p[1][i]],'c')
axis('off')
show()

d1p = d1n[inliers]
d2p = d2n[inliers]

# Read features
im3 = array(Image.open('D:/python/images/test_6/15.jpg'))
sift.process_image('D:/python/images/test_6/15.jpg', 'im15.sift')
l3, d3 = sift.read_features_from_file('im15.sift')

matches13 = sift.match_twosided(d1p, d3)

ndx_13 = matches13.nonzero()[0]
x1_13 = homography.make_homog(x1p[:, ndx_13])
ndx2_13 = [int(matches13[i]) for i in ndx_13]
x3_13 = homography.make_homog(l3[ndx2_13, :2].T)

figure(figsize=(16, 16))
imj = sift.appendimages(im1, im3)
imj = vstack((imj, imj))

imshow(imj)

cols1 = im1.shape[1]
rows1 = im1.shape[0]
for i in range(len(x1_13[0])):
    if (0<= x1_13[0][i]<cols1) and (0<= x3_13[0][i]<cols1) and (0<=x1_13[1][i]<rows1) and (0<=x3_13[1][i]<rows1):
        plot([x1_13[0][i], x3_13[0][i]+cols1],[x1_13[1][i], x3_13[1][i]],'c')
axis('off')
show()

P3 = sfm.compute_P(x3_13, X[:, ndx_13])

print P1
print P2
print P3

三、实验结果

1. 左右拍摄，极点位于图像平面上

拍摄数据集如下图：

运行结果：



生成的基础矩阵和三张图的投影矩阵：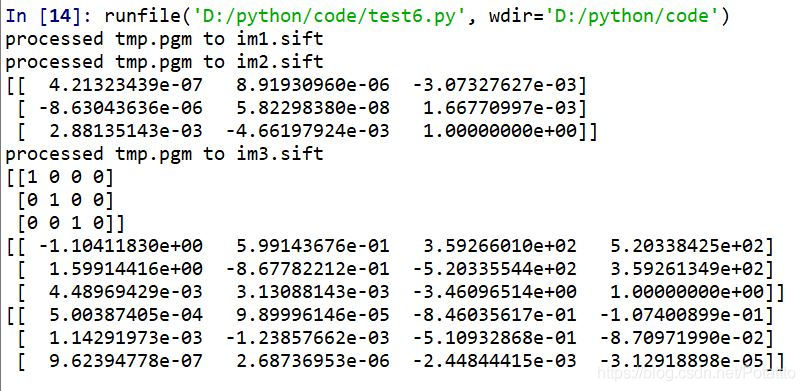

2. 像平面接近平行，极点位于无穷远

拍摄数据集如下图：

运行结果：



生成的基础矩阵和三张图的投影矩阵：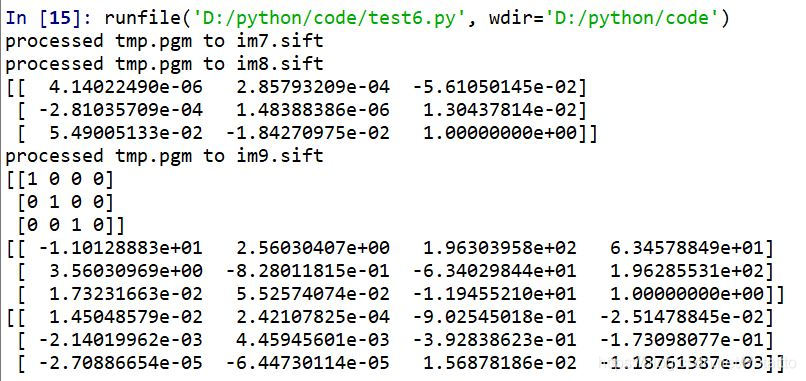

3. 图像拍摄位置位于前后

拍摄数据集如下图：

运行结果：



生成的基础矩阵和三张图的投影矩阵：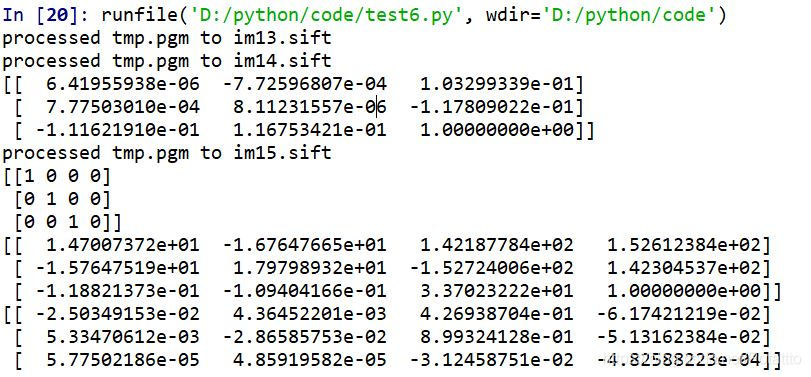

四、 结果分析

1. 根据运行的匹配结果可以发现，左右拍摄和接近平面的两组数据集的匹配效果相比远近不同的数据集要差很多。第一组的图片匹配点较多，但是优化后所剩下的较少，第二张匹配点相对第一组较少，但是优化过后明显特征的匹配点仍被保留。
2. 对于运行后输出的四个矩阵，分别为基础矩阵和三张图片的投影矩阵。对一个包含三幅图像的数据集，计算一对图像中三维点和照相机矩阵，匹配特征到剩下的图像中以获得对应。然后利用对应的三维点使用后方交汇法计算其他图像的照相机矩阵。
3. 错配情况时常发生且没有被剔除，甚至保留了错配很明显的点对而将较好的适配点剔除，这种现象与几乎完全相同的物体结构外观相对应，其中还有因追求时间效率将高分辨率图像进行了压缩处理的影响。
4. 对于较远的目标适配点对数量大，越容易增加错配无法去除的点对数量，对于较近的目标则相反

五、实验中遇到的问题

1. 首先在调试代码以后第一次运行时遇到了下图的报错。经过百度以后发现和数据集中图片的格式有关系。于是对图像进行了再次的处理，但是依旧报错。
   
   之后看到有人说可以调整一下图片顺序，于是在调整完第一组图片的顺序以后成功运行。
2. 但是之后尝试了在室内对桌子上的物体进行拍摄，无论怎么调试都依旧会报错，后来得知RANSAC 的稳健估计对于远近不同的图像集可能会最终遇到无法找到适配点对的情况，需要在调用时多次尝试对阈值（match_threshold=1e-5）进行调整以适用当前图像集。