使用蒙特卡罗方法计算圆周率近似值和定积分
1.实验目的
(1)理解蒙特卡罗方法原理。
(2)熟练使用内置函数input()接收用户输入。
(3)养成对用户输入立即进行类型转换的习惯。
(4)熟练使用for循环控制循环次数。
(5)理解for循环的本质与工作原理。
(6)了解random模块中的常用函数。
2.实验内容
蒙特卡罗方法是一种通过概率统计来得到问题近似解的方法,在很多领域都有重要的应用,其中就包括圆周率近似值的计算问题。假设有一块边长为2的正方形木板,上面画一个单位圆,然后随意往木板上掷飞镖,落点坐标必然在木板上(更多的时候是落在单位圆内),如果掷的次数足够多,那么落在单位圆内的次数除以总次数再乘以4,这个数字会无限逼近圆周率的值。这就是蒙特卡罗发明的用于计算圆周率近似值的方法,如图所示。
(1)计算圆周率近似值
模拟蒙特卡罗计算圆周率近似值的方法,输入掷飞镖次数,然后输出圆周率近似值。观察实验结果,理解实验结果随着模拟次数增多越来越接近圆周率的原因。
from random import uniform
# times = int(input('请输入掷飞镖次数:'))
times=52345
hits = 0
for i in range(times): # 循环
x = uniform(-1, 1) # 产生随机数
y = uniform(-1, 1)
if x*x+y*y <= 1:
hits += 1
print(4.0*hits/times)
结果趋近于3.14
![]()
(2)蒙特卡罗方法求解定积分。
利用蒙特卡罗方法近似计算抛物线y=x2+1,在区间x∈[3, 9],及横轴所围成的图形的面积。
import random
'''
投点法计算函数 y=x^2+1 在[3,9]内的定积分
'''
def f(x):
return x**2 + 1
x1, x2 = 3, 9
y1, y2 = 0, f(x2) # 矩形区域边界
def play_game():
# 在 矩形 区域内随机投点
x = random.uniform(x1, x2) # 均匀分布
y = random.uniform(y1, y2)
# 根据点落在函数 y=x^2图像下方与否,返回1,0(为方便计数)
return [0, 1][y < f(x)]
# 游戏次数
n = 12
# 蒙特卡罗方法,模拟 n 次游戏
integral = sum((play_game() for _ in range(n))) / n # 频率近似于定积分
print((x2-x1)*(y2-y1)*integral)
结果趋近于 240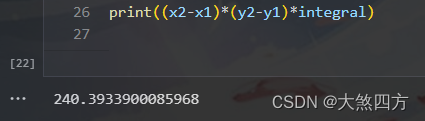










版权声明:本文为qq_52549196原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。