一、遗传算法简介
1.实现
在计算机上模拟生物的进化过程和基因的操作(选择、 交叉、变异)。
2.目的
(1)抽象和严谨地解释自然界的适应过程;
(2)将自然生物系统的重要机理运用到人工系统的设计中。
3.遗传算法概述
遗传算法的基本思想是从初始种群出发,采用优胜劣汰、 适者生存的自然法则选择个体,并通过杂交、变异来产生新 一代种群,如此逐代进化,直到满足目标为止。遗传算法所 涉及到的基本概念主要有以下几个:
• 种群(Population):种群是指用遗传算法求解问题时, 初始给定的多个解的集合。遗传算法的求解过程是从这个子 集开始的。
•个体(Individual):个体是指种群中的单个元素,它通常 由一个用于描述其基本遗传结构的数据结构来表示。例如, 可以用0、1组成的长度为l的串来表示个体。
• 染色体(Chromosome):染色体是指对个体进行编码后 所得到的编码串。染色体中的每1位称为基因,染色体上由 若干个基因构成的一个有效信息段称为基因组。
• 适应度(Fitness)函数:适应度函数是一种用来对种群中 各个个体的环境适应性进行度量的函数。其函数值是遗传 算法实现优胜劣汰的主要依据
• 遗传操作(Genetic Operator):遗传操作是指作用于种 群而产生新的种群的操作。标准的遗传操作包括以下3种基本形式:
– 选择(Selection)
– 杂交(Crosssover)
– 变异(Mutation)
二、基本遗传算法
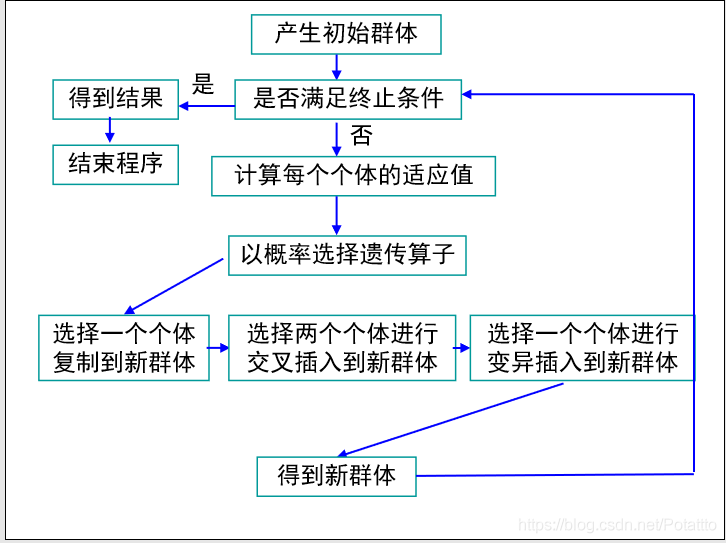
1.编码表示
常用的遗传编码算法有二进制码、实数编码。
(1)二进制编码(Binary encoding)
二进制编码是将原问题的结构变换为染色体的位串结构。在 二进制编码中,首先要确定二进制字符串的长度l,该长度与 变量的定义域和所求问题的计算精度有关。
例 假设变量x的定义域为[4,10],要求的计算精度为10-5, 则需要将[4,10]至少分为600000个等长小区间,每个小区间 用一个二进制串表示。于是,串长至少等于20,原因是: 524288=219<600000<220=1048576 这样,对应于区间[4,10]内满足精度要求的每个值x,都可用 一个20位编码的二进制串<b19,b18,…,b0>来表示。
(2) 实数编码(Real encoding)
实数编码是将每个个体的染色体都用某一范围的一个实 数(浮点数)来表示,其编码长度等于该问题变量的个数。
这种编码方法是将问题的解空间映射到实数空间上,然 后在实数空间上进行遗传操作。由于实数编码使用的是变量 的真实值,因此这种编码方法也叫做真值编码方法。实数编码适应于那种多维、高精度要求的连续函数优化 问题。
2.适应性的度量
个体的适应值即是它繁殖的能力,它将直接 关系到其后代的数量,在遗传算法中,适应 函数是用来区分群体中个体好坏的标准,是 算法演化过程的驱动力,同时也是进行自然 选择的唯一依据。
适应函数
适应值会出现两种情形,一是极小情形即原始适 应值越小个体性能越好;另一种是极大化情形即 原始适应值越大个体性能越好 。
遗传算法中的某些选择策略则要求适应函数是非 负的,而且适应值越大表明个体的性能越好。
对于极小化情形,标准适应值可定义为 :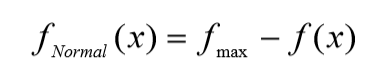
3.选择策略
不同的选择策略将导致不同的选择压力,即下一代 中父代个体的复制数目的不同分配关系。
转盘式选择 (轮赌)
转盘式选择是基于适应值比例的选择中比较重要 的选择策略。 l 先计算个体的相对适应值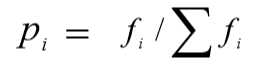
根据选择概率pi把一个圆盘分成N份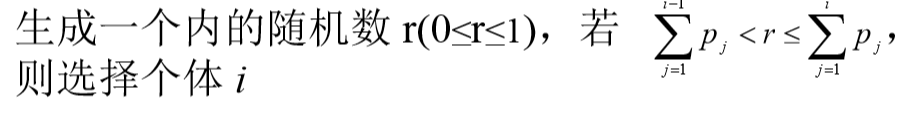
从统计角度看,个体 的适应度值越大,其对 应的扇区的面积越大, 被选中的可能性也越大。这种方法有点类似于发 放奖品使用的轮盘,并 带有某种赌博的意思,因此亦被称为轮盘赌选择。
遗传算子的设计
4.遗传算子的设计
(1)杂交算子
杂交运算是指对两个相互配对的染色体按某种 方式相互交换其部分基因,从而形成两个新的 个体。
① 单点杂交:称为简单杂交,它是指在个体编码 串中只随机设计一个杂交点,然后在该点相互 交换两个配对个体的部分染色体。
② 双点杂交与多点杂交 • 双点杂交是指在个体编码串中设置了二个杂交点, 然后再进行部分基因交换。
③ 均匀杂交 l 均匀杂交是指两个配对个体每一个基因座上的基 因都以相同的杂交概率进行交换,从而形成两个 新的个体。 l 均匀杂交实际上可归属于多点杂交的范围 .
(2)变异算子
变异运算是指将个体染色体编码串中的某些基 因座上的基因值用该基因座的其它等为基因来 替换,从而形成一个新的个体。
遗传算法中使用变异算子主要有以下两个目的: 1)改善遗传算法的局部搜索能力。 2)维持群体的多样性,防止出现早熟现象。
①基本位变异
对个体的每一个基因座,依变异概率Pm指定其为变异点。
对每一个指定的变异点,对其基因值做取反运算 或用其他等位基因值来代替,从而产生出一个新 的个体。
②均匀变异
• 依次指定个体编码串中的每个基因座为变异点。
• 对每一个变异点,以变异概率Pm从对应基因的取值范围内取一随机数来替代原有基因值。
三、函数优化


四、代码实现
1.相关参数
T 仿真代数
N 群体规模
pm pc 交叉变异概率
umax umin 参数取值范围
L 单个参数字串长度
总编码长度Dim*L
Dim维空间搜索
bval=round(rand(N,Dim*L)); 初始种群(round函数为四舍五入)
bestv=-inf; 最优适应度初值
2.相关代码
% Optimizing a function using Simple Genetic Algorithm with elitist preserved
%Max f(x1,x2)=100*(x1*x1-x2).^2+(1-x1).^2; -2.0480<=x1,x2<=2.0480
%下面为代码。函数最大值为3904.9262,此时两个参数均为-2.0480,有时会出现局部极值,此时一个参数为-2.0480,一个为2.0480。变
%异概率pm=0.05,交叉概率pc=0.8。
clc;clear all;
format long;%设定数据显示格式
%初始化参数
T=500;%仿真代数
N=80;% 群体规模
pm=0.05;pc=0.8;%交叉变异概率
umax=30;umin=-30;%参数取值范围
L=10;%单个参数字串长度,总编码长度Dim*L
Dim=5;%Dim维空间搜索
bval=round(rand(N,Dim*L));%初始种群,round函数为四舍五入
bestv=-inf;%最优适应度初值
funlabel=2; %选择待优化的函数,1为Rastrigin,2为Schaffer,3为Griewank
Drawfunc(funlabel);%画出待优化的函数,只画出二维情况作为可视化输出
%迭代开始
for ii=1:T
%解码,计算适应度
for i=1:N %对每一代的第i个粒子
for k=1:Dim
y(k)=0;
for j=1:1:L %从1到L,每次加以1
y(k)=y(k)+bval(i,k*L-j+1)*2^(j-1);%把第i个粒子转化为十进制的值,例如y1是第一维
end
x(k)=(umax-umin)*y(k)/(2^L-1)+umin;%转化为实际的x1
end
% obj(i)=100*(x1*x1-x2).^2+(1-x1).^2; %目标函数
obj(i)=fun(x,funlabel);
xx(i,:)=x;
end
func=obj;%目标函数转换为适应度函数
p=func./sum(func);
q=cumsum(p);%累加
[fmax,indmax]=max(func);%求当代最佳个体
if fmax>=bestv
bestv=fmax;%到目前为止最优适应度值
bvalxx=bval(indmax,:);%到目前为止最佳位串
optxx=xx(indmax,:);%到目前为止最优参数
end
Bfit1(ii)=bestv; % 存储每代的最优适应度
%%%%遗传操作开始
%轮盘赌选择
for i=1:(N-1)
r=rand;
tmp=find(r<=q);
newbval(i,:)=bval(tmp(1),:);
end
newbval(N,:)=bvalxx;%最优保留
bval=newbval;
%单点交叉
for i=1:2:(N-1)
cc=rand;
if cc<pc
point=ceil(rand*(2*L-1));%取得一个1到2L-1的整数
ch=bval(i,:);
bval(i,point+1:2*L)=bval(i+1,point+1:2*L);
bval(i+1,point+1:2*L)=ch(1,point+1:2*L);
end
end
bval(N,:)=bvalxx;%最优保留
%位点变异
mm=rand(N,Dim*L)<pm;%N行
mm(N,:)=zeros(1,Dim*L);%最后一行是精英不变异,强制赋0
bval(mm)=1-bval(mm);
end
%输出
figure;
plot(-Bfit1);% 绘制最优适应度进化曲线
bestv %输出最优适应度值
optxx %输出最优参数
3.结果展示
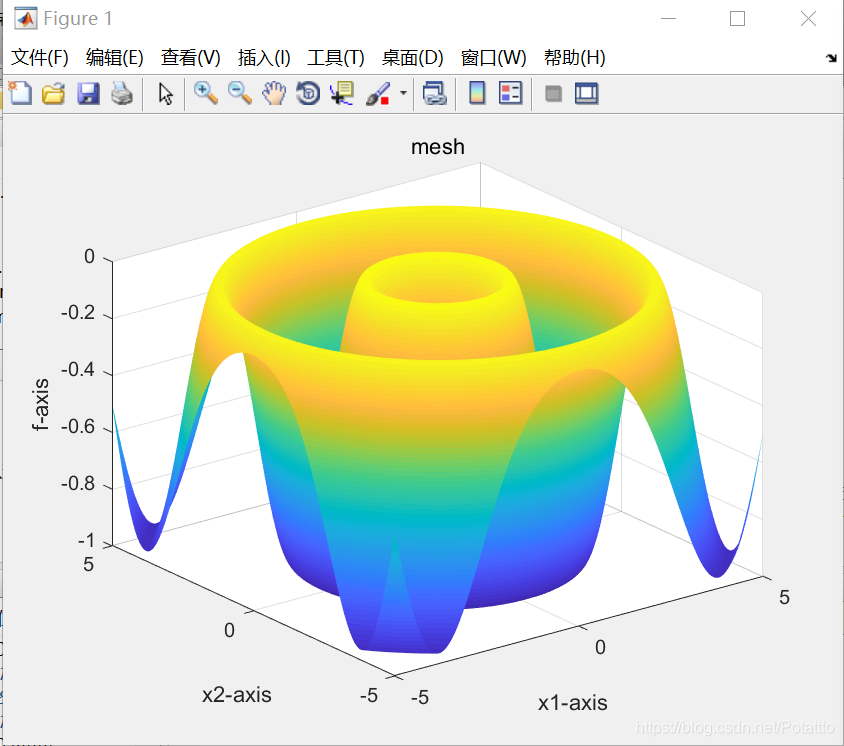
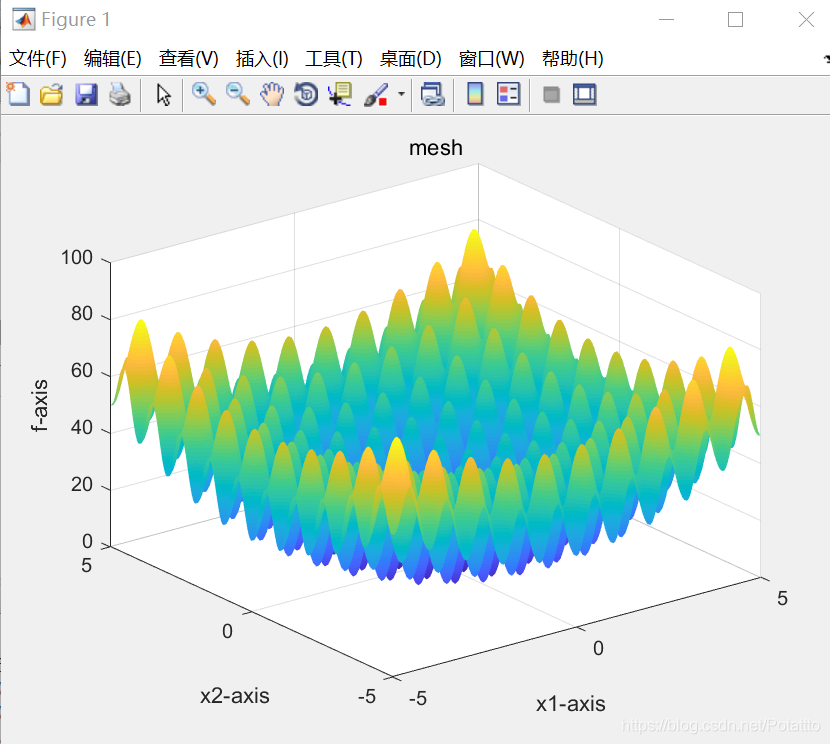
1.对Schaffer函数优化
function y=Schaffer(x)
[row,col]=size(x);
if row>1
error('输入的参数错误');
end
y1=x(1,1);
y2=x(1,2);
temp=y1^2+y2^2;
y=0.5-(sin(sqrt(temp))^2-0.5)/(1+0.001*temp)^2;
y=-y;
(1)种群数量N=80,维度Dim=5:
bestv =
0.990283826870370
optxx =
-3.137829912023459 -0.029325513196483 -2.199413489736070 10.410557184750736 21.085043988269796
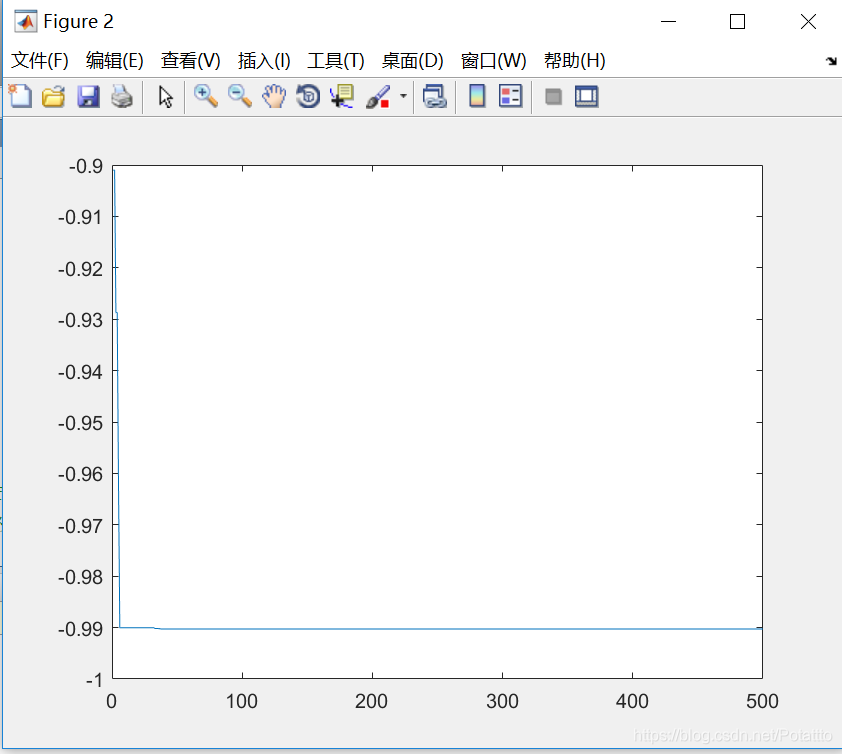
(2)种群数量N=80,维度Dim=2:
输出结果为:
bestv =
0.990283826870370
optxx =
3.020527859237539 0.850439882697948
曲线: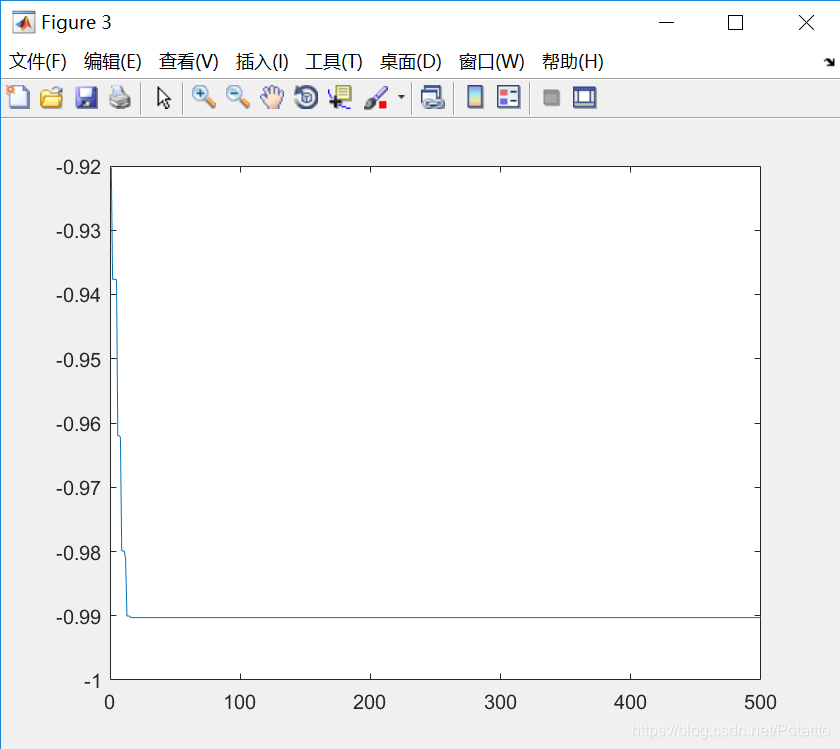
(3)种群数量N=80,维度Dim=10:
输出结果为:
bestv =
0.998279300372192
optxx =
1 至 7 列
-0.029325513196483 -0.029325513196483 3.020527859237539 -6.070381231671554 18.797653958944281 7.067448680351909 17.390029325513197
8 至 10 列
16.158357771260995 19.501466275659823 -15.630498533724341
曲线: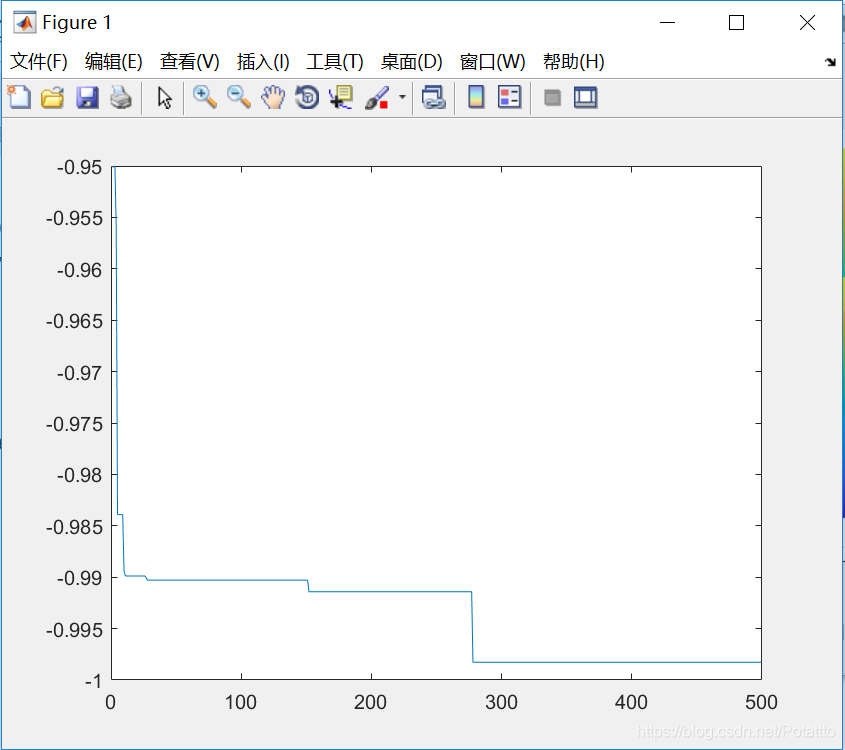
(4)种群数量N=40,维度Dim=5:
bestv =
0.998279300372192
optxx =
-0.029325513196483 0.029325513196483 -8.123167155425222 1.788856304985337 20.674486803519059
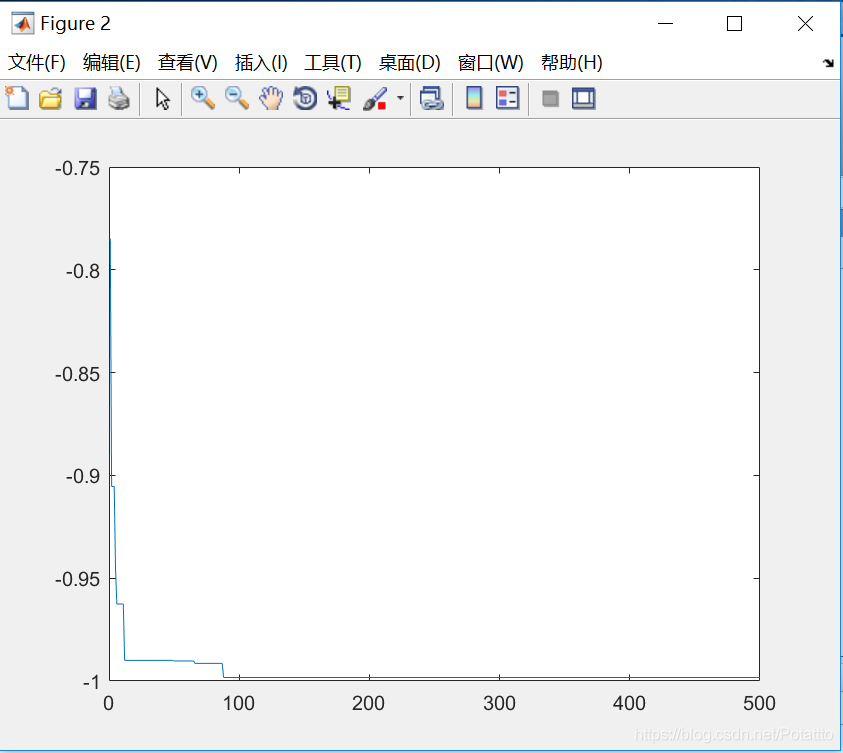
(5)种群数量N=40,维度Dim=2:
bestv =
0.990283826870370
optxx =
-3.020527859237536 0.850439882697948
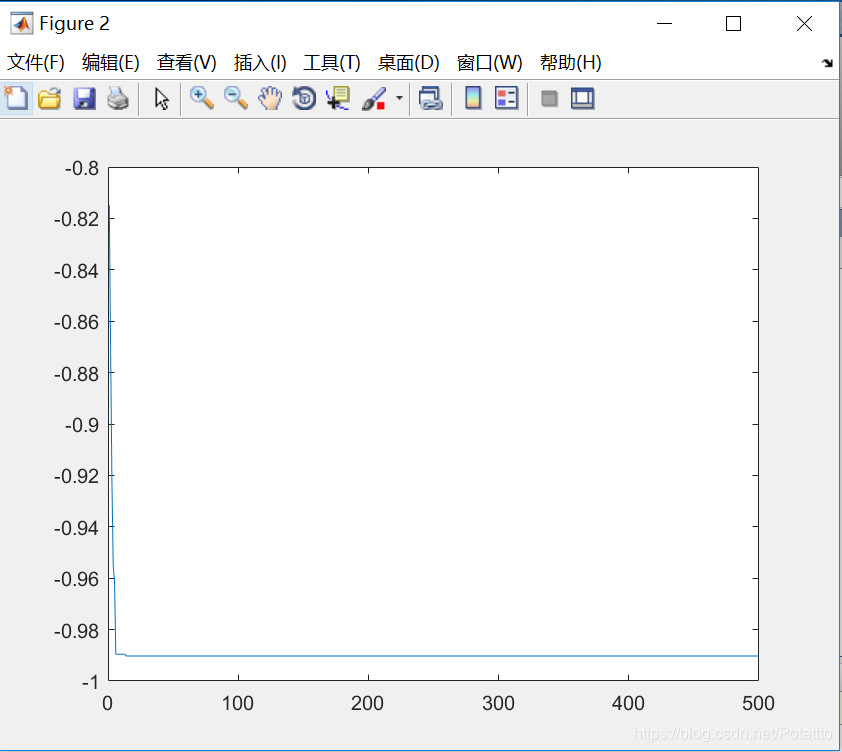
(6)种群数量N=40,维度Dim=10:
bestv =
0.990283762014982
optxx =
1 至 7 列
-2.727272727272727 -1.554252199413490 28.826979472140764 -5.718475073313783 -8.357771260997069 1.495601173020528 13.519061583577709
8 至 10 列
-23.782991202346039 29.824046920821111 1.730205278592376
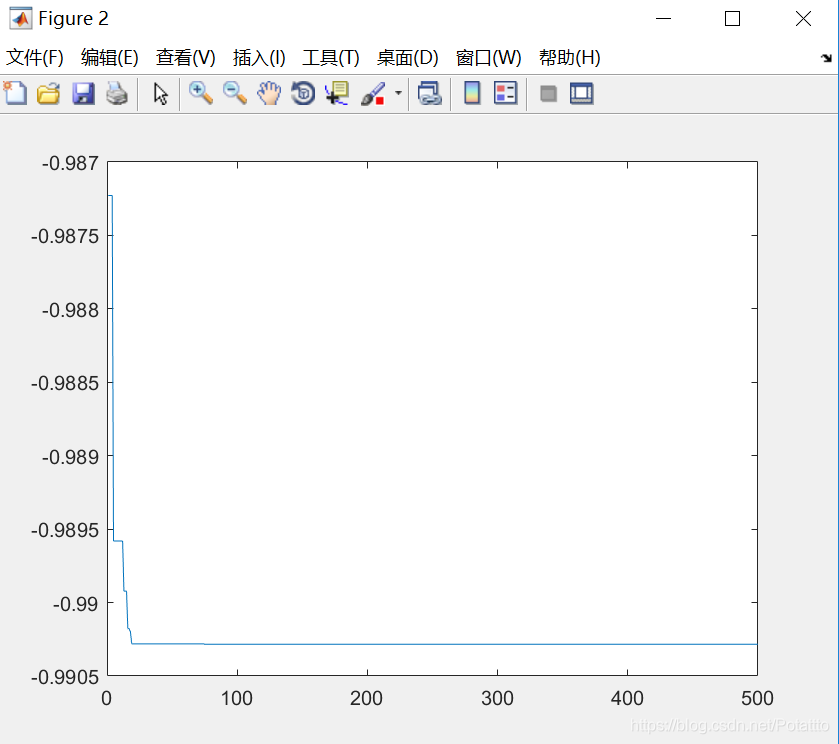
(7)种群数量N=100,维度Dim=5:
bestv =
0.990283826870370
optxx =
1.906158357771261 -2.492668621700879 -4.428152492668623 -4.134897360703814 -2.492668621700879
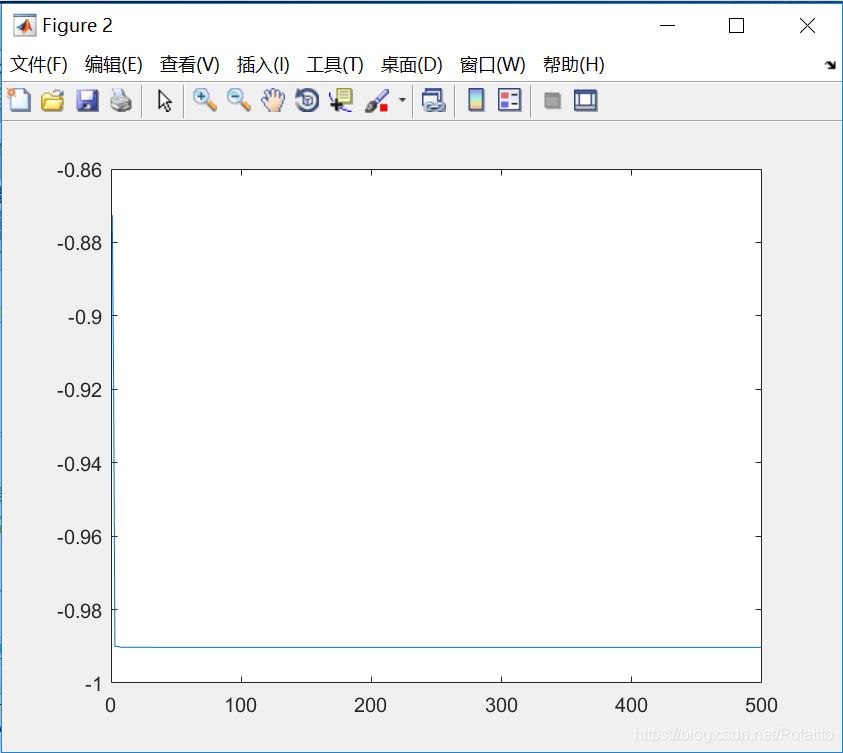
(8)种群数量N=100,维度Dim=2:
bestv =
0.990283826870370
optxx =
3.020527859237539 -0.850439882697948
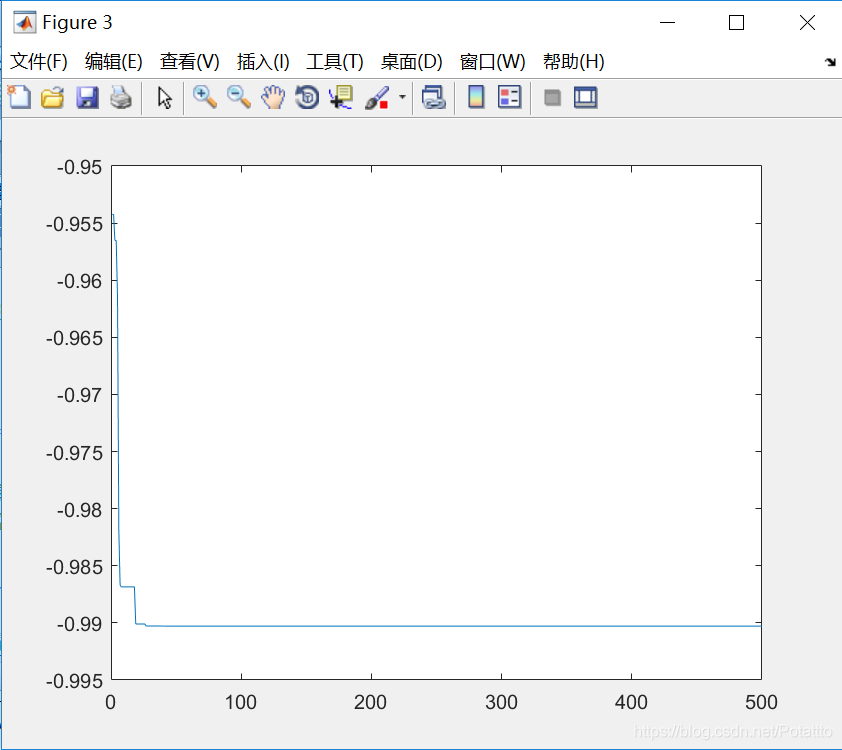
(9)种群数量N=100,维度Dim=10:
bestv =
0.998279300372192
optxx =
1 至 7 列
-0.029325513196483 -0.029325513196483 22.785923753665692 23.607038123167158 7.829912023460409 21.964809384164219 -10.000000000000000
8 至 10 列
19.501466275659823 16.803519061583579 -21.260997067448681
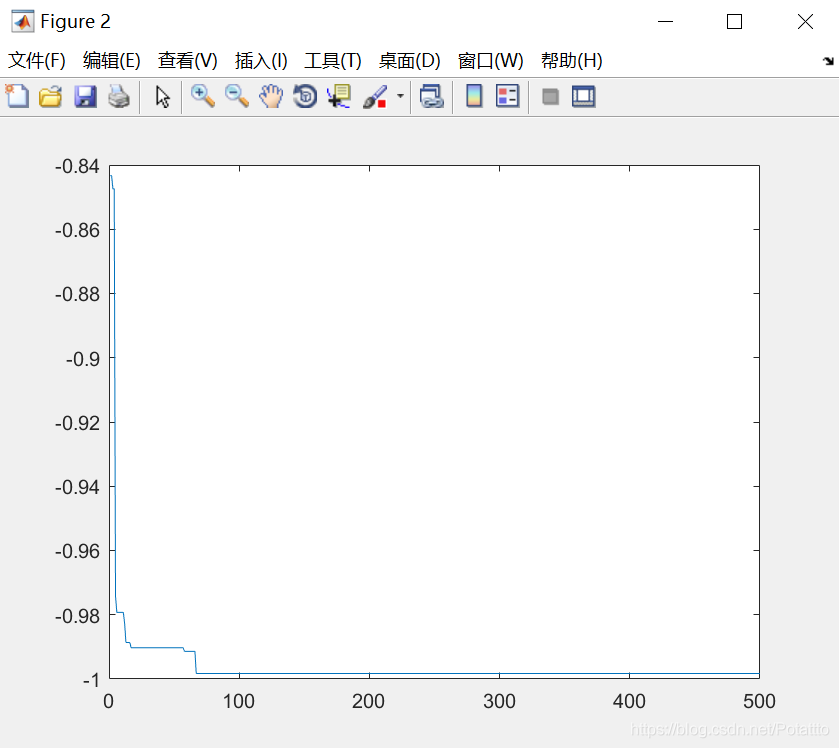
2.对Rastrigin函数优化
函数代码:
function y = Rastrigin(x)
% Rastrigin函数
% 输入x,给出相应的y值,在x = ( 0 , 0 ,…, 0 )处有全局极小点0.
% 编制人:
% 编制日期:
[row,col] = size(x);
if row > 1
error( ' 输入的参数错误 ' );
end
y =sum(x.^2-10*cos(2*pi*x)+10);
%y =-y;
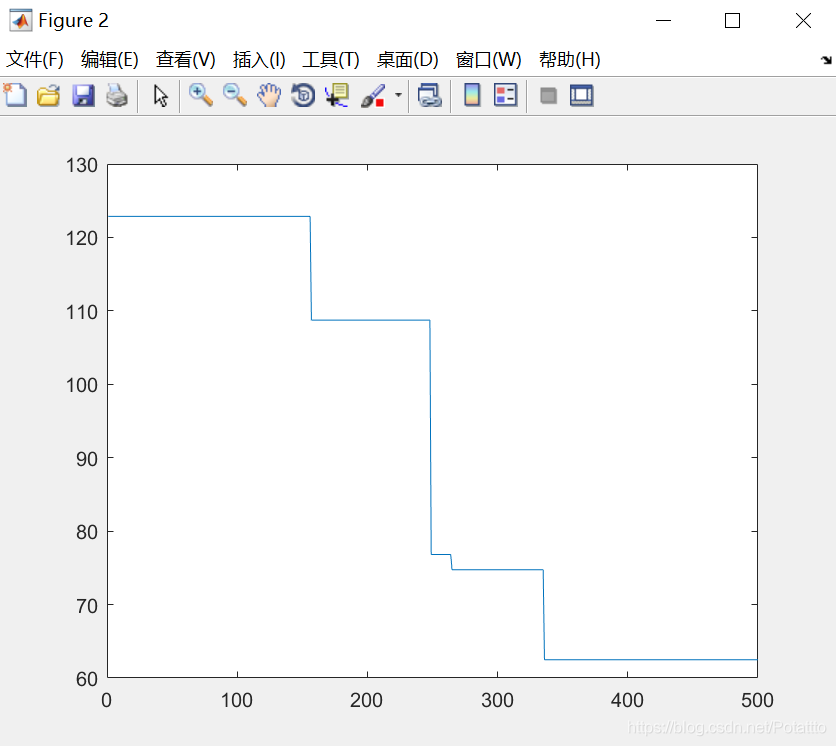
(1)种群数量N=80,维度Dim=5:
bestv =
-62.479602222108497
optxx =
-0.850439882697948 0.439882697947215 -2.199413489736070 2.023460410557185 -3.782991202346039
(2)种群数量N=80,维度Dim=2:
bestv =
-4.274062572600121
optxx =
-0.029325513196483 1.964809384164223
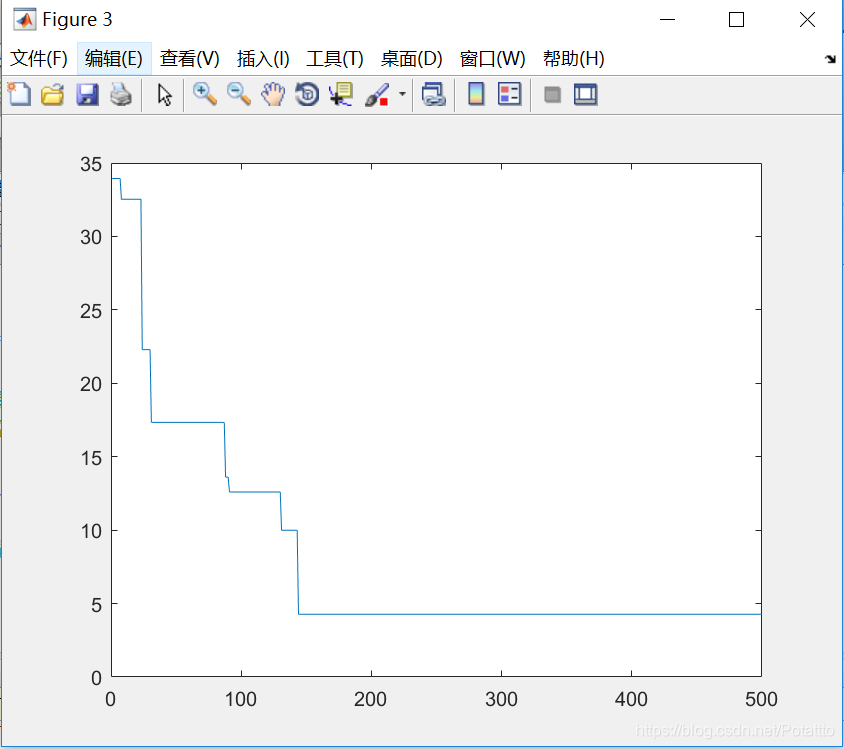
(3)种群数量N=80,维度Dim=10:
bestv =
-5.029817842908374e+02
optxx =
1 至 7 列
-3.782991202346039 -6.950146627565982 -7.829912023460409 3.782991202346039 10.997067448680355 -0.909090909090910 -5.249266862170089
8 至 10 列
10.000000000000000 6.422287390029325 -3.782991202346039
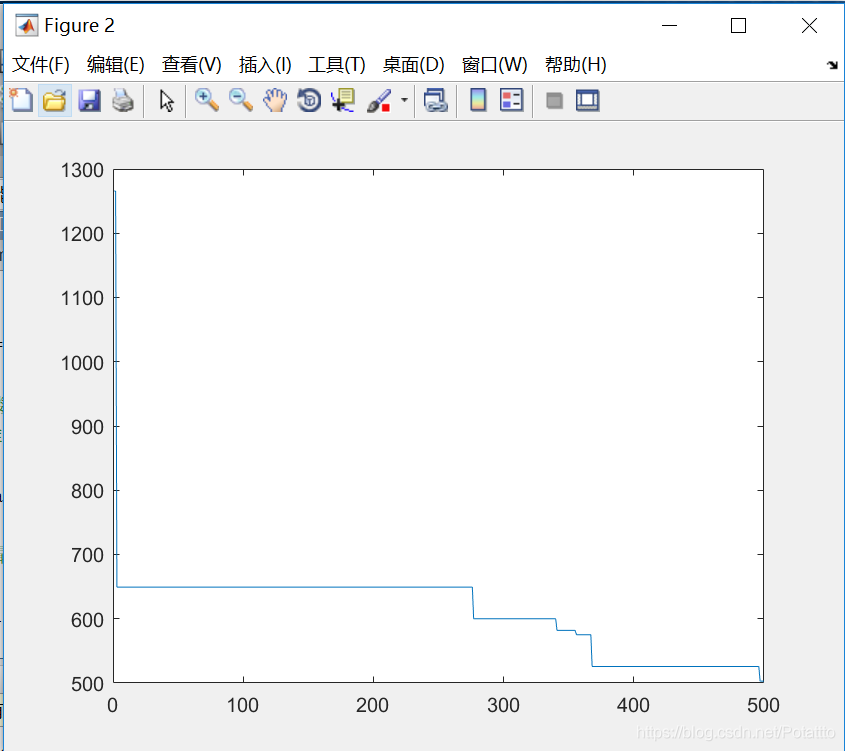
(4)种群数量N=40,维度Dim=5:
bestv =
-1.128024604198187e+02
optxx =
4.428152492668623 2.023460410557185 -1.319648093841643 4.017595307917887 6.070381231671554
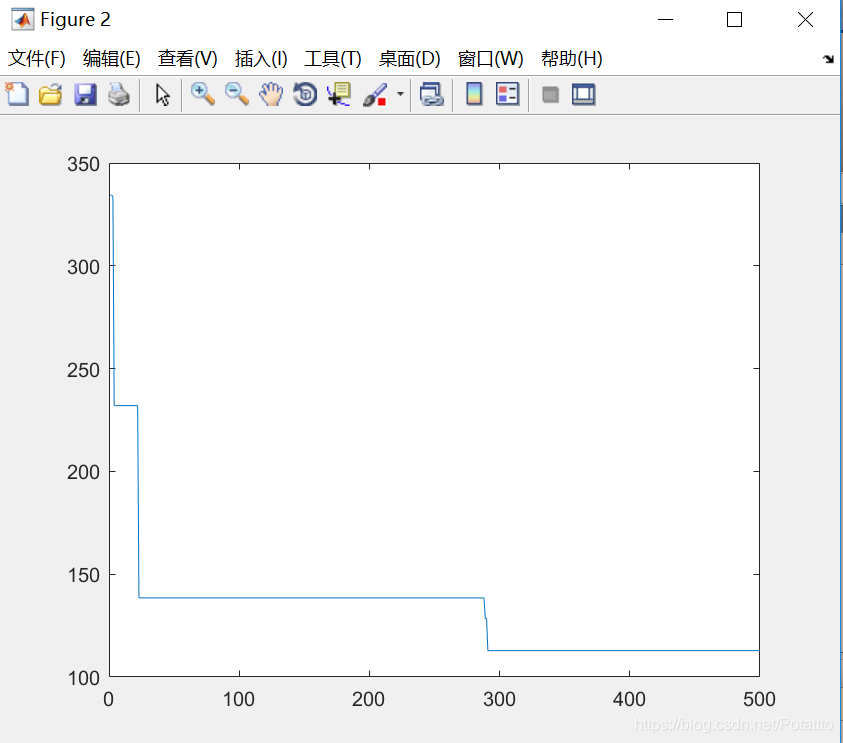
(5)种群数量N=40,维度Dim=2:
bestv =
-1.360803368822516
optxx =
-1.026392961876834 0.029325513196483
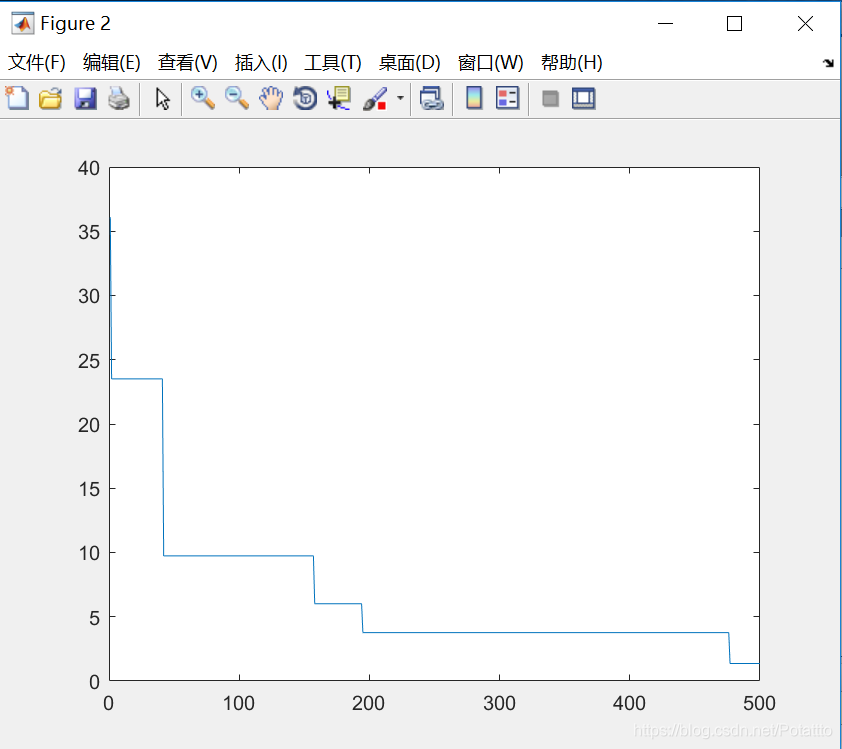
(6)种群数量N=40,维度Dim=10:
bestv =
-2.816915713946689e+02
optxx =
1 至 7 列
4.838709677419352 1.730205278592376 -2.551319648093841 1.964809384164223 0.733137829912025 -7.419354838709676 -1.495601173020528
8 至 10 列
0.263929618768330 -3.137829912023459 -8.240469208211145
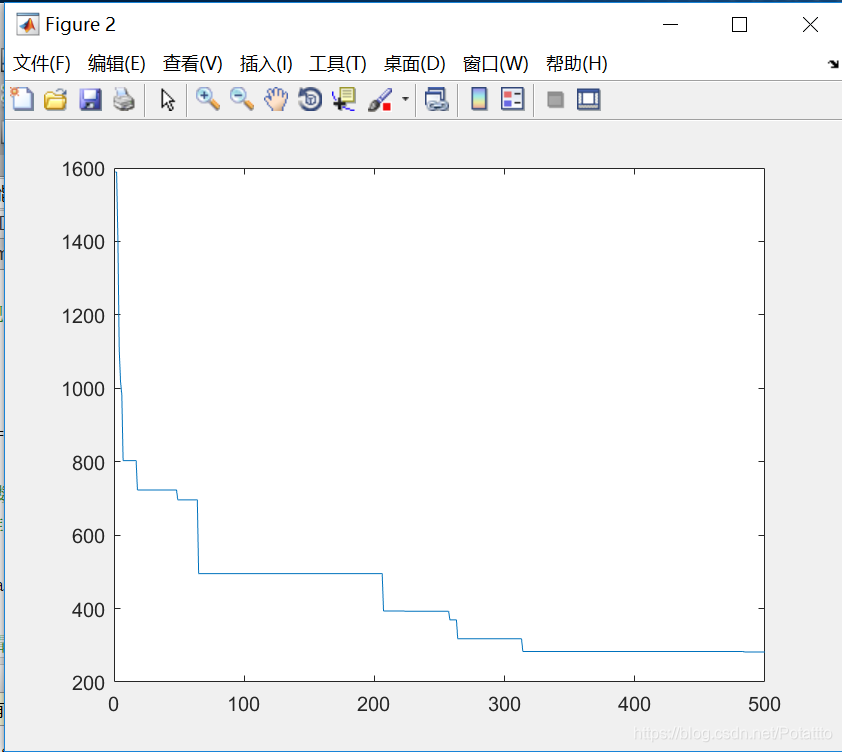
(7)种群数量N=100,维度Dim=5:
bestv =
-1.457406142456419e+02
optxx =
-6.715542521994134 -0.146627565982406 4.956011730205276 -0.615835777126101 -5.307917888563050
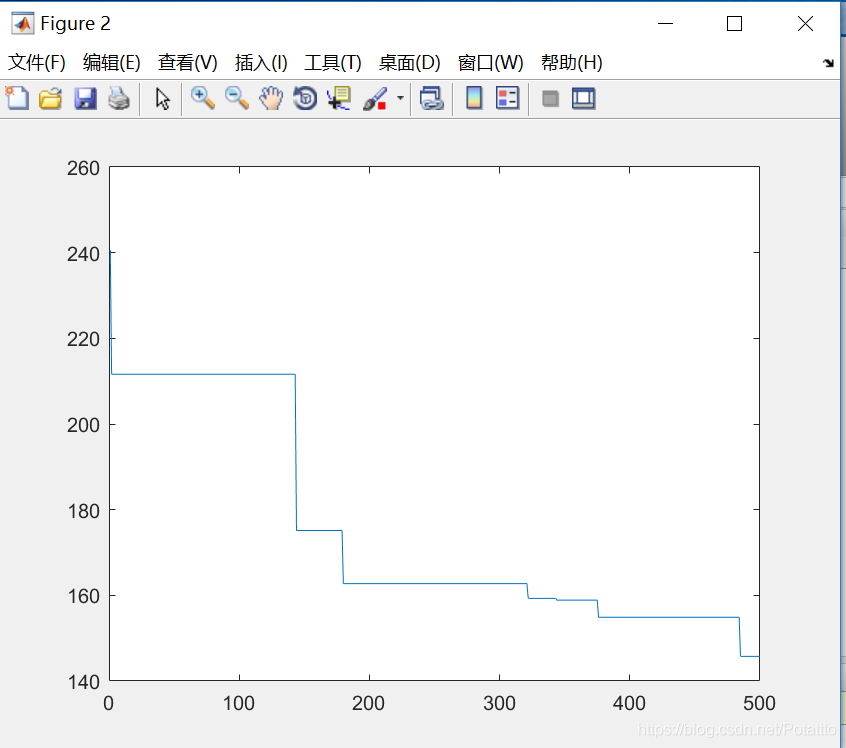
(8)种群数量N=100,维度Dim=2:
bestv =
-1.667155637436144
optxx =
0.087976539589445 0.029325513196483
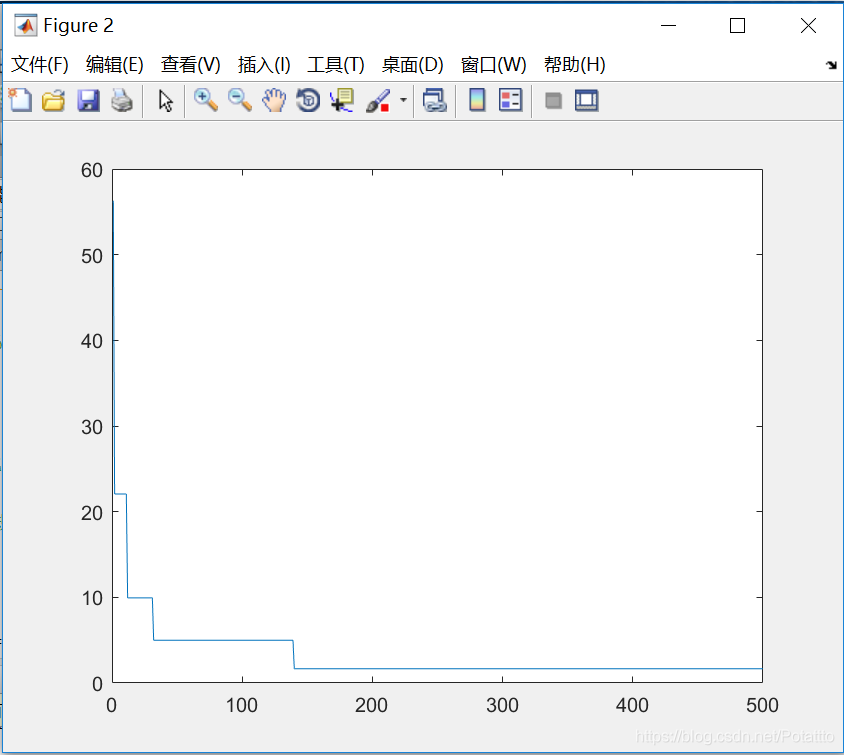
(9)种群数量N=100,维度Dim=10:
bestv =
-3.277187543431874e+02
optxx =
1 至 7 列
0.791788856304986 1.964809384164223 -1.202346041055719 4.193548387096776 8.005865102639298 10.234604105571847 -2.492668621700879
8 至 10 列
-4.076246334310852 2.668621700879768 4.604105571847505
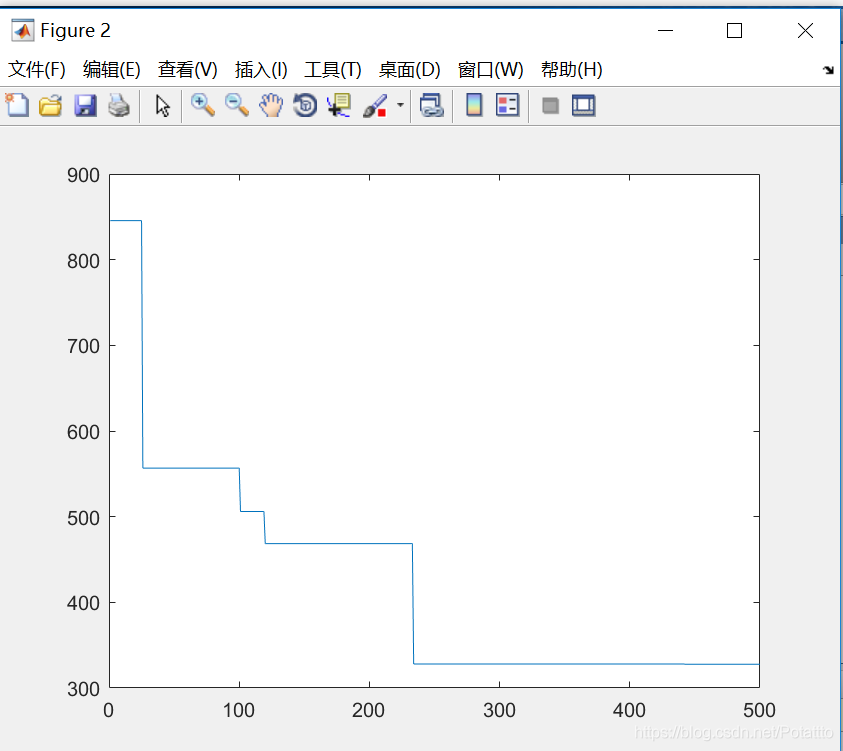
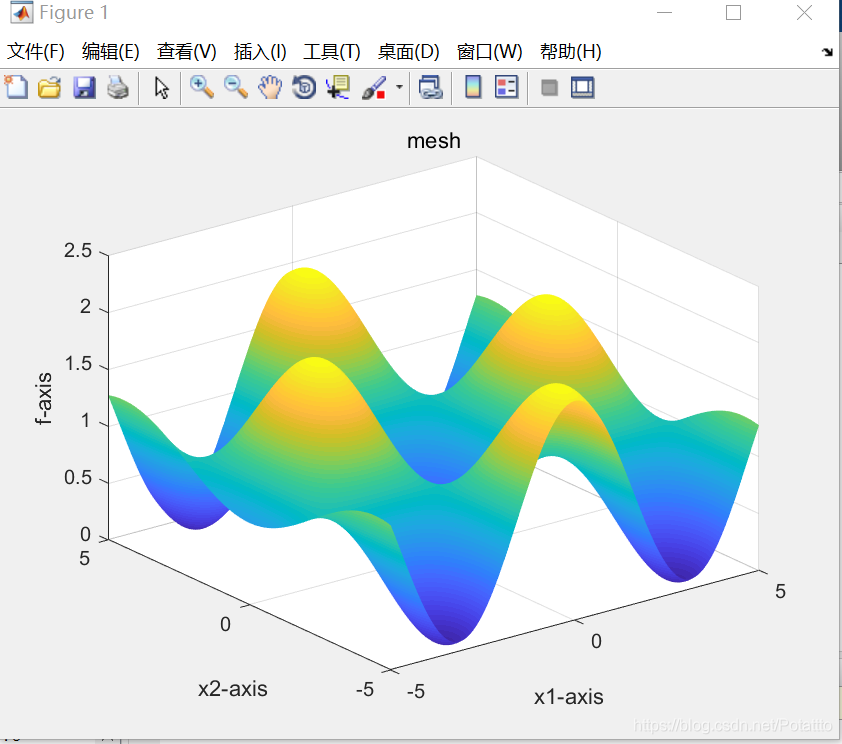
3.对Griewank函数优化
函数代码:
function y=Griewank(x)
%Griewan函数
%输入x,给出相应的y值,在x=(0,0,…,0)处有全局极小点0.
%编制人:
%编制日期:
[row,col]=size(x);
if row>1
error('输入的参数错误');
end
y1=1/4000*sum(x.^2);
y2=1;
for h=1:col
y2=y2*cos(x(h)/sqrt(h));
end
y=y1-y2+1;
%y=-y;
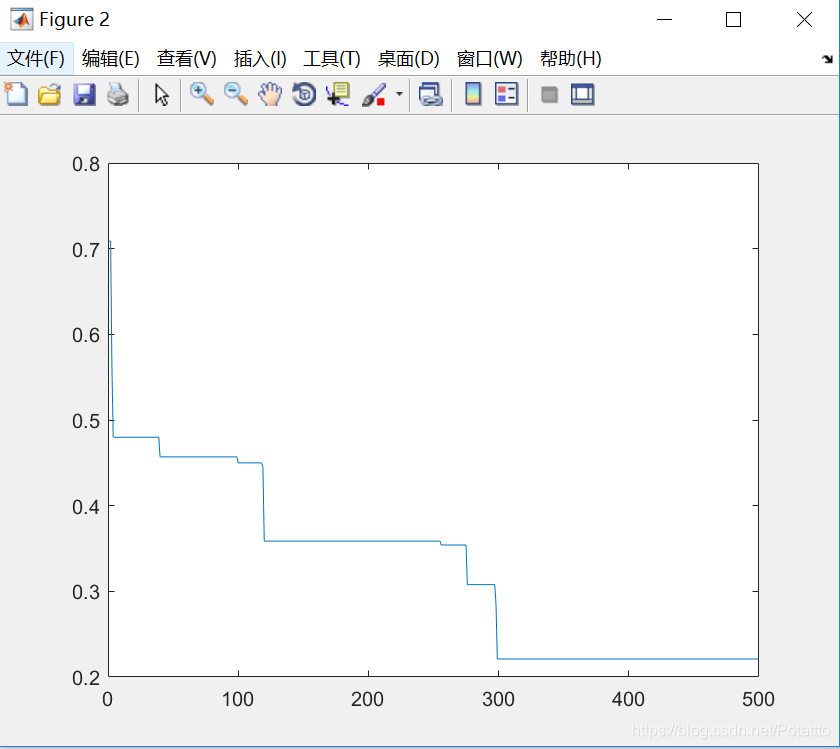
(1)种群数量N=80,维度Dim=5:
bestv =
-0.220954713374530
optxx =
-9.002932551319649 0.087976539589445 -16.041055718475072 -0.087976539589445 -0.615835777126101
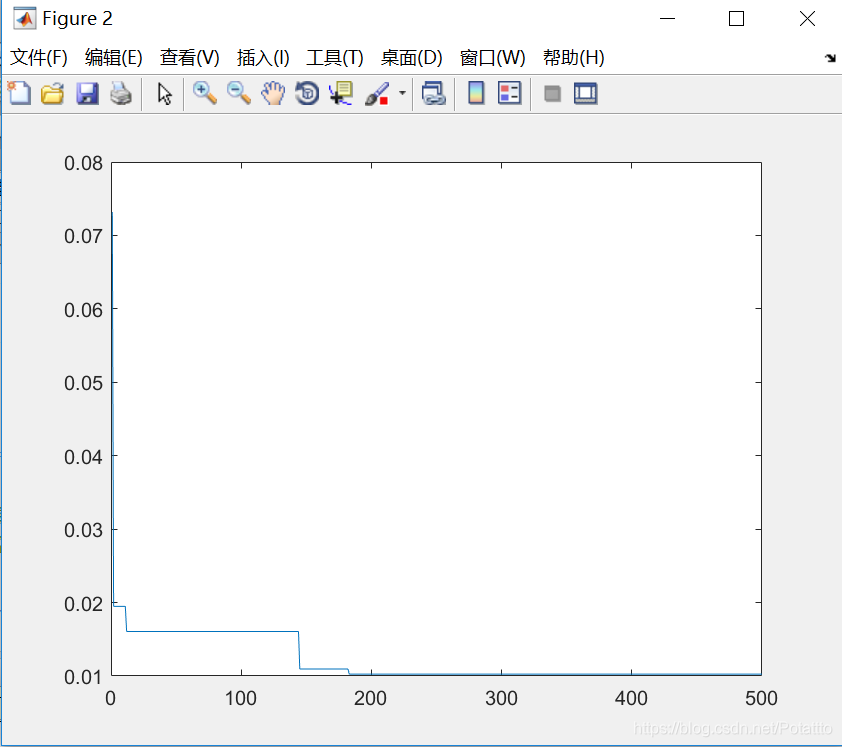
(2)种群数量N=80,维度Dim=2:
bestv =
-0.010262924724034
optxx =
-3.137829912023459 -4.545454545454547
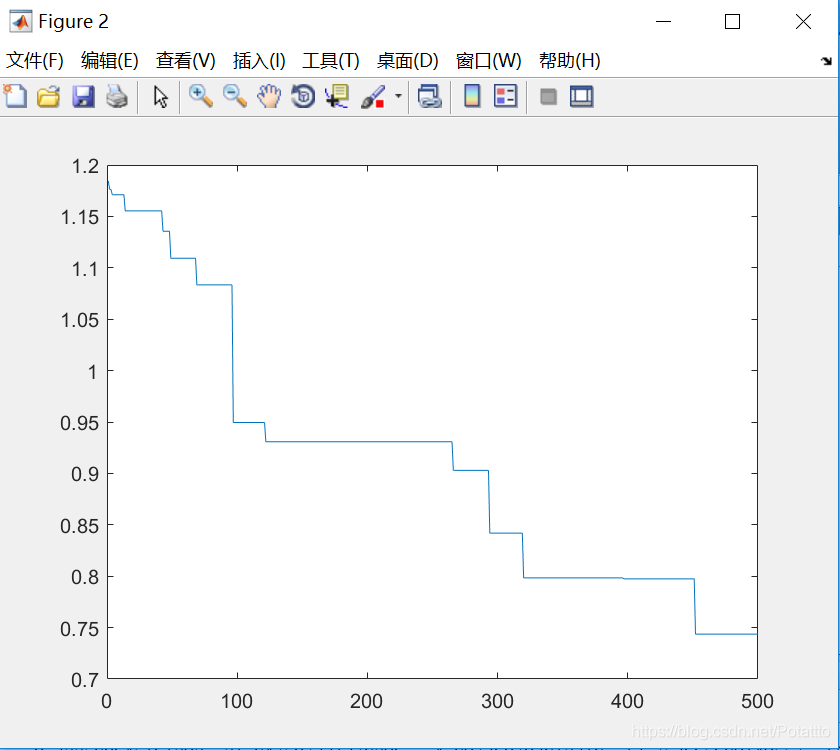
(3)种群数量N=80,维度Dim=10:
bestv =
-0.743678828318803
optxx =
1 至 7 列
3.313782991202345 0.322580645161292 21.847507331378296 -4.897360703812318 13.753665689149557 -14.985337243401759 7.008797653958943
8 至 10 列
-8.123167155425222 8.181818181818180 9.530791788856305
(4)种群数量N=40,维度Dim=5:
bestv =
-0.264051426836767
optxx =
-12.639296187683286 0.381231671554254 15.865102639296190 5.953079178885631 -14.457478005865102
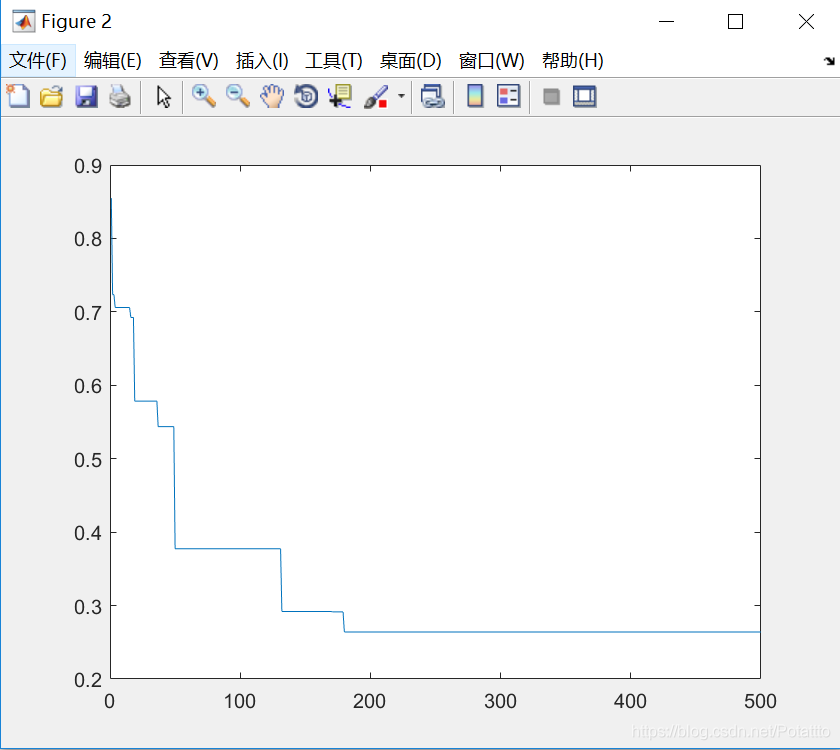
(5)种群数量N=40,维度Dim=2:
bestv =
-0.022366638205714
optxx =
3.137829912023463 4.193548387096776
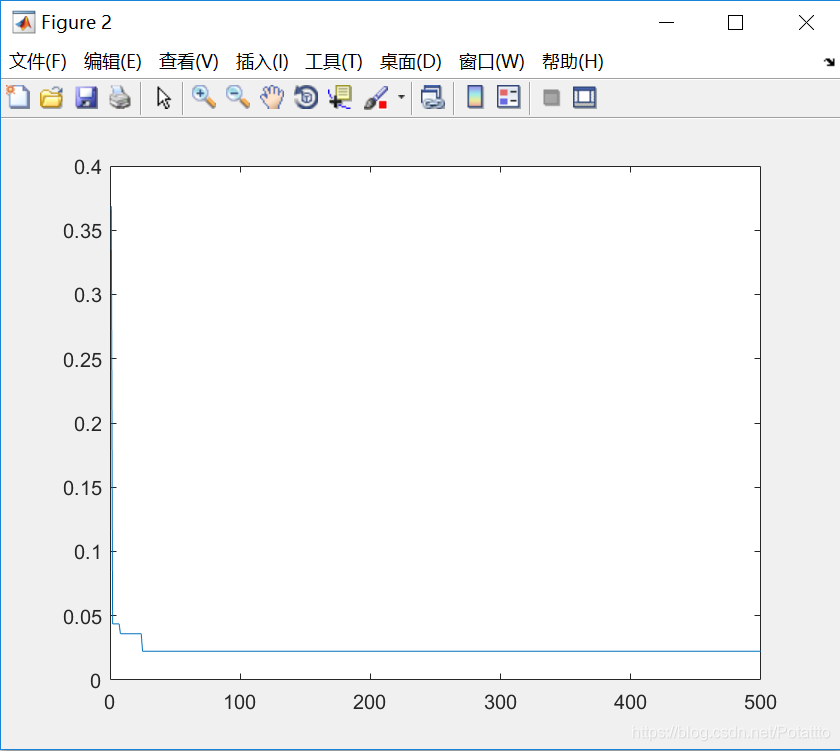
(6)种群数量N=40,维度Dim=10:
bestv =
-0.889135000860089
optxx =
1 至 7 列
-19.325513196480941 12.991202346041057 -1.143695014662757 6.011730205278596 -7.126099706744867 1.143695014662757 9.589442815249264
8 至 10 列
-15.747800586510264 9.413489736070382 -10.175953079178885
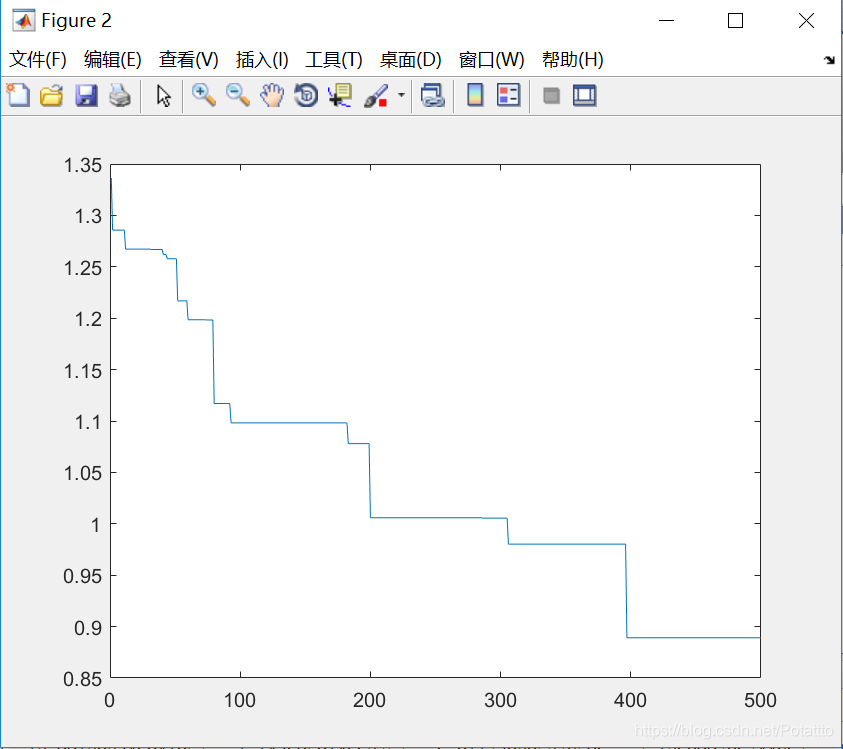
(7)种群数量N=100,维度Dim=5:
bestv =
-0.104165691537920
optxx =
-3.255131964809383 -8.944281524926687 5.366568914956012 -0.322580645161292 -13.812316715542522
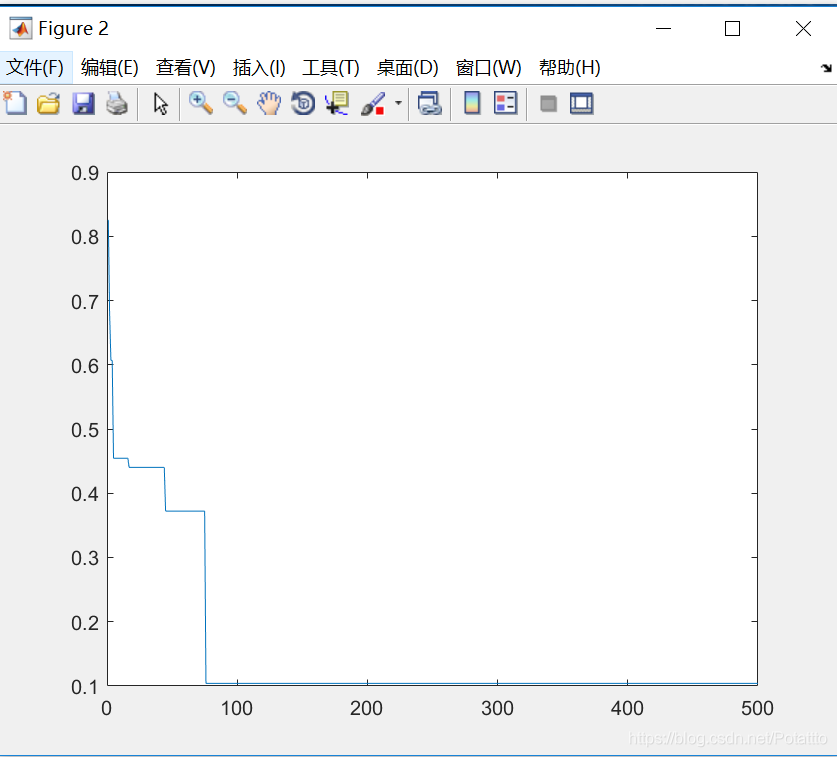
(8)种群数量N=100,维度Dim=2:
bestv =
-0.002365624260429
optxx =
-0.029325513196483 -0.087976539589445
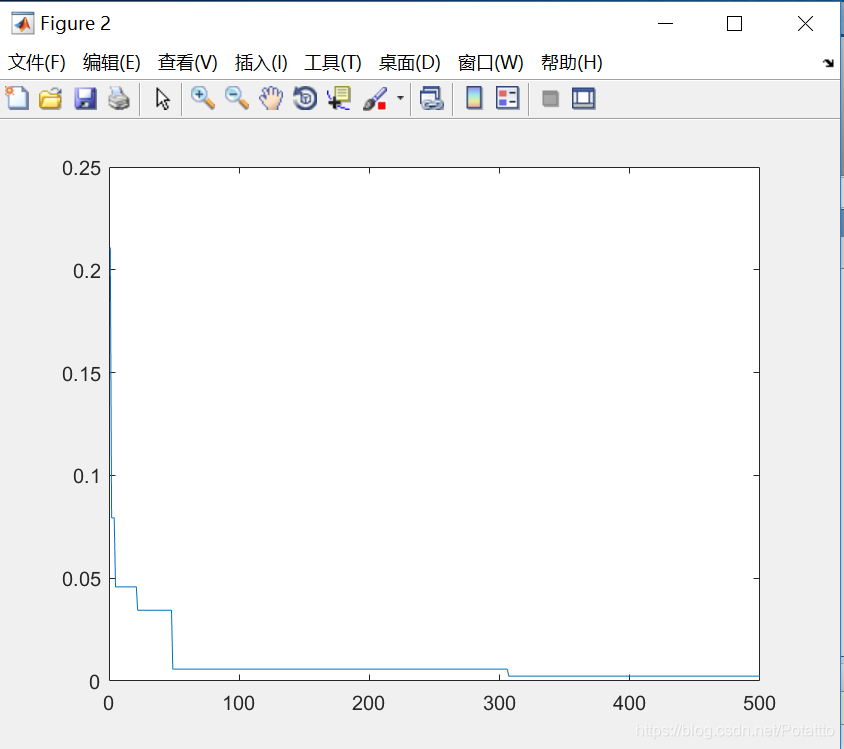
(9)种群数量N=100,维度Dim=10:
bestv =
-0.813898470475840
optxx =
1 至 7 列
3.372434017595310 4.780058651026394 0.205278592375368 0.967741935483872 -5.131964809384165 8.240469208211145 8.357771260997069
8 至 10 列
6.070381231671554 -1.436950146627566 -1.026392961876834
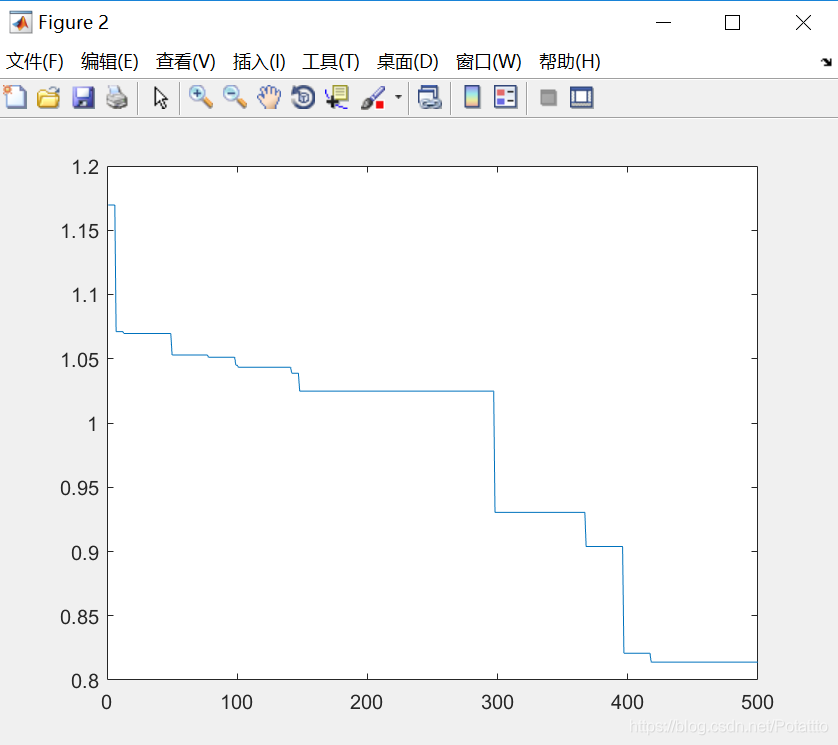
四、结果分析
1.从最优适应度值分析
(1)对于Schaffer函数来说,迭代的次数随着维度增加而增加,但维度变化时最优适应度值变化很小,最优参数较为准确。
(2)对于Rastrigin函数来说,当种群数量N不变时,最优适应度进化曲线已迭代次数随着维度的增加先减少后增加。
(3)对于Griewank函数来说,与Rastrigin函数相反,已迭代的次数随维度的增加先增加后减少,最优参数随维度的增加而减小。
2.从运行所需时间上分析
以函数Griewank为例:
(1)种群数量N=80不变,变化维度
维度Dim=2:
维度Dim=5:
维度Dim=10:
由结果可知:当种群数量不变时,运行时间随着维度的增加而增加。
(2)维度Dim=5不变,变化种群数量N
N=40:
N=80:
N=100:
由结果可知:当维度不变时,运行时间随着种群数量的增加而增加。