每个程序员都曾被前辈告诫过：“代码中不要直接使用double类型做任何算术处理，会存在精度的问题。可以使用JDK中自带的java.math.BigDecimal类处理”。事实也确实如此：
double num1 = 0.1;
double num2 = 0.2;
System.out.println(num1+num2);
/**num1+num2= 0.30000000000000004**/
为什么会如此，浮点类型值的算术计算为什么会存在精度的问题，且听娓娓道来？
计算机存储都是0或者1，二进制表示方式，浮点类型也是如此。但浮点型数值相对于整数的二进制表示更为复杂，存在比如：小数点的精度、数字最大支持范围、存储空间、计算时间等诸多考量。目前计算机的浮点类型采用统一标准为：IEEE754。
什么是IEEE754标准表示法？
数学中常见的10进制数值科学计数法。
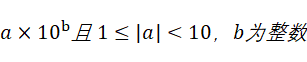。比如：3230000 写为：
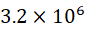。-0.0042 写为：
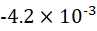。那么用2进制来科学计数方表示可以为：
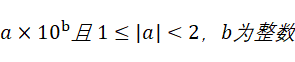。比如6.88 写为：
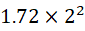，0.05写为：
。
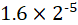实际IEEE754的浮点型实际二进制表示方式：
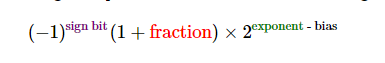
符号位(Sign bit)：假设sign bit为 0，表示为正数，
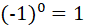。sign bit 为1，表示为负数 ，
。
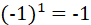1+小数(fraction) ：fraction为科学计数法中的小数部分。如(参考公式二进制转为10进制展示)
exponent-bias : 二进制的科学计数部分，指数部分依据数字的大小可以为正数或者负数。为了精简减去正负的标识，所以添加bias(偏移)常量表示 。对于单精度类型，原始指数范围是：-126到127。bias为127，所以指数范围为1到254。双精度类型，原始指数范围：-1022到1023。当bias为1023 ，指数范围为0到2046。所以实际的指数部分为：power = exponent -bias。
32 bit的单精度float(4字节)类型和64 bit的双精度 double(8字节)类型：
下面是一些特殊情况的表示：
Zero ：Sign 为0，exponent都为0，fraction 都为0；
无穷大：正无穷大Sgin为0，负无穷大Sign为1。exponent都为1，fraction为0；
下面一些IEEE754样例：
单精度的0.085二进制转换过程：
1. 第一步 ：Sign位因为数值为整数所以为0
2. 第二部：
等于
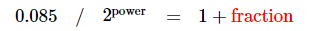
所以
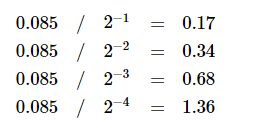
3.对应的指数部分 -4+127=123 对应二进制 01111011.
4.小数部分，0.36乘以2
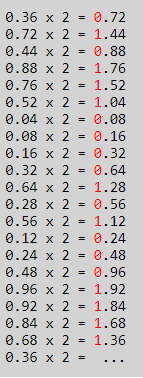
并且出现重复组等，因为小数部分展示只有23位所以二进制为： 01011100001010001111011
最后0.085 的IEEE754格式为： 00111101101011100001010001111011
IEEE754格式转换为10进制转换过程：
二进制值：11000000110110011001100110011010
第一步：Sign为1所以是负数
第二步：exponent 10000001 = 129 减去 bias 127 = 2
第三步：小数部分
所以由以上信息
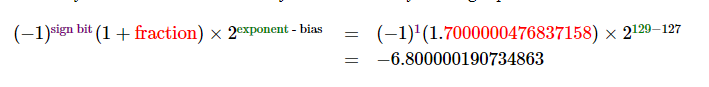
那么示例中的0.1+0.2 是因为在计算机存储浮点类型数据，使用二进制方式。计算机无法精准的存储浮点数，所以直接使用double类型计算会存在精度问题。